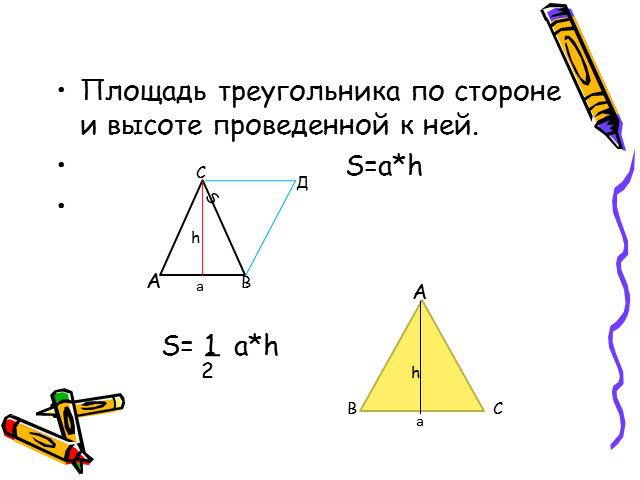
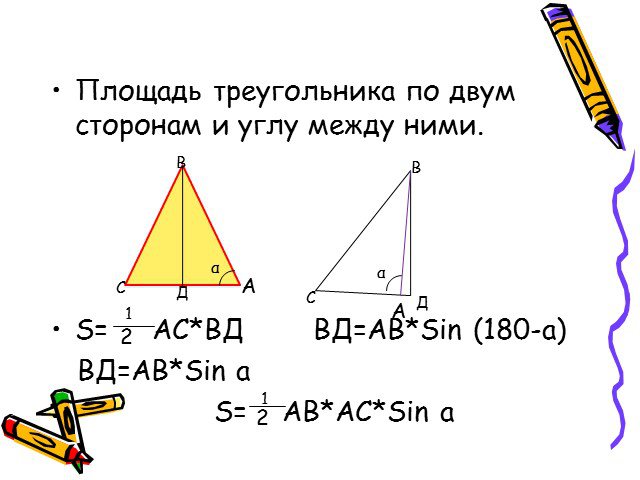
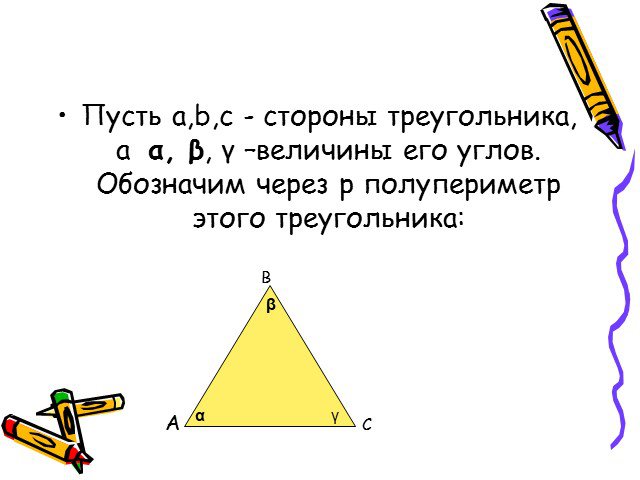
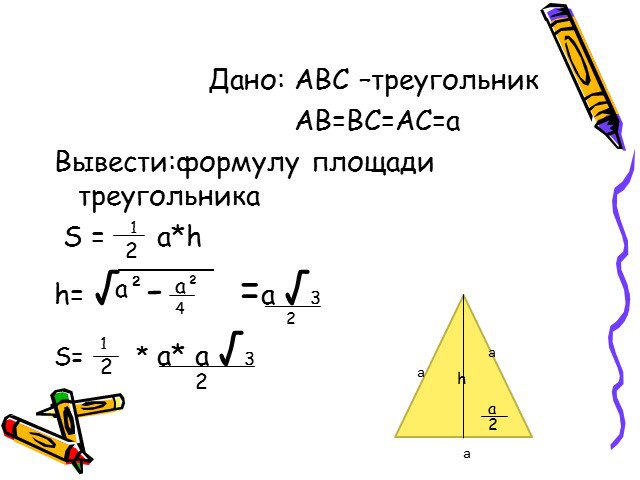
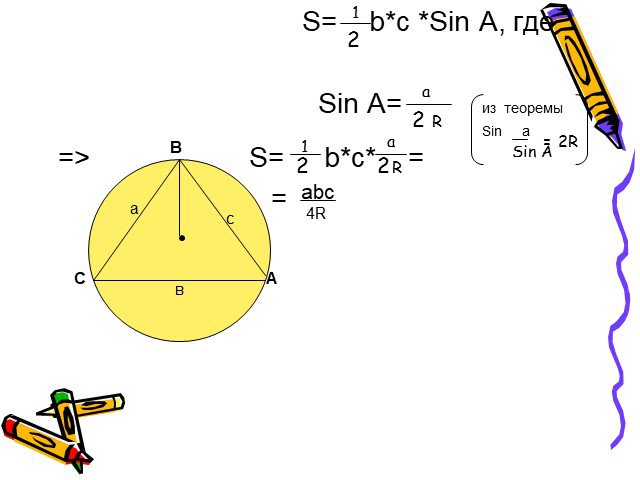
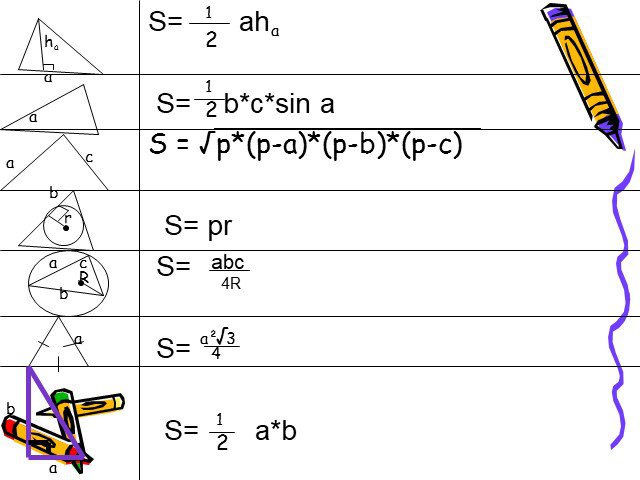
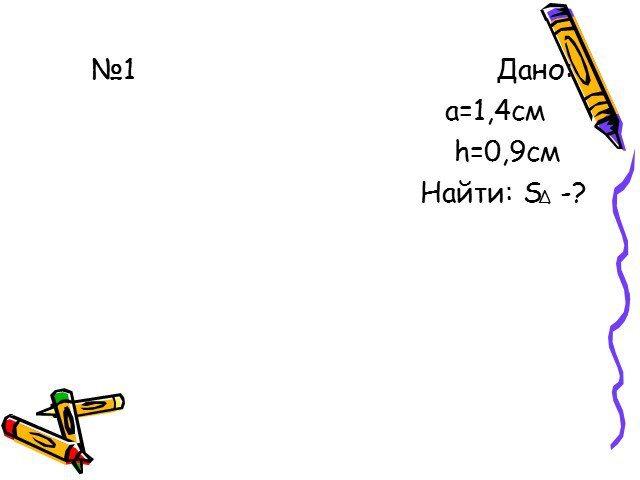
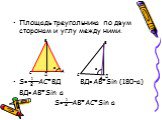
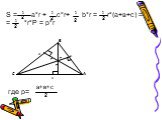
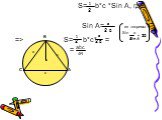
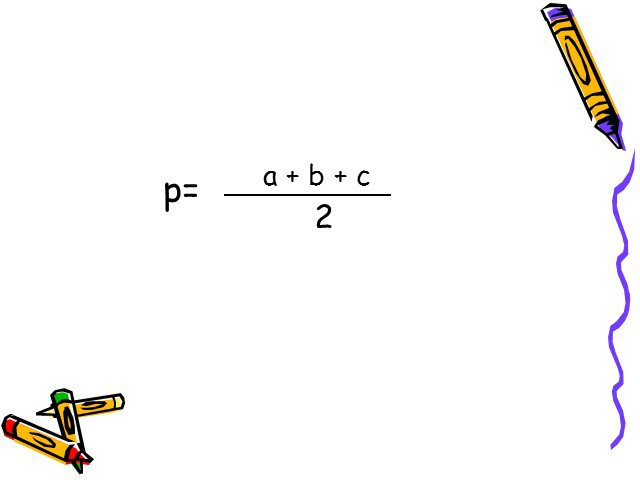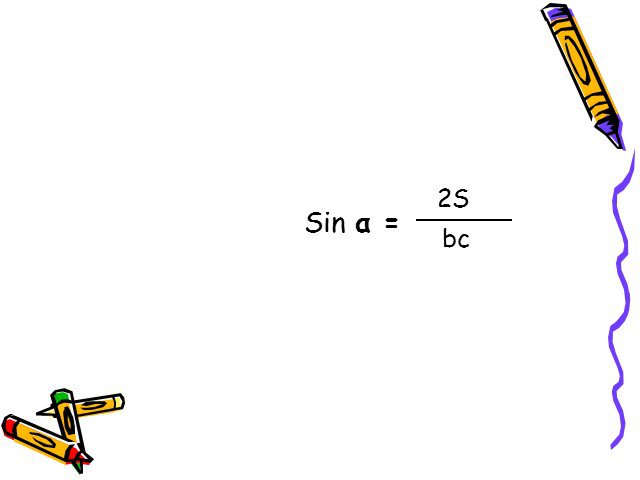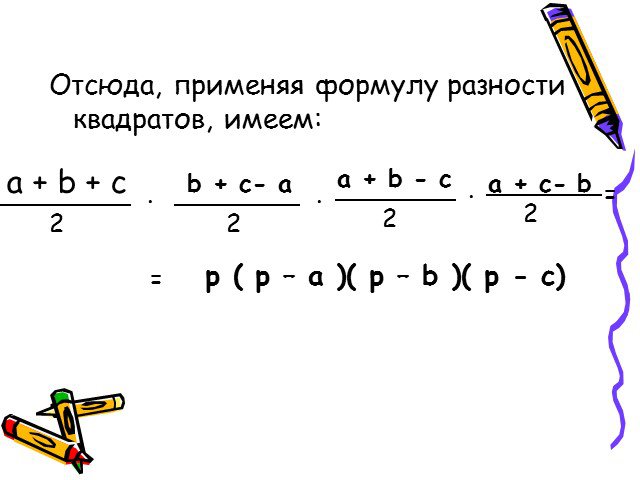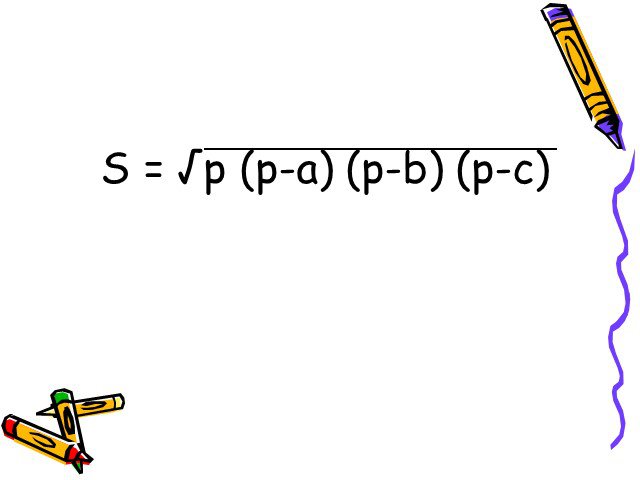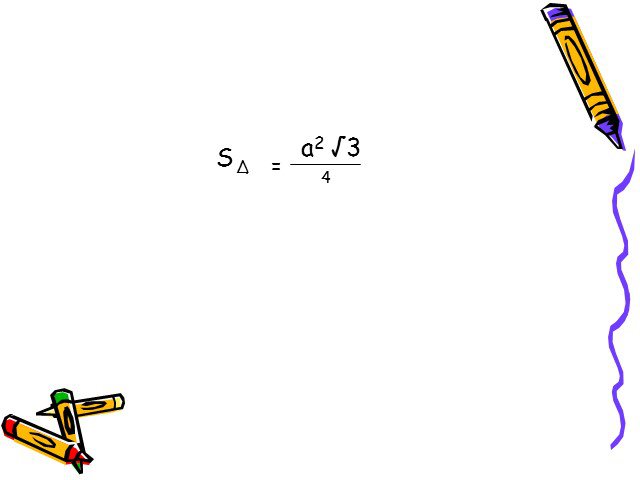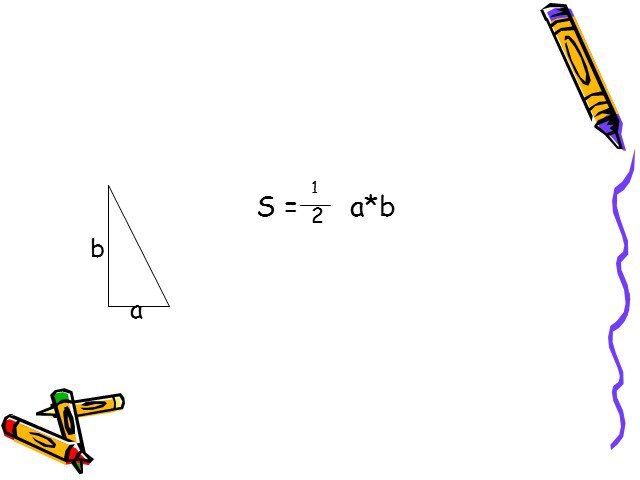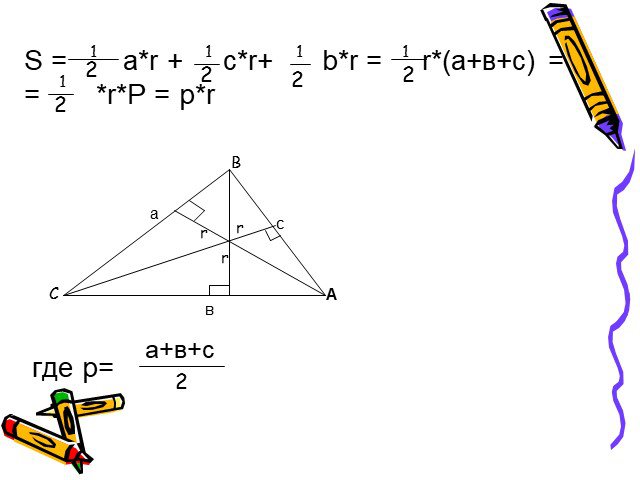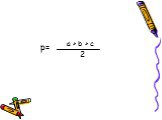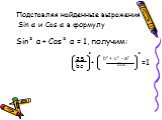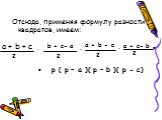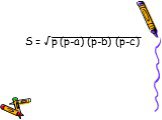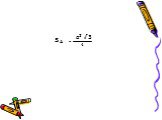Презентация "Формулы для вычисления площади треугольника" по математике – проект, доклад

Скачать презентацию (1.64 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

Слайд 26

Слайд 27

Презентацию на тему "Формулы для вычисления площади треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).

Скачать презентацию (1.64 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Формулы для вычисления площади треугольника 9 класс

Слайд 2

Цель урока: Познакомится с формулами для вычисления площадей треугольника: а) по стороне и высоте, проведенной к этой стороне; б) по двум сторонам и углу между ними; в) формулой Герона г ) Через радиус вписанной окружности и описанной окружности

Слайд 3

Площадь треугольника по стороне и высоте проведенной к ней. S=a*h

А В С Д S h а S= 1 a*h 2

Слайд 4

Площадь треугольника по двум сторонам и углу между ними. S= АС*ВД ВД=АВ*Sin (180-a) ВД=АВ*Sin a S= АВ*АС*Sin a

α 1

Слайд 5

Древнегреческий математик Герон Александрийский (I в. н.э.) Получил формулу для вычисления площади треугольника по его трём сторонам: S = √p (p-a) (p-b) (p-c)

Слайд 6

Краткий вывод формулы Герона

Слайд 7

Пусть a,b,c - стороны треугольника, а α, β, γ –величины его углов. Обозначим через p полупериметр этого треугольника:

β γ

Слайд 8

p= a + b + c

Слайд 9

По теореме косинусов : cos α=

b² +c² – a² 2bc

Слайд 10

Sin α = 2S bc

Слайд 11

Подставляя найденные выражения Sin α и Cos α в формулу

Sin² α + Cos² α = 1, получим:

2S bc ² b² + c² - a² 2bc + =1

Слайд 12

Отсюда, применяя формулу разности квадратов, имеем:

b + c- a a + b - c a + c- b = p ( p – a )( p – b )( p - c)

Слайд 13

S = √p (p-a) (p-b) (p-c)

Слайд 14

Дано: АВС –треугольник АВ=ВС=АС=а Вывести:формулу площади треугольника S = a*h h= √ - =a √3 S= * a* a √3

a a² 4

Слайд 15

∆ a2 √3

Слайд 16

S = a*b b

Слайд 17

S = a*r + c*r+ b*r = r*(а+в+с) = = *r*Р = р*r где p=

в с r а+в+с

Слайд 18

S= b*с *Sin А, где Sin A= из теоремы Sin a => S= b*с* = =

R Sin A 2R аbс 4R

Слайд 19

S= ah S= b*c*sin a S = √p*(p-a)*(p-b)*(p-c) S= pr S= S= S= a*b

c √ 3

Слайд 20

Закрепление

Слайд 21

№1 Дано: а=1,4см h=0,9см Найти: S -?

Слайд 22

№2 Дано: а=5см b=6см α = зо

° Найти: S -?

Слайд 23

№3 Дано: а=5 b=5 с=6

Слайд 24

Д/ З: п.124,125 №30(1), №27

Список похожих презентаций

Решение задач на нахождение площади прямоугольного треугольника

Решить задачи (устно). Р - ? S - ? 12 дм S - ? P = 56 см. P - ? 7 м S = 77 м2 3 см 4 см 6см 13 см = 38 дм R - ? Решить задачу А B C D 2 см = 16 см ...

ПЛАНИМЕТРИЯ: Вычисление площади треугольника

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник. Найдите его площадь в квадратных сантиметрах. Решение 6 Ответ: 6. 9 4 Ответ: ...

Приём вычисления для случаев вида 36 + 2, 36 + 20

Начинается урок, Он пойдёт вам , дети впрок. Постарайтесь всё понять, Чтобы правильно решать. 87 55 69 91. (20 + 5) + 10 (40 + 6) + 20 (60 + 4) + ...

Задачи на вычисление площади треугольника

Девиз урока: «Кто ищет – тот всегда найдет…». Личностные цели. самостоятельно добывать знания, анализировать и обобщать; уверенно и грамотно выражать ...

Презентація « Віршовані задачі для 1 класу»).

Каже мати – квочка: В мене два синочка І чотири дочки. Скільки ж діток в квочки? 2 + 4 = 6. Три веселі киці Грались на травиці. Рижик теж до них прибіг. ...

Применение формул объёма и площади поверхности прямоугольного параллелепипеда

Цель урока: Научиться на практике применять формулы объёма и площади поверхности прямоугольного параллелепипеда. Устный опрос. Сколько ребер у параллелепипеда? ...

Понятие площади

реализовать триединые дидактические задачи: через использование различных уровней обучения. обучение, развитие, воспитание. минимальный, базовый, ...

Построение треугольника по трем сторонам

Цели урока:. Научиться строить треугольник по трем заданным сторонам. Познакомиться с некоторыми ГМТ. Совершенствовать умения по решению задач на ...

Периметр треугольника. Построение треугольника по заданным сторонам

1.Классификация треугольников по длинам сторон. Равносторонний треугольник. 4 см 4см. Разносторонний треугольник. 5см 6 см 7 см. Равнобедренный треугольник. ...

Площадь прямоугольного треугольника

1 3 4. Единицы измерения площадей. За единицы измерения площадей приняты площади квадратов со сторонами, равными единичным отрезкам 1 мм, 1 см, 1 ...

Внетабличное умножение и деление. Приём деления для случаев вида 782, 693

22 января. Классная работа. 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8. Устный счет. 1. А) Уменьшаемое, вычитаемое, разность. Б) Множитель, множитель, произведение. ...

Нейтронная обработка драгоценных и полудрагоценных камней для ювелирной промышленности

Цель: Выяснить, как обрабатывают драгоценные и полудрагоценные камни путём нейтронного и гамма облучения, для ювелирной промышленности. Задачи: 1)Узнать ...

Внеклассное мероприятие по математике для учащихся 6 -ов

Цель внеклассного мероприятия:. 1. Повышение интереса к изучению математики, развитие творческих способностей учащихся и логического мышления. 2. ...

Внеклассное мероприятие по математике для учащихся 6-х классов

“Рыбе – вода, птице – воздух, зверю – лес, степи, горы. А человеку нужна Родина. И охранять природу – значит охранять Родину”. М.М. Пришвин. Наша ...

Внеклассное мероприятие по математике для 8 класса Отличники

1. Способствование проявлению интеллектуальных способностей учащихся. 2. Активизации познавательной деятельности учащихся. 3. Формирование навыков ...

Вневписанная окружность треугольника

Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...

Викторина по математике для 5-6 классов

1.Половина-треть числа. Какое это число? Ответ: 3/2. 2.За книгу заплатили 60 рублей. И ещё 1/3 стоимости книги. Сколько стоит книга? 90 рублей. 3.Как ...

Рабочая программа по математике для 5 класса по УМК И.И. Зубаревой и А.Г. Мордковича

Новые ФГОС. Как обучать? С помощью чего учить? Как проверить достижение новых образовательных результатов? «Основные общеобразовательные программы ...

Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним

Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...

Блок-схема для решения квадратных неравенств

Неравенства второй степени вида. D. D=0 x=m m. D>0 m n. . . . . . . . Нет решения. . . . . . . . . Тренажер. решение квадратных неравенств. Варианты ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.