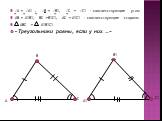
Презентация "Существование треугольника, равного данному" по математике – проект, доклад
Презентацию на тему "Существование треугольника, равного данному" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства треугольника
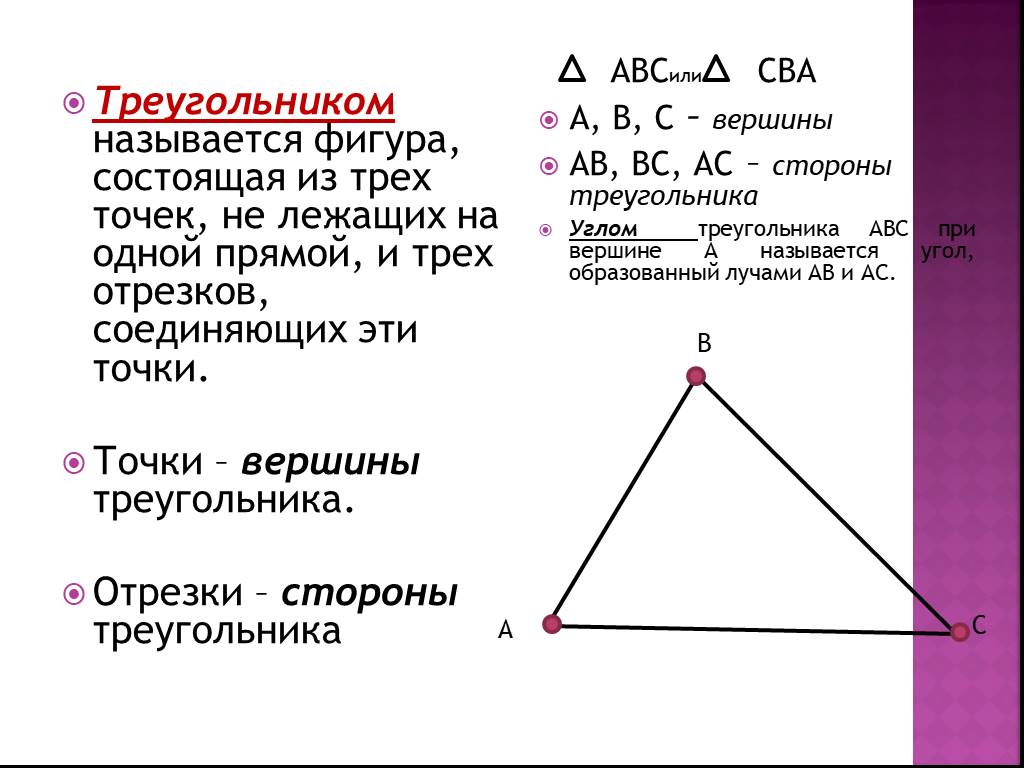
Треугольники Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти ...Соотношения между сторонами и углами прямоугольного треугольника
ОТНОШЕНИЕ ПРОТИВОЛЕЖАЩЕГО КАТЕТА К ГИПОТЕНУЗЕ. ТО, ЧТО ВЫРАЖАЕТ ТЕОРЕМА: «ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО ...Вневписанная окружность треугольника
Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...Свойства равнобедренного треугольника
Теоретический опрос. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Сформулируйте и докажите теорему ...Сумма углов треугольника 2
Цель урока:. Закрепить и проверить знания учащихся по теме «Свойства углов, образованных при пересечении двух параллельных прямых третьей» и «Признаки ...Теорема Пифагора для треугольника
Теорема Пифагора. Легенды и факты о Пифагоре. Авторы презентации : Власенко Д., Белохвостова Т., Слизкова П., Матвеева П., Муравьева А. Пифагорейская ...Геометрия в звездном небе. Свойство углов треугольника
Правила для членов клуба «ПИФАГОР»: Активно знакомиться с геометрическими терминами. 2. Радостно узнавать геометрические фигуры в повседневной жизни. ...Сумма углов треугольника
Цели урока:. 1. Закрепить и проверить знания учащихся по теме : «Свойство углов образованных при пересечении двух параллельных прямых третьей и признаки ...Внешний угол треугольника. Теорема о внешнем угле треугольника
I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...Высота треугольника
Все геометрические фигуры разделить на две группы. Назвать эти группы. Многоугольники. Немногоугольники. пятиугольник четырёхугольник треугольник ...Внешний угол треугольника
Общий вид внешнего угла. Понятие. Свойство внешнего угла. Внешний угол. Внешний угол треугольника. Угол, смежный с каким–нибудь углом треугольника, ...Внешний угол треугольника
Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Соотношения между сторонами и углами треугольника
Теорема о площади треугольников. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Стороны треугольника пропорцианальны ...Задачи на вычисление площади треугольника
Девиз урока: «Кто ищет – тот всегда найдет…». Личностные цели. самостоятельно добывать знания, анализировать и обобщать; уверенно и грамотно выражать ...Средняя линия треугольника
Каким образом эти треугольники поделили на две группы? А B C. Отрезок, соединяющий середины двух сторон, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА. Задача: ...Задачи на неравенство треугольника
Длина любой стороны треугольника не превосходит сумму длин двух других. | AC | ≤ | AB | + | BC |. Следствия из неравенства треугольника. Равенство ...Сумма углов треугольника
Виды углов. Острые Прямые Тупые Развёрнутые Смежные Вертикальные Накрест лежащие Соответственные Односторонние. Сумма углов треугольника. Теорема: ...История треугольника
Что такое треугольник? Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, ...Теорема о пересечении высот треугольника
Цели:. 1) Рассмотреть теорему о точке пересечения высот и следствие из неё; 2) Формировать умения применять известные знания в незнакомой ситуации, ...Конспекты
Конкретно-практическая задача по подбору предмета, равного данному по тяжести
Конспект урока математики в 1 классе по учебнику. . Э.И. Александровой. Тема. : Конкретно-практическая задача по подбору предмета, равного данному ...Конкретно-практическая задача по подбору предмета, равного данному по тяжести
Конспект урока математики в 1 классе. Разработала:. Губарева Ю.М.,. . учитель начальных классов. МОУ СОШ №125. г.Волгограда. Тема. ...Построение отрезка, равного данному, с помощью циркуля и линейки
МБОУ «Бетькинская средняя общеобразовательная школа». Тукаевского муниципального района РТ. Урок математики. в 4в классе на тему:. ...Сумма углов треугольника
Урок по геометрии в 7 классена тему: «Сумма углов треугольника». Тип урока:. урок изучения нового материала.Цели урока:. Образовательные:. доказать ...Сумма углов треугольника
Муниципальное казенное общеобразовательное. . учреждение лицей №11. Открытый урок в 7 классе по теме:. Сумма углов треугольника. Подготовила ...Сумма углов треугольника
ПЛАН-КОНСПЕКТ УРОКА Сумма углов треугольника. . . ФИО (полностью). . Нагорнова Елена Владимировна. . . . . Место работы. . ...Сумма углов треугольника
Методический портал учителя «Методсовет» - http. ://. metodsovet. . su. . Автор: Морина Светлана Алексеевна. Учитель математики МБОУ СОШ ...Соотношения между сторонами и углами треугольника
Общеобразовательная школа I. -III. ступеней №31. Симферопольского городского совета. Республики Крым. Обобщающий урок. по теме. «Соотношения ...Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника (8-й класс). Цели:. Совершенствовать. навыки решения прямоугольных треугольников. ...Синус, косинус, тангенс. Площадь треугольника
Автор: Чичерова Татьяна Ивановна. Место работы: МОУ «Образцовская СОШ». Должность: учитель математики. . . Урок геометрии в 9 классе. Тема: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 мая 2019
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию