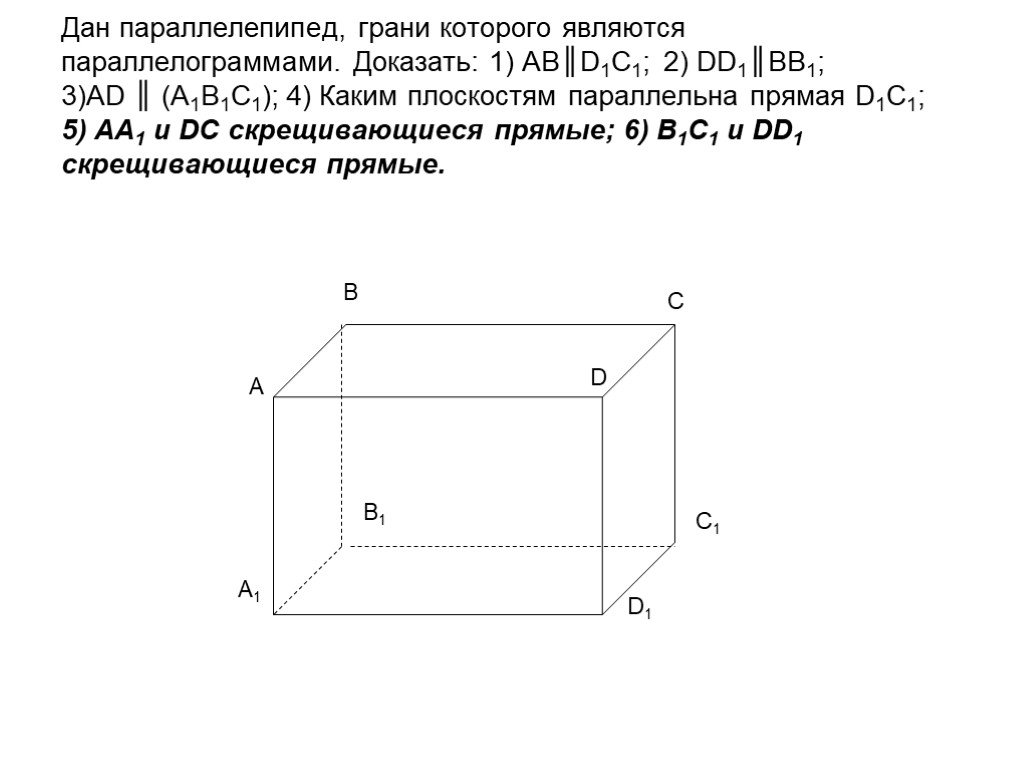
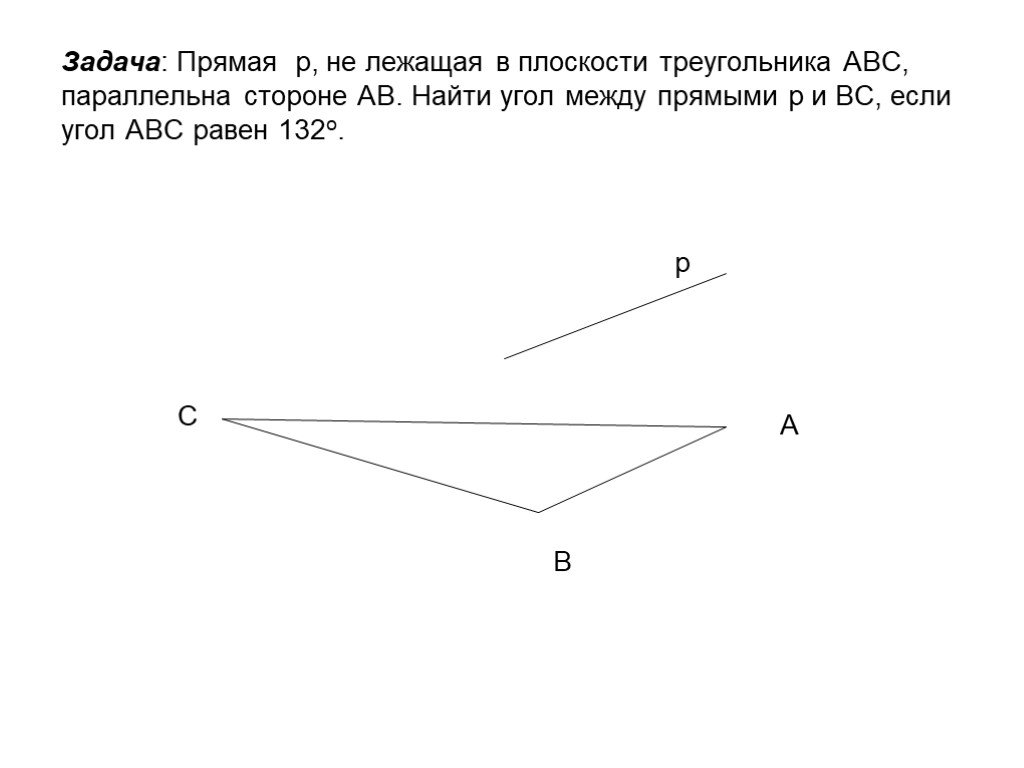
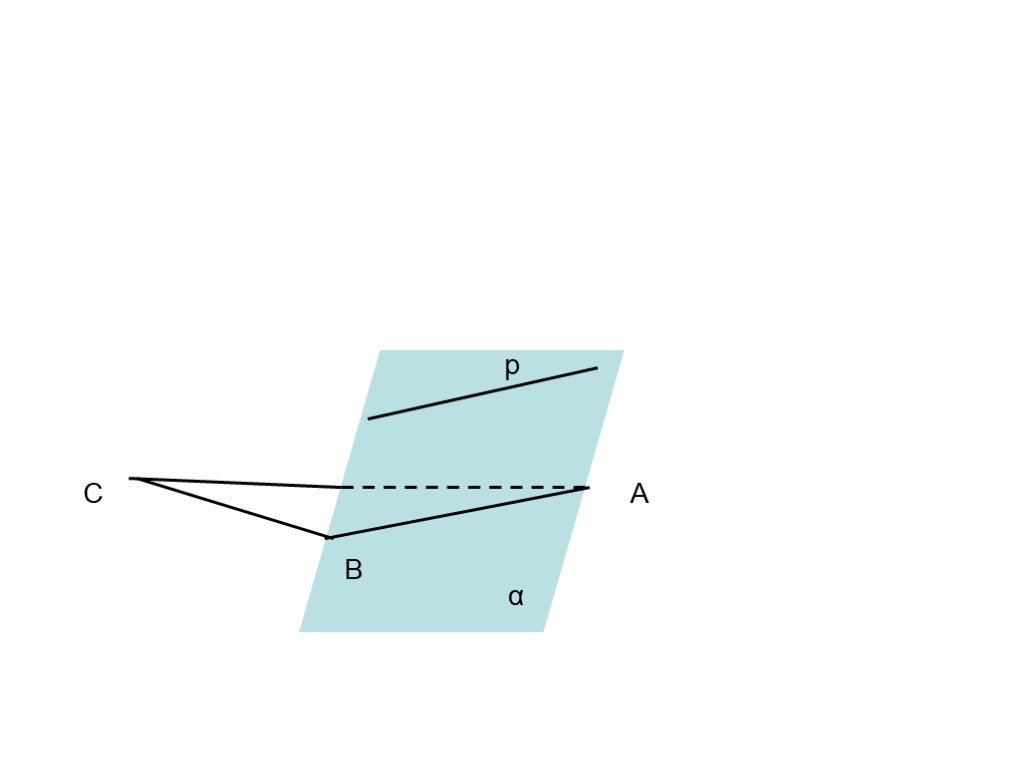
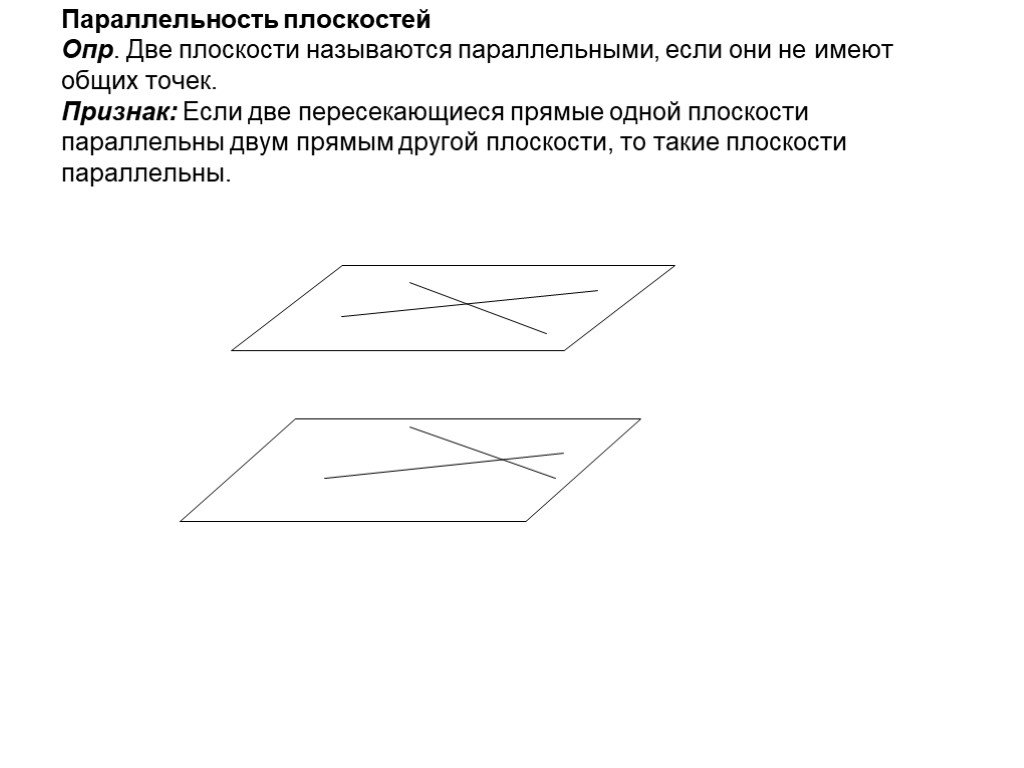
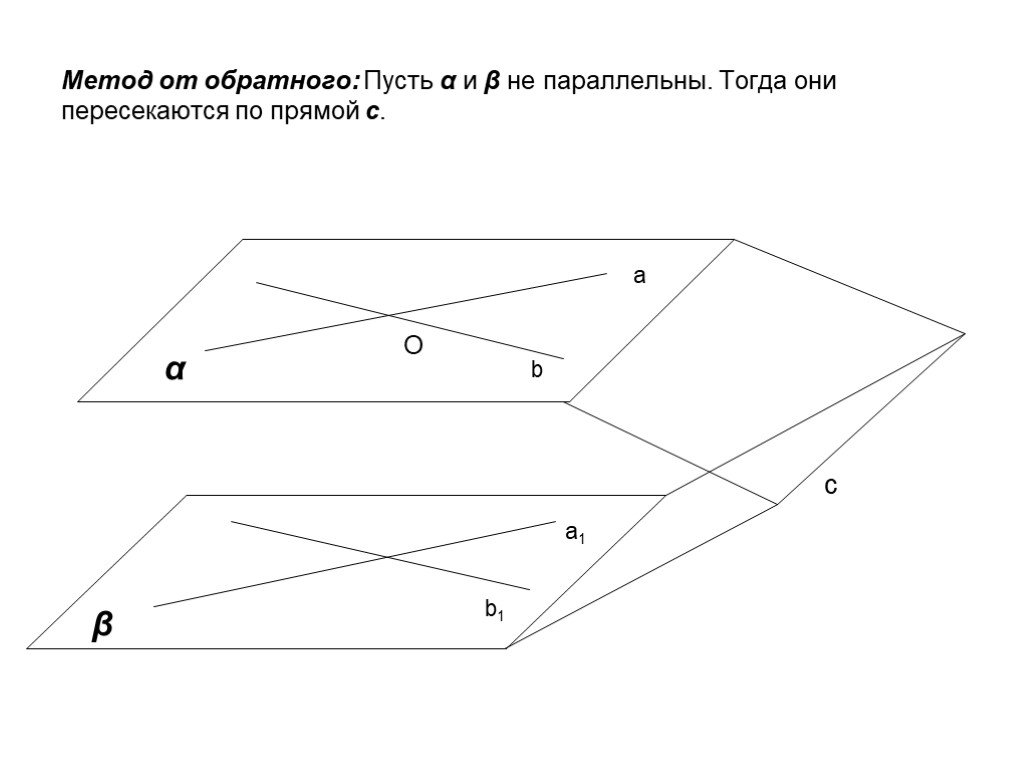
Презентация "Определение параллельности прямых" по математике – проект, доклад
Презентацию на тему "Определение параллельности прямых" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Признаки параллельности прямых. Свойства параллельных прямых
. УСТАНОВИТЕ СООТВЕТСТВИЕ:. 2 и 3 накрест лежащие 7 и 4 5 и 7 соответственные 5 и 4 3 и 4 односторонние 4 и 8 1 и 4 вертикальные 1 и 3 7 и 3 смежные ...Устные упражнения на уроках геометрии. Признаки параллельности прямых
Ответ. . . . . . . . . . ...Признаки параллельности прямых
а в а) б) в) г) д) с е). На каком рисунке прямые пересекаются ? Пересекающиеся прямые имеют: а) не имеют общих точек; б) одну общую точку. . Две прямые ...Признаки параллельности прямых
Добрый день! Меня зовут Умняша . Я сегодня буду Вашим помощником. Хочу познакомить Вас с миром геометрии. И проверить, как вы умеете решать задачи ...Признаки параллельности прямых
а b c 1 8 7 6 5 4 3. Накрест лежащие. Односторонние. 2 Соответственные. Назови углы. ∠1=32° Дано: ∠2=32° Доказать: a b ∥. ∠1=48° ∠2=132°. ∠1=47° ∠2=133°. ...Признаки параллельности прямых
Признаки параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2. Если при пересечении ...Признаки параллельности прямых
Ход урока. 1. Организационный момент. 2. Решение тестовых заданий с последующим обсуждением. 3. Проверка ответов теста. 4. Изучение нового материала. ...Признаки параллельности двух прямых
1 3. Назовите основные геометрические фигуры. 4 5. Как могут располагаться на плоскости две прямых относительно друг друга? а b aIIb 2 а) б) c с - ...Признаки параллельности двух прямых
1. Отметь знаком «+» правильные утверждения и знаком «-» — ошибочные. 1. Параллельными прямыми называются прямые, которые не пересекаются. 2. Параллельными ...Признаки параллельности прямых
D А В С 1. о 2 4. Х У О Р 3. Е Н. 35 0 70 К. . ...Определение параллельных прямых
ЦЕЛИ УРОКА:. Ввести понятие параллельных прямых; Секущей прямой; Накрест лежащих углов; Односторонних углов; Соответственных углов; Научится определять ...Определение параллельных прямых
. . . Составьте конспект п. 24. Вопрос Какие прямые называются параллельными? Изобразите и обозначьте параллельные прямые Какие отрезки называются ...Признак параллельности прямых
«Дорогу осилит идущий а геометрию мыслящий». Цель урока:. Закрепить знания видов углов, образованных в результате пересечения двух прямых секущей. ...Что мы знаем о параллельности
Урок построен в виде игры. За основу взяты правила игры «Кто хочет стать миллионером?». Можно воспользоваться тремя подсказками по 1 разу: 50 : 50 ...Аксиома параллельных прямых
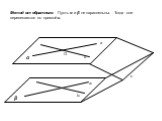
Аксио́ма – исходное утверждение, принимаемое истинным без доказательств, и которое в последующем служит «фундаментом» для построения какой-либо теории, ...Параллельность прямых и плоскостей - зачет
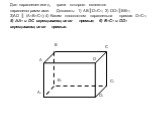
Цели урока:. Повторить теоретический материал главы «Параллельность прямых и плоскостей». Проверить усвоение темы в ходе зачета. Формирование у учащихся ...Перпендикулярность прямых и плоскостей
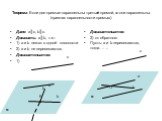
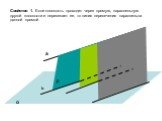
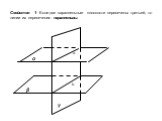
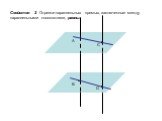
Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Теорема 3.1 Если две пересекающие прямые параллельны ...Определение эллипса
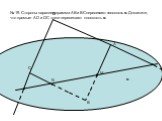
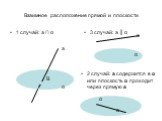
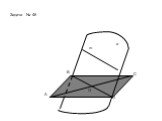
Определение эллипса. Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F1, F2 есть величина постоянная, называется ...Определение вероятности
При классическом определении вероятность события определяется равенством Р(А) = m/n, где m – число элементарных исходов испытания, благоприятствующих ...Определение квадратного уравнения. Неполные квадратные уравнения
Решите уравнения Х=±2 Х=± Корней нет Х=0 Х=0,Х=2. 5х-2=0. Разделите данные уравнения на две группы. Какие уравнения называются квадратными? 1. Уравнение ...Конспекты
Признаки параллельности прямых
". Признаки параллельности прямых". Цель урока:. • Закрепить знания учащимися видов углов, образованных в результате пересечения двух прямых секущей; ...Признаки параллельности прямых. Урок 2. Материалы урока
Свечникова Л.С. Урок «Признаки параллельности прямых». МБОУ «Средняя общеобразовательная школа №2 им. А.И. Исаевой» г. Нефтеюганска ХМАО-Югра. . ...Признаки параллельности прямых
Касибаева Жибек Айтжановна. . Учитель физики и математики. Школа - гимназия имени Батыр Баяна города Булаево. . Района Магжана Жумабаева. ...Признаки параллельности прямых
«Урок с использованием информационно-коммуникационных технологий». Почебутова Лариса Ильинична, учитель математики, МОУ СОШ №3 г. Усть-Кут Иркутской ...Параллельные прямые. Признаки параллельности прямых
Урок. по геометрии для 7 класса. «Параллельные прямые. Признаки параллельности прямых». Урок проведён в 7 «В» классе. . в рамках недели ...Признаки параллельности прямых
Конспект урока по геометрии к конкурсу « Лучший урок с использованием ИКТ». УМК:. Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и другие. «Геометрия ...Признаки параллельности двух прямых
Мишукова Любовь Алексеевна. . Тема урока: Признаки параллельности двух прямых. Тип урока:. Урок закрепления и применения полученных знаний на практике. ...Определение числа глагола. Изменение глаголов по числам
Русский язык (3-й класс). Тема: «Определение числа глагола. Изменение глаголов по числам». Учитель начальных классов:. ...Определение четырёхугольника
Тема урока: Определение четырёхугольника. Цели:. Образовательная –. ввести понятие о четырёхугольнике и его элементах, научить отличать выпуклый ...Аксиома параллельных прямых
Открытый урок геометрии в 7 классе. Тема урока: «Аксиома параллельных прямых». Дата проведения урока: 16 января 2014 года. Учитель: Олейникова ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 марта 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию