Презентация "Декартово произведение" по математике – проект, доклад

Скачать презентацию (0.48 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Презентацию на тему "Декартово произведение" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 7 слайд(ов).

Скачать презентацию (0.48 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Выполнили: Индюшкина Ольга, Салимова Ксения.

ПРЕЗЕНТАЦИЯ НА ТЕМУ: «ДЕКАРТОВО ПРОИЗВЕДЕНИЕ»

Слайд 2

Декартовым произведением множеств А и В называется множество пар, первые элементы которых принадлежат множеству А, вторые – множеству В. Обозначают АXВ. Таким образом, АXВ = {(x;y) | xЄA, yЄB}.

Слайд 3

Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

Слайд 4

Рассмотрим следующий пример. Известно, что АXВ={(2, 3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)}. Установим, из каких элементов состоят множества А и В. Так как первый элемент пары декартового произведения принадлежит множеству А, а второй – множеству В, то данные множества имеют следующий вид: А={2, 3}, B={3, 5, 6}.

Слайд 5

Количество пар в декартовом произведении АXВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АXВ)=n(A)Xn(B).

Слайд 6

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента. Используя понятие кортежа, можно определить понятие декартового произведения n множеств.

Слайд 7

Декартовым произведением множеств А1, А2, …, Аn называют множество кортежей длины n, образованных так, что первый элемент принадлежит множеству А1, второй – А2, …, n-ый – множеству Аn. Пример: Пусть даны множества А={2, 3}; В={3, 4, 5}; С={7, 8}. Декартово произведение АXВXС={ (2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7), (2, 5, 8), (3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)}.

Список похожих презентаций

Скалярное произведение векторов в координатах

Проверка домашнего задания. №1039(в,г) А В С D O 900 №1040(г). №1042(а,б) a. Повторение. Назовите координаты вектора. (3;-1). Найдите координаты суммы ...

Угол между векторами и скалярное произведение векторов

Скалярное произведение векторов. Скалярным произведением векторов называется произведение длин этих векторов на косинус угла между ними. Свойства ...

Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Числа называют скалярами. ...

Скалярное произведение векторов

Вектор – направленный отрезок. Направление вектора указывается стрелочкой. Векторы обозначают латинскими буквами , а так же. Длина вектора a(x, y):. ...

Скалярное произведение векторов

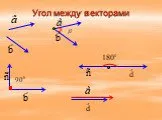
Угол между векторами. Пусть a и b – два данных вектора. Отложим от произвольной точки О векторы ОА = a и ОВ=b. Если векторы a и b не сонаправленные ...

Скалярное произведение векторов

?.?? ред. А.В. Ефимов, Б.П. Демидович Линейная алгебра и основы математического анализа / В.А. Болгов, Б.П. Демидович, А.В. Ефимов [и др.]. - М.: ...

Скалярное произведение вектора

Физический смысл. Скалярное произведение векторов имеет простой физический смысл и связывает работу A, производимую постоянной силой при перемещении ...

Скалярное произведение векторов

Скалярное произведение в координатах

1. Сформулируйте теорему синусов. 2. Сформулируйте теорему косинусов. 3. Что значит «решить треугольник»? 4. Какое наименьшее число элементов надо ...

Скалярное произведение в координатах

Теорема. В прямоугольной системе координат скалярное произведение векторов выражается формулой. Доказательство. По теореме косинусов: АВ²=АО²+ВО²-2АО·ВО·соsα. ...

Скалярное произведение

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ. Для скалярного произведения векторов справедливы свойства, аналогичные свойствам произведения чисел: 1. 2. 3. Используя ...

Векторное произведение двух векторов

Цели и задачи. Цели: Рассмотреть основные понятия по теме «Векторное произведение двух векторов» Задачи: Ввести понятие векторного произведения двух ...

«Скалярное произведение векторов» геометрия

Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.