Презентация "Алгоритмы на графах: определение наличия циклов в графе" по информатике – проект, доклад
Презентацию на тему "Алгоритмы на графах: определение наличия циклов в графе" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгоритмы в нашей жизни
МОУ « Тучковская средняя общеобразовательная школа № 2». Цели урока «Алгоритмы в нашей жизни»: Привить навыки составления алгоритмов. Показать способы ...Алгоритмы сжатия. Алгоритм построения орграфа Хаффмана
Давид Хаффман (1925-1999) Давид начал свою научную карьеру студентом в Массачусетсом технологическом институте (MIT), где построил свои коды в начале ...Алгоритмы в нашей жизни
В обычной жизни. Каждый из нас, не задумываясь, использует множество различных алгоритмов. Я задумался:. Где мы с ним встречаемся? Что же такое алгоритм? ...Алгоритмы на примере среды программирования «Паркетчик»
Строка меню «Паркетчик». Основные команды паркетчика. Пример:. Программа { положить(к); Шаг вправо; положить(к); Шаг вправо; положить(к); }. Команды ...Алгоритмы
Алгоритм. Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (в 825 году) ученый из города Хорезма Абдулла (или Абу Джафар) ...Алгоритмы
6 2 из 6 5 4 3 1. Как слепить снеговика. Алгоритм – это описание конечной последовательности шагов в решении задачи, приводящей от исходных данных ...Влияние компьютерных игр на психику подростков
Интернет – Важнейшее достижение человечества. Цель работы:. Выявить особенности влияния интернет-игр на психику подростков. Поставленные задачи. 1. ...Влияние социальных сетей на подростков
Предыстория. Чтобы получить 50 миллионов пользователей радио потребовалось 40 лет Телевидению – 10 лет Интернету – 4 года iPod – 3 года Социальная ...Влияние компьютера и компьютерных игр на здоровье и психику человека
Первая экспериментальная группа:. Вторая экспериментальная группа:. Выводы:. большинство детей и подростков отдают свое предпочтение музыкальным и ...Влияние компьютера на психику человека
Психологические симптомы человека, относящегося к группе риска интернет- зависимых людей:. - хорошее самочувствие или эйфория за компьютером; - невозможность ...Алгоритмы
Алгоритм. Происхождение слова «алгоритм» связано с именем великого математика Мухаммеда аль-Хорезми. Перу этого учёного принадлежит книга по математике, ...Анимация на VBA
Автор презентации «Анимация на VB6» Помаскин Юрий Иванович - учитель информатики МБОУ СОШ№5 г. Кимовска Тульской области. Презентация сделана как ...Алгоритмы
Определение исполнитель. Исполнитель – это некоторый объект (человек, группа людей, животное, техническое устройство), способный выполнять определенный ...Алгоритмы
1. Выбрать команду Файл → Сохранить как. 2. В открывшемся окне выбрать нужную папку. 3. В поле «Имя» указать имя файла. 4. Нажать кнопку «Сохранить». ...Алгоритмы
Исправьте алгоритм «Поездка в гости». Выйти из дома. Выйти из автобуса. Сесть в автобус № 10. Дойти до автобусной остановки. Проехать 3 остановки. ...Алгоритмы
Робик. Команды для Робика. Привет, я робот Робик. Поле Робика Границы поля Стенки Позиция Робика. Закрашенная клетка. Робик всегда закрашивает клетку, ...Алгоритмы
Понятие алгоритма. Алгоритм – это строгая и четкая последовательность действий, выполнение которых приводит к определенному результату. Требования ...Алгоритмы симметричного шифрования
Криптография. Основные понятия. Рассмотрим общую схему симметричной, или традиционной, криптографии. Рис. 2.1. Общая схема симметричного шифрования. ...Алгоритмы
Вспоминать Развивать Проверять. Нарисуй фигуру Начало 2. 2 3 4 5 2 2. Приготовь какао. возьми чашку положи ложку какао в чашку начало возьми молоко ...Анализ отклика на случайное воздействие в MSC
Раздел 14. Анализ отклика на случайное воздействие. ТИПЫ ДИНАМИЧЕСКИХ ПРОЦЕССОВ………………………………… 14 - 4 АНАЛИЗ ОТКЛИКА НА СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ..……...…….. ...Конспекты
Алгоритмы сжатия. Алгоритм построения орграфа Хаффмана
. План-конспект занятия по информатике. Город:. . Раменское. МОУ «СОШ № 8». Учитель:. . Константинова Елена Ивановна. Класс:. . 11 «А». ...Алгоритмы на паскале
ПЛАН-КОНСПЕКТ УРОКА «Название». ФИО Бурзаев Андрей Игоревич. . Место работы МБОУ СОШ №1 им. М.Горького г. Арзамас. . . . Должность. ...Информационные модели на графах
Урок "Информационные модели на графах". Цели урока:. . •расширить представления учащихся о видах информационных моделей;. . •сформировать ...Алгоритмы в нашей жизни
Тема:. Алгоритмы в нашей жизни. Тип урока:. урок - объяснение. Цели урока:. Образовательные:. Формирование умения грамотно излагать свою ...Графика на языке программирования АВС Pascal
ПЛАН-КОНСПЕКТ УРОКА. ТЕМА: «. Графика на языке программирования АВС. Pascal. ». Тип урока:. получение. новых знаний. Технология:. системно-деятельностный ...Влияние компьютерных игр на формирование агрессивных моделей поведения учащихся начальных классов
Конспект урока в 4 классе. на тему:. «Влияние компьютерных игр на формирование агрессивных моделей поведения учащихся начальных классов». Выполнила: ...Алгоритмы
ЧАСТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА «КРИСТАЛЛ» ГОРОДА СЫЗРАНЬ САМАРСКОЙ ОБЛАСТИ. Конспект итогового ...Алгоритмы с повторениями
Технологическая карта. . . Тема урока:. Алгоритмы с повторениями. . Тип урока:. урок изучения и закрепления новых знаний. Разработан:. ...Линейное программирование на языке TurboPascal
Интегрированный урок информатика и экология 7 классе. Тема урока : Линейное программирование на языке TurboPascal. Цель:. . Сформировать навыки ...Исследование зависимости мощности потребляемой лампочкой накаливания от напряжения на ее зажимах
Интегративный урок по физике и информатике. Преподаватель информатики и физики Искакова Гайни Каратаевна. Костанайский гуманитарный колледж. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Информатика
Автор презентации:Югов Иван Олегович
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию




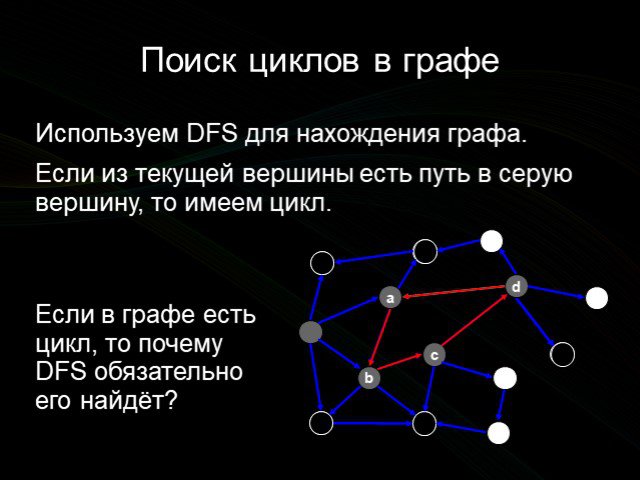
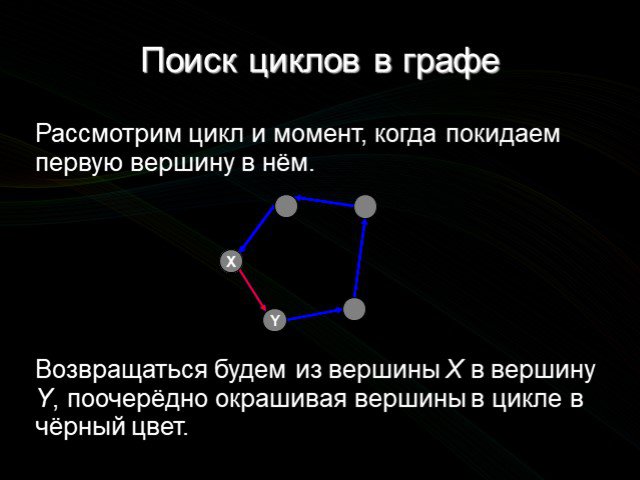









![Как определить сам цикл? Сделаем стек. При заходе в вершину помещаем её в стек, при выходе — забираем её оттуда. массив stack длины n — стек вершин; sp — указатель вершины стека (число элементов в нём). Pascal sp := 0; Push(v): Inc(sp); stack[sp] := v; Pop: Dec(sp); C sp = 0; Push(v): stack[++sp - 1 Как определить сам цикл? Сделаем стек. При заходе в вершину помещаем её в стек, при выходе — забираем её оттуда. массив stack длины n — стек вершин; sp — указатель вершины стека (число элементов в нём). Pascal sp := 0; Push(v): Inc(sp); stack[sp] := v; Pop: Dec(sp); C sp = 0; Push(v): stack[++sp - 1](https://prezentacii.org/upload/cloud/14/09/3678/images/thumbs/screen6.jpg)
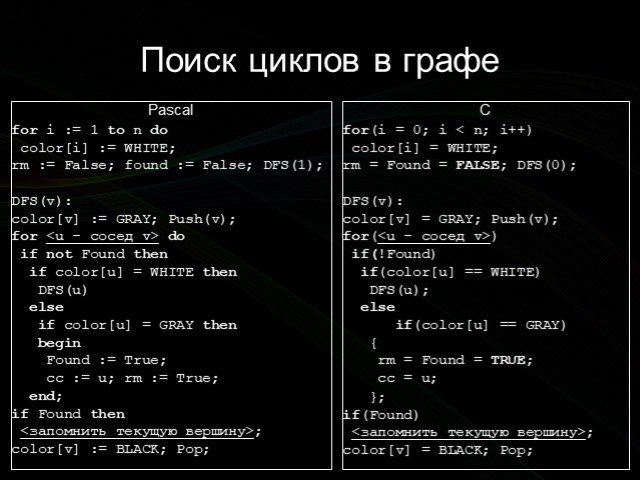
![Pascal for i := 1 to n do color[i] := WHITE; rm := False; found := False; DFS(1); DFS(v): color[v] := GRAY; Push(v); for do if not Found then if color[u] = WHITE then DFS(u) else if color[u] = GRAY then begin Found := True; cc := u; rm := True; end; if Found then ; color[v] := BLACK; Pop;. C for(i Pascal for i := 1 to n do color[i] := WHITE; rm := False; found := False; DFS(1); DFS(v): color[v] := GRAY; Push(v); for do if not Found then if color[u] = WHITE then DFS(u) else if color[u] = GRAY then begin Found := True; cc := u; rm := True; end; if Found then ; color[v] := BLACK; Pop;. C for(i](https://prezentacii.org/upload/cloud/14/09/3678/images/thumbs/screen7.jpg)

































