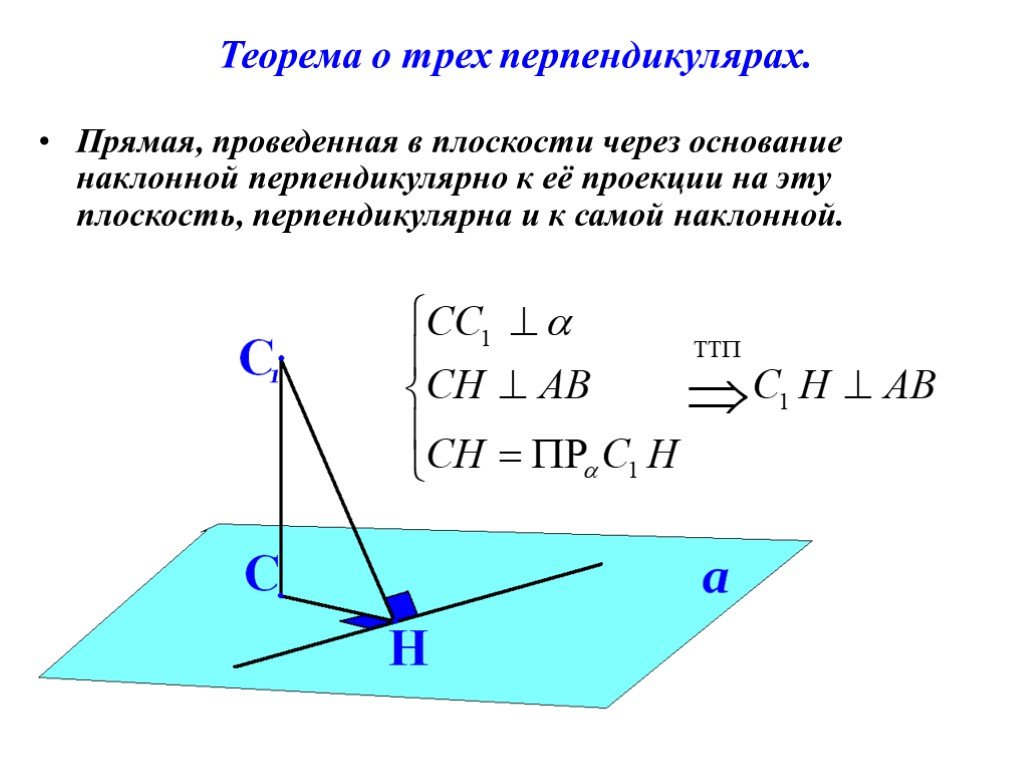
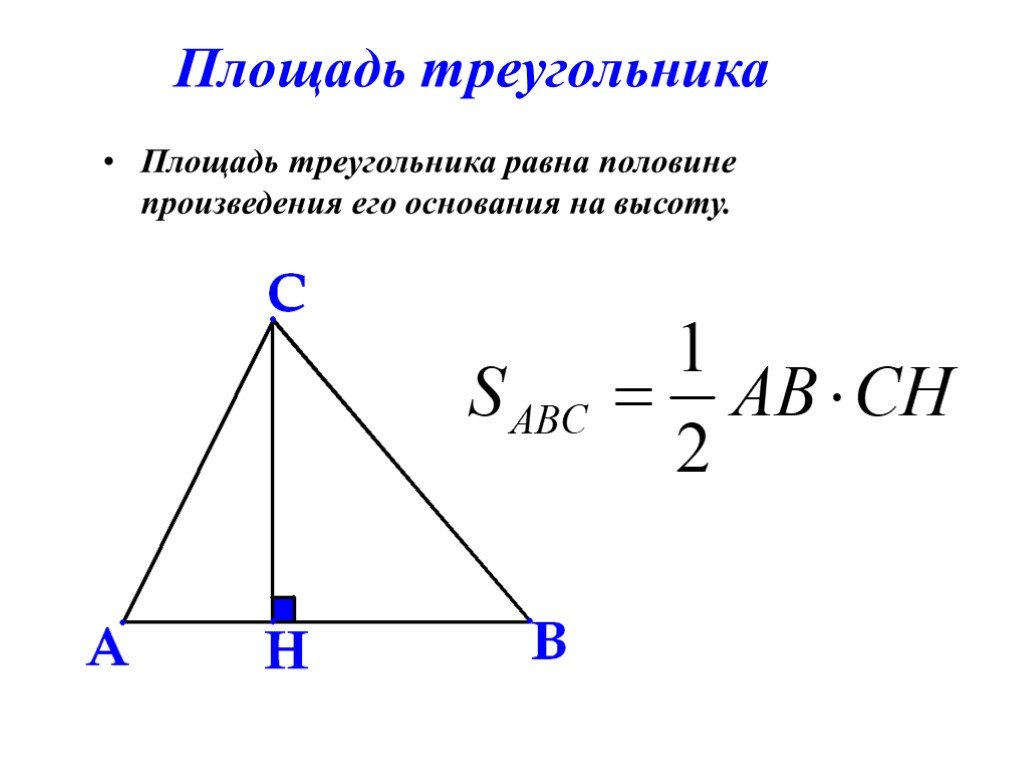
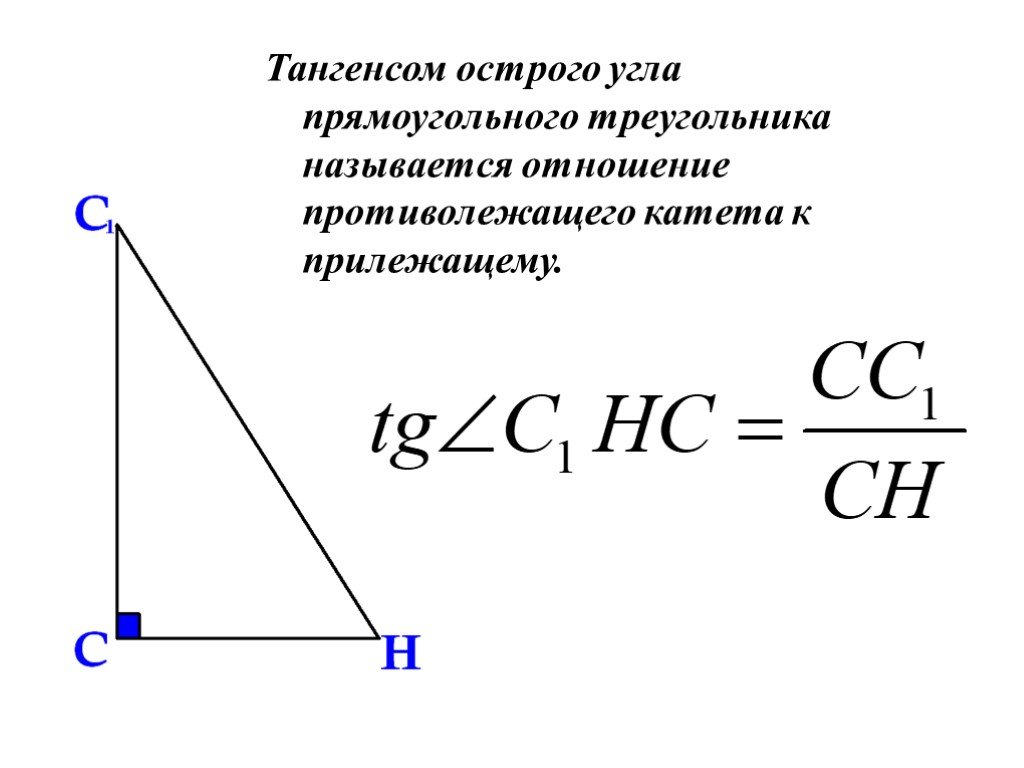
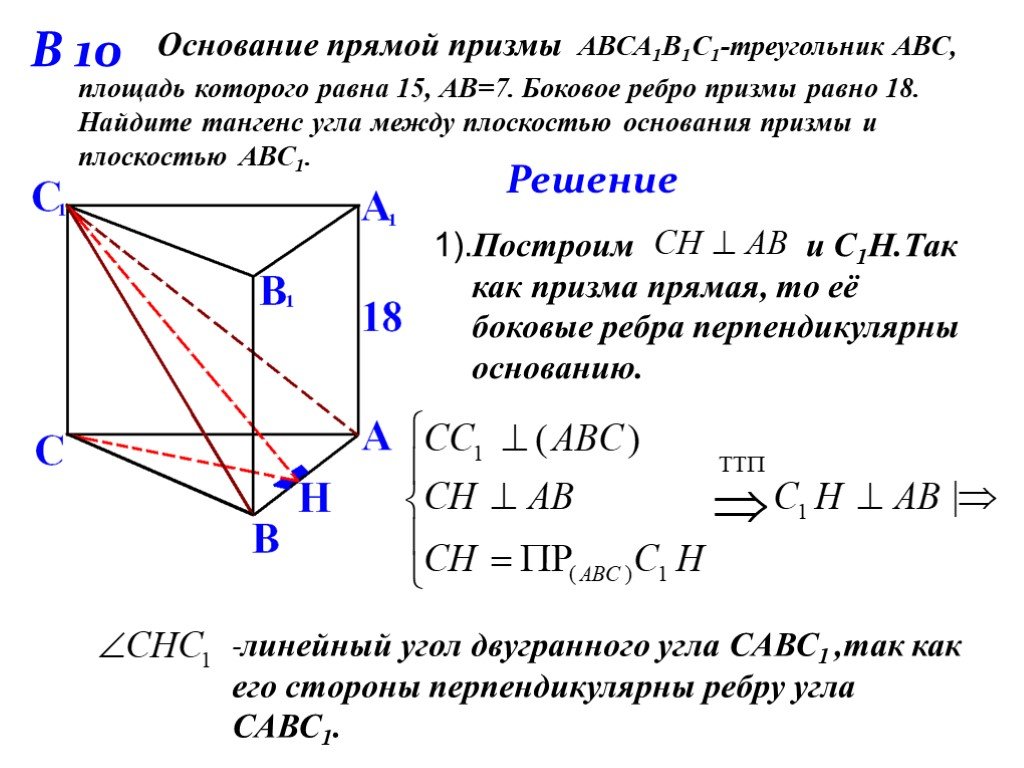
Презентация "Подготовка к ЕГЭ" – проект, доклад
Презентацию на тему "Подготовка к ЕГЭ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: ЕГЭ и ГИА. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Морфология Подготовка к ЕГЭ
Имя существительное Имя прилагательное Имя числительное Местоимение Глагол Причастие и деепричастие Наречие Служебные части речи Типичные ошибки. ...Обобщение изученного материала. Подготовка к ЕГЭ
Цели урока. Учебные. 1.Обобщить изученный материал на примере частей Б, С. 2. Проверить меру готовности обучающихся к сдаче ЕГЭ. Развивающие. 1. Развитие ...Подготовка к ЕГЭ
ИНТЕРНЕТ-РЕСУРСЫ для участников ЕГЭ в Центре оценки качества образования по вопросу организации и проведения ЕГЭ в крае: - на информационном сайте ...Подготовка к ЕГЭ
Какой из перечисленных городов является наибольшим по численности населения? 1) Тюмень 2) Новосибирск 3) Архангельск 4) Хабаровск. 2) Новосибирск. ...Подготовка к ЕГЭ
Отсутствие навыков тестирования; Ошибочное понимание формулировок в тестовых заданиях ЕГЭ; Неправильное распределение времени на выполнение заданий; ...Подготовка к ЕГЭ
В1. 1)Набор стаканов стоит 250 руб. Какое наибольшее число наборов можно купить на 2000 руб. во вре- мя распродожи,когда скидка соста- вит 30%? 2)Клиент ...Подготовка к ЕГЭ - анализ поэтического текста
Б. Пастернак ФЕВРАЛЬ, ДОСТАТЬ ЧЕРНИЛ И ПЛАКАТЬ…. Февраль. Достать чернил и плакать! Писать о феврале навзрыд, Пока грохочущая слякоть Весною черною ...Подготовка к ЕГЭ - письмо
1. Обращения, пожелания. Liebe Tina Lieber Herr Schneider Hallo Jan Sehr geehrter Herr Frei Hey Julia Ich gratuliere Dir… Ich wunsche Dir…. 2. Основные ...Подготовка к ЕГЭ 2012
В6. найдите площадь треугольника АВС , считая стороны квадратных клеток равными 1. 03.04.2018. Яковлева М.С. МОУ"СОШ №10 им. В.П.Поляничко. г. Магнитогорска. ...Подготовка к ЕГЭ рекомендации обучающимся- участникам ЕГЭ 2012 года, учителям и родителям по совместной подготовке к итоговой аттестации
Принципиальная особенность подготовки к ЕГЭ. Совместная, коллективная работа школы и учителя, выпускника и его родителей по подготовке к экзамену: ...Подготовка к ЕГЭ и предметным олимпиадам
Название проекта- Подготовка к ЕГЭ и предметным олимпиадам. Тренажер «Чтение графиков» Предметная область Математика. Участники (возраст, класс) : ...Подготовка специалистов, обеспечивающих организацию и проведение ЕГЭ в 2012 году
Обучение руководителей ППЭ. Нормативно-правовые документы, регламентирующие порядок и процедуру проведения государственной (итоговой) аттестации обучающихся, ...Подготовка к экзаменационной работе в форме ЕГЭ
Задания 1- 4 1. Какая общая мысль объединяет прочитанный и прослушанный тексты? Есенин производил впечатление скромного и застенчивого юноши. Есенин ...Подготовка и проведение ЕГЭ в ППЭ
Глава II. СИСТЕМА ОБРАЗОВАНИЯ Статья 15. Общие требования к организации образовательного процесса п. 4. … Государственная (итоговая) аттестация обучающихся, ...Онлайн-подготовка к ЕГЭ
Дата старта проекта. Октябрь 2011. Идея. Тестоник – это путь к максимальным баллам на едином государственном экзамене (ЕГЭ). http://bit.ly/szcBcp. ...Содержание индивидуального пакета участника ЕГЭ
Объединение бланков ЕГЭ в Федеральном Центре тестирования. Федеральный центр тестирования. Общие принципы заполнения полей бланков ЕГЭ. Все бланки ...СИСТЕМА ПОДГОТОВКИ К ЕГЭ В ВЫПУСКНОМ КЛАССЕ
Система подготовки к ЕГЭ состоит из следующих составляющих:. 1) Повторение изученных литературоведческих терминов. Система подготовки к ЕГЭ состоит ...Вероятность получения положительной оценки при сдаче ЕГЭ, путем угадывания правильного ответа.
Цель:. Провести исследование по определению вероятности получения положительной оценки при сдаче ЕГЭ путем угадывания правильного ответа. А. Н. Колмогоров. ...ЕГЭ 2011
Успеваемость по русскому языку на ЕРЭ в Верхнеуральском районе. Оценки ЕРЭ в 2010 году по русскому языку. Рейтинг школ по среднему баллу (русский ...Особенности заполнения бланков ЕГЭ
Правила заполнения бланка № 1 Участник заполняет регистрационную часть бланка; Математика. Литература – часть А не заполняют. Оставляют чистой; Краткий ...Конспекты
Подготовка к итоговой контрольной работе. Повторение
«Науку все глубже постигнуть стремись. Познанием вечного жаждой томись,. Лишь первых познаний блеснет тебе свет,. Узнаешь: предела для знания нет». ...Подготовка к празднику День Матери
Департамент образования администрации г. Липецка. Муниципальное автономное образовательное учреждение дополнительного образования детей. . ...Подготовка к ГИА
Родительское собрание в 9 классе. Тема: «Подготовка к ГИА(ОГЭ) ». Классный руководитель Гордеева А.А. На собрание приглашены завуч школы и ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2018
Категория:ЕГЭ и ГИА
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию