М-2, часть 1

Урок 4.

Тип урока: ОНЗ.

Тема: «Взаимное расположение прямых».

Авторы: Мазурина С.Е., Куракина Н.М. (НОУ «Школа Сотрудничества», г. Москва).

Основные цели:

1) Сформировать представление о взаимном расположении прямых на плоскости, о способе нахождения точки пересечения прямых, о параллельных прямых.

2) Тренировать умение изображать точки и прямые, анализировать и решать составные задачи на нахождение целого, преобразованию единиц измерения длины.

Мыслительные операции, необходимые на этапе проектирования: сравнение, анализ, классификация.

Демонстрационный материал:

1) геометрические фигуры из цветной бумаги, на которых маркером проведены отрезки:

;

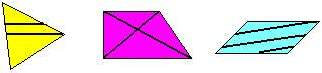
2

пересекающиеся

непересекающиеся

параллельные

) карточки со словами:

, , ;

3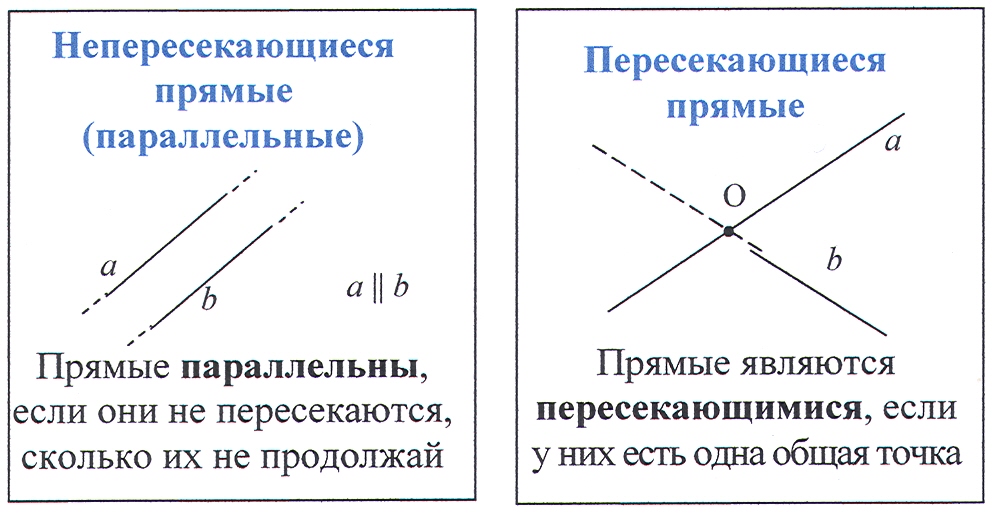) карточки с опорными сигналами:

Раздаточный материал:

1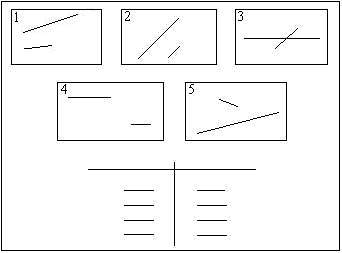) карточка с заданием для пробного действия (на листе А–4):

2) чистые листы А–4 на каждого.

Ход урока

1. Мотивация (самоопределение) к учебной деятельности:

Цель:

1) актуализировать требования к ученику со стороны учебной деятельности;

2) создать условия для возникновения у учащихся потребности включения в учебную деятельность через создание доброжелательной атмосферы в классе;

3) установить тематические рамки урока: точка и прямая.

Организация учебного процесса на этапе 1:

– Чему вы учитесь на любом уроке? (Мы учимся учиться.)

– Напомните, что это значит? (Учиться – это понять, чего я не знаю, и самому построить способ.)

– С какими фигурами вы работали на прошлом уроке? (С отрезком, точкой, прямой, кривой линией.)

– В какой раздел математики вы заглянули? (В геометрию.)

– Сегодня урок тоже будет посвящён точке и прямой, а значит, вы опять пойдёте в страну … (Геометрию).

– И вновь узнаете что-то новое. А с каким настроением ходят в гости? (С хорошим.)

– Я надеюсь, что у вас тоже хорошее настроение?

– Тогда вы смело можете отправиться в гости. Жители геометрии ждут вас!

2. Актуализация и пробное учебное действие.

Цель:

1) актуализировать представление о точке и прямой, их взаимном расположении;

2) тренировать умение обозначать точки и прямые латинскими буквами;

3) тренировать мыслительные операции: анализ, сравнение, обобщение, классификацию;

4) актуализировать норму пробного действия;

5) организовать выполнение учащимися индивидуального задания для пробного действия;

6) организовать фиксацию учащимися возникшего затруднения в выполнении пробного действия или его обосновании.

Организация учебного процесса на этапе 2:

1) Актуализация представлений о точке и прямой, тренинг мыслительных операций.

Открыть фигуры на доске:

;

– Назовите фигуры, которые вы видите на доске. (Треугольник, четырёхугольники, отрезки, точки.)

– Среди других фигур вы назвали отрезки. Скажите, чем похожи, и чем отличаются прямая и отрезок? (Похожи тем, что это прямые линии, но отрезок ограничен с двух сторон, а прямая – нет: её можно продолжать в обе стороны сколько угодно.)

– Какую фигуру можно назвать «лишней»? Почему? (Треугольник – так как у него три угла, а у остальных фигур – четыре. Четырёхугольник посередине – так как внутри него есть пересекающиеся отрезки, а внутри других – отрезки не пересекаются. Четырёхугольник справа – так как внутри него есть три отрезка, а внутри остальных фигур – два.)

2) Обозначение точек и прямых, их взаимное расположение.

Открыть чертёж на доске:

– Посмотрите на чертёж. Какие линии вы видите на чертеже? (Прямые.)

– Что вы можете сказать о расположении прямых? (Они проведены через одну точку.)

– Сколько прямых можно провести через одну точку? (Сколько угодно.)

– Вы вспомнили о точке, самой маленькой жительнице геометрии. Отметьте в тетради две точки, и не забудьте о правиле, как надо ставить точку.

Учитель отмечает две точки на доске.

– Обозначьте эти точки латинскими буквами А и В. Какими должны быть эти буквы? (Заглавными.)

– Проведите через точки А и В прямую.

Учитель делает чертёж на доске, дети – в тетрадях. Принципиально важно, чтобы точки не ограничивали прямую.

– Как вы думаете, сколько прямых можно провести через две точки? (Только одну.)

– С этим как раз и связано обозначение прямой двумя большими буквами. Прочитайте название этой прямой. (АВ.)

– Как ещё можно обозначить прямую? (Одной маленькой латинской буквой, например, f.)

3) Разбиение пар прямых на группы. Задание для пробного действия.

Раздать карточки с заданием для пробного действия.

– Вы уже немало знаем о прямых. Посмотрите на карточку. На какие две группы можно разбить эти пары прямых по их расположению относительно друг друга? (На пересекающиеся и непересекающиеся прямые.)

Учитель прикрепляет на доску карточки: .

– Что вы повторили? (Точку, отрезок, прямую, её построение.)

– Какие варианты расположения прямых вы выделили? (Пересекающиеся и непересекающиеся.)

– Что дальше? (Вы дадите задание, в котором будет что-то новое.)

- С какой целью я вам такое задание? (…)

– Послушайте задание и определите, что в нём для вас нового. Вам надо выявить, на каких карточках пары прямых пересекаются, а на каких не пересекаются, и записать номера этих карточек в соответствующий столбик на маленьких строчках.

– Что в этом задании для вас нового? (Нам не приходилось определять, какие прямые пересекаются, а какие не пересекаются.)

– Что вы будете делать? (Попробуем определить, какие пары прямых пересекаются, а какие – нет.)

– Пробуйте.

– Проверим.

Учитель открывает на доске такой же чертёж, причём на нём должны быть обозначены границы маленьких карточек и граница листа.

– Назовите номера карточек, на которых, по вашему мнению, изображены пересекающиеся прямые. (…)

Учитель фиксирует на доске все варианты ответов детей.

– Назовите номера карточек с изображением непересекающихся прямых. (…)

Учитель фиксирует на доске все варианты ответов детей.

– Итак, признак разбиения у вас одинаковый, но что вы видите? (По-разному распределены пары прямых на эти две группы, т.е. мнения разделились.)

– Чего же вы не смогли сделать? (Мы не смогли определить, где пересекающиеся прямые, а где – непересекающиеся.) (Мы не можем доказать, верно ли распределены пары прямых на пересекающиеся и непересекающиеся.)

3. Выявление места и причины затруднения.

Цель:

организовать выявление и фиксацию учащимися места и причины затруднения.

Организация учебного процесса на этапе 3:

– Что необходимо сделать, если вы зафиксировали, что трудность есть? (Надо остановиться и подумать.)

– Назовите признак разбиения пар прямых, который вы выбрали. (Пересекающиеся и непересекающиеся прямые.)

– Какое задание вы выполняли? (Надо было выявить, какие прямые пересекаются, а какие не пересекаются, и записать номер карточки в нужный столбик.)

– Расскажите, как вы действовали (рассуждали), выполняя это задание? (…)

– Когда, на каком шаге ваших рассуждений была неуверенность в том, правы вы или нет? (…)

– Почему же мнения разделились? (Мы не знаем, как определить – пересекаются или не пересекаются прямые на некоторых карточках.)

4. Построение проекта выхода из затруднения.

Цель:

1) сформулировать цель учебной деятельности;

2) выбрать способ и средства для построения нового знания.

Организация учебного процесса на этапе 4:

– Поставьте перед собой цель. (Нам надо найти способ, по которому можно определить, пересекаются прямые или нет.)

– Значит, какова тема урока? (Пересекающиеся и непересекающиеся прямые.)

Открыть тему на доске.

– Какие знания и умения вам необходимы для построения нового способа? Вспомните, что я выбрала для повторения в начале урока. (Знание о том, что такое прямая, умение строить прямые.)

– Расскажите, как вы воспользуетесь этими знаниями и умениями для построения способа определения пересекающихся и непересекающихся прямых? (Вспомним и проговорим, что такое прямая; попробуем продолжить прямые, …)

– А в какую сторону вы будете продолжать прямые, вы сейчас можете сказать? (Пока не можем.)

– Итак, вы сначала повторите то, что вы знаете о прямой.

Постепенно отрывать на доске план действий или лучше записывать мелом на доске:

1. Что мы знаем о прямой.

– Потом? (Продолжим прямые.)

2. Продолжить прямые.

– Продолжая прямые, над каким вопросом вы задумаетесь? (В какую сторону продолжать?)

3. В какую сторону продолжать?

– Зачем вы будете продолжать прямые? (Чтобы понять, сможем ли мы таким образом выявить пересекающиеся прямые.)

4. Проверить предположение.

– И если окажется, что вы правильно построили план действий, то …? (Выведем общий способ.)

5. Способ.

5. Реализация построенного проекта.

Цель:

1) организовать построение детьми нового способа действий, устраняющего причину затруднения, с использованием представлений детей о прямой и о способе построения прямых с помощью линейки;

2) сформировать у учащихся на основе понимания нового способа представления о непересекающихся (параллельных) прямых;

3) применить новый способ для выполнения задания, вызвавшего затруднение;

4) зафиксировать новый способ действий в речи и в виде опорного сигнала;

5) зафиксировать преодоление возникшего затруднения.

Организация учебного процесса на этапе 5:

– Итак, действуем по плану. С чего начнём? (Повторим, что мы знаем о прямой.)

– Повторите. (Её можно продолжить в обе стороны, на ней можно отложить отрезки любой длины, …)

– Что для вас здесь важно? (То, что прямую можно продолжить в обе стороны.)

– Что вы запланировали делать дальше? (Продолжить прямые и понять, в какую сторону их надо продолжать.)

– Начнём с пятой карточки. Посмотрите на прямые и ответьте на свой вопрос: в какую сторону продолжать? (В сторону их сближения.)

– Продолжим прямые.

– Что видите? (Прямые пересеклись.)

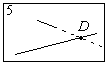– Отметим точку пересечения прямых и обозначим её, например, D.

Здесь и далее учитель выполняет те же действия на доске:

– К какой группе относятся прямые на пятой карточке? (К группе пересекающихся прямых.)

После нахождения и обозначения точки пересечения карточка помещается в соответствующую группу: пересекающихся (если точку пересечения не нашли – в группу непересекающихся).

– Что дальше по плану? (Проверить предположение.)

– Проверьте своё предположение, смогли вы определить, продолжая прямые в сторону сближения, пересекаются они или нет? (Смогли, предположение было верным.)

– Что осталось сделать, чтобы полностью реализовать план? (Вывести общий способ.)

– Итак, как определить, пересекаются ли прямые, если точки пересечения на чертеже нет? (Продолжить прямые в сторону сужения.)

– Молодцы! Давайте применим построенный вами способ для выяснения, на каких из оставшихся карточках прямые пересекаются, а на каких нет. Работаем с 4-ой карточкой. Как будете действовать? (Продолжим прямые.)

– Выполняйте.

– Что видите? (Прямые не пересекаются, и расстояние между ними не изменяется.)

– А если продолжить прямые за карточку? (Они всё равно не пересекутся.)

– Значит, к какой группе отнесём эту пару прямых? Почему? (К группе непересекающихся прямых, так как прямые не сближаются, нет точки пересечения.)

Переместить 4-ую карточку к группе непересекающихся.

– Проверьте, в какой группе записан у вас номер этой карточки. Если ошиблись – исправьте.

– Что можете сказать о прямых на 3-ей карточке? (Это пересекающиеся прямые, так как есть точка пересечения.)

– Проверьте, что номер 3 у вас стоит в группе пересекающихся прямых.

– Следующая карточка № 2. Что вы можете сказать о прямых на ней? (Они не сближаются, значит, они не пересекутся.)

– Проверим это, продолжив их в обе стороны.

Учитель выполняет те же действия на доске и перемещает 2-ую карточку к группе непересекающихся прямых.

– Обратимся к карточке № 1. Как вы считаете, прямые на этой карточке пересекающиеся или нет? (Пересекающиеся, так как расстояние между ними уменьшается; нет, так как …)

– Чтобы проверить ваши предположения, что предлагаете сделать? (Продолжить прямые.)

– В какую сторону продолжим прямые? (В сторону сужения.)

– Продолжим и найдём точку пересечения.

Учитель продолжает прямые до границы листа.

(Мы не можем найти точку пересечения, так как лист закончился.)

– Значит, эти прямые не пересекаются? (Пересекаются, так как расстояние между ними уменьшается.)

– Как же это доказать? (Продолжить прямые «за карточку» и найти их точку пересечения.)

Раздать чистые листы А–4. Учитель на доске, а учащиеся на листах продолжают прямые за границу «листа».

– Что вы можете сказать о взаимном расположении этих прямых? (Они пересекаются.) Отметьте точку пересечения.

Учитель помещает карточку № 1 в группу пересекающихся прямых.

– Итак, посмотрите ещё раз на все карточки, которые вы поместили в группу пересекающихся прямых. Какие прямые называют пересекающимися? (Те, которые имеют точку пересечения.)

– А как определить, пересекаются ли прямые, если точки пересечения на чертеже нет? (Продолжить прямые в сторону сужения.)

– А если нет такой возможности: нет карандаша и линейки или закончился лист? (Надо мысленно продолжить прямые.)

– Верно. Сколько точек пересечения может быть у пересекающихся прямых? Почему? (Только одна, так как прямые, пересекаясь, «расходятся».)

Повесить на доску опорный сигнал:

– Какие прямые не имеют точки пересечения? Почему? (Непересекающиеся, так как расстояние между ними не изменяется.)

– Непересекающиеся прямые называют параллельными.

Повесить на доску опорный сигнал:

– Итак, какие же варианты взаимного расположения прямых существуют? (Прямые могут пересекаться или быть параллельными.)

– Могут ли быть другие варианты взаимного расположения прямых? (Нет, так как у двух прямых не может быть больше одной общей точки. Значит, либо её нет, либо она одна.)

6. Первичное закрепление с проговариванием во внешней речи.

Цель:

создать условия для выполнения учащимися типовых заданий на использование нового способа действий с проговариванием во внешней речи.

Организация учебного процесса на этапе 6:

– Вы построили новый способ. Что дальше? (Надо потренироваться в его применении.)

1) Параллельные прямые.

Стр. 6-7.

– Откройте учебник на страницах 6 и 7. Посмотрите на разворот страниц и найдите параллельные прямые. (Прямые в № 4, стр. 7.)

– Почему вы считаете, что они параллельны? (Потому что они не пересекутся, сколько их не продолжай.)

2) Пересекающиеся прямые.

№ 3 (а), стр. 6 (задание выполняется в парах, поверка проводится фронтально).

Задание:

Проведи прямые EF и MK. Обозначь их точку пересечения буквой О.

. М . F

Е . . К

Решение:

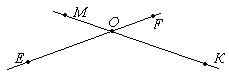
– А теперь выполним задание № 3 (а), стр. 6. Прочитайте задание.

– О каком отличительном признаке прямой нужно помнить, чтобы провести прямую через две точки? (У прямой нет ограничений на концах, значит, линию будем проводить дальше точек.)

– Выполним это задание.

Открыть на доске отмеченные точки, как в задании. Один ученик выполняет задание на доске, остальные – в тетради.

– Сколько точек пересечения прямых вы отметили? (Одну.)

– Как называются прямые MК и ЕF? (Пересекающиеся.)

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на нахождение точки пересечения прямых с самопроверкой по опорному сигналу;

2) организовать самооценку детьми правильности выполнения задания;

3) создать (по возможности) ситуацию успеха для каждого ребёнка.

Организация учебного процесса на этапе 7:

– Молодцы! Вы отлично справились с заданиями, связанными с темой урока. А теперь… (Самостоятельная работа.)

– Для чего вы выполняете самостоятельную работу? (Чтобы выяснить, какие остались трудности и для того, чтобы их преодолеть.)

–

Задание:

Найди точку пересечения прямых а и b на рисунке и обозначь её Т.

а b

Решение:

Выполните задание в учебнике: № 3 (б), стр. 6.

Для выполнения задания даётся 1 мин.

– Проверьте себя по образцу на доске.

Открыть на доске образец решения.

– Поднимите руки у кого возникли затруднения. В чём их причина? (Неправильно приложили линейку, не продолжили прямые линии, не в ту сторону продолжили, …)

– Как исправить ошибки? (Потренироваться пользоваться линейкой, понять, что такое прямая, …)

– Кому всё удалось? Отметьте свою работу знаком «+».

– Какой из вариантов взаимного расположения прямых у вас получился? (Пересекающиеся прямые.)

8. Включение в систему знаний и повторение.

Цель:

1) организовать повторение соотношения единиц измерения длины;

2) повторить решение задач на нахождение целого.

Организация учебного процесса на этапе 8:

1) Прямая и отрезок.

№ 5, стр. 7 (без обращения к учебнику).

– Продолжаем путешествие по Геометрии. Как-то лучшие друзья – отрезок и прямая – заспорили о том, что у них общего и чем они отличаются. За помощью они обратились к точке. Как вы думаете, что ответила точка отрезку и прямой? Чем они похожи и чем отличаются? (Отрезок и прямая похожи тем, что чертить их надо по линейке, отличаются тем, что отрезок имеет ограничения, прямая бесконечна; точка может перемещаться по прямой – сколько угодно в любую сторону, а по отрезку – только между его концами; длину отрезка можно измерить, а длину прямой – нет .)

2) Соотношение единиц измерения длины.

№ 6, стр. 7.

– Вы сказали, что длину отрезка можно измерить. Какие единицы измерения длины вы знаете? (Сантиметр, дециметр.)

– Выполним № 6 на стр. 7. Прочитайте задание.

Задание:

Вырази в новых единицах измерения:

50 см = …дм 3 дм 6 см = …см

78 см = …дм …см 9 дм = … см

Решение:

50 см = 5 дм 3 дм 6 см = 36 см

78 см = 7 дм 8 см 9 дм = 90 см

– Что, значит, выразить в новых единицах измерения? (Дециметры перевести в сантиметры и сантиметры перевести в дециметры.)

– Что надо помнить, чтобы перевести дециметры в сантиметры и наоборот? (Что 1 дм = 10 см.)

– Выполним задание. (10 см = 1 дм, значит, 50 см = 5 дм; …)

По одному с места с объяснением.

3) Решение задачи.

№ 8 (б), стр. 7.

– Вы заканчиваете путешествие по стране Геометрии, и почему бы вам по дороге не решить задачу?

– Прочитайте условие задачи № 8 (б) на стр. 7.

– Выполните анализ задачи.

По одному с места. Один ученик продолжает ответ другого.

В случае затруднений у учащихся в ходе анализа учитель задаёт опорные вопросы (см. ниже).

– Что известно в задаче? (С одной яблони собрали 21 кг яблок, что на 14 кг меньше, чем со второй.)

– Что надо узнать в задаче? (Сколько килограммов яблок собрали с двух яблонь.)

– Начертите и заполните схему к задаче.

Один у доски, остальные – в тетрадях.

– Что надо сделать, чтобы ответить на вопрос задачи? (Надо сложить массу яблок, собранную с каждой яблони, т.к. ищем целое.)

– Можете сразу ответить на вопрос задачи? (Нет, т.к. не знаем, сколько килограммов яблок собрали со второй яблони.)

– Можем ли вы это узнать? Как? (Можем. Нам известно, что с первой яблони собрали на 14 килограммов меньше, чем со второй. Значит, со второй яблони собрали на 14 килограммов больше. Поэтому, чтобы найти массу яблок, собранных со второй яблони надо сложить, т.к. ищем большее число.)

– Расскажите план решения задачи. (Первым действием мы узнаем, сколько килограммов яблок собрали со второй яблони. Вторым действием мы ответим на вопрос задачи.)

– Запишите решение.

Один у доски, остальные – в тетради. После завершения записи решения несколькими учениками, учитель напоминает учащимся, как провести самостоятельный анализ задачи, сам показывая им образец правильного ответа.

9. Рефлексия учебной деятельности на уроке.

Цель:

1) организовать самооценку учащимися своей учебной деятельности на уроке;

2) зафиксировать степень соответствия цели и результата учебной деятельности;

3) зафиксировать в речи изученные на уроке понятия пересекающихся и непересекающихся прямых и способ их нахождения;

4) зафиксировать затруднения, которые остались, и способы их преодоления;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

– Итак, какие варианты взаимного расположения прямых вы знаете? (Прямые могут пересекаться, могут быть параллельными.)

– Какова была цель сегодняшнего урока? (Выяснить способ определения пересекающихся и непересекающихся прямых.)

– Достигли ли вы цели? Докажите. (…)

– Как определить, пересекаются прямые или нет, если на чертеже нет точки пересечения? (Надо мысленно продолжить прямые в сторону сужения.)

– Какие трудности встретились? Удалось ли их преодолеть? Как?

– Над чем надо поработать?

– Как вы оцениваете свою работу на уроке?

– На сегодня вы завершаете путешествие с точкой и прямой.