Конспект урока «Угол между прямой и плоскостью. Решение задач» по математике

Тема: Угол между прямой и плоскостью. Решение задач.

Тип урока: урок применения и закрепления знаний.

Цели урока:

• повторить понятия перпендикуляр, наклонная и ее проекция и основные теоремы курса планиметрии, отражающие соотношения в прямоугольном треугольнике;

• продолжить формирование умений находить угол между прямой и плоскостью;

• продолжить формирование умений обосновывать или опровергать выдвигаемые предположения;

• развивать пространственное мышление, самостоятельность и умение преодолевать трудности в учении;

• воспитывать   интерес к предмету.

Оборудование: ПК, проектор, презентации к уроку, учебники геометрии, таблица Брадиса, таблица значений тригонометрических функций некоторых углов, чертежные инструменты, микрокалькулятор.

Ход занятия:

1. Организационный момент.

2. Актуализация знаний. Тема нашего сегодняшнего занятия «Угол между прямой и плоскостью. Решение задач». В течение занятия мы повторим понятие угла между прямой и плоскостью и рассмотрим, как данная тема применяется при решении геометрических задач, а также при решении, так называемых, задач практического содержания. А начнем мы с повторения тех сведений, которые могут нам при этом пригодиться.

Устные упражнения:

Задача 1. В треугольнике АВС катеты равны 16 и 12 см. Найдите длину гипотенузы.

Решение: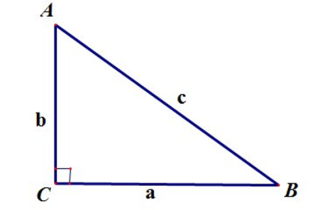

;

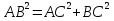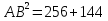
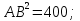
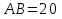см.

Задача 2. В треугольнике АВС длина ВС рана 2 см, а длина гипотенузы АВ – 4 см. Определите градусные меры углов В и А.

Решение: Так как гипотенуза в два раза длиннее катета, то угол А равен 30 градусов, а угол В 60 градусов.

Задача 3. Длина катета b треугольника АВС равна 6, а катета а - 6√ см. Вычислите тангенс угла А.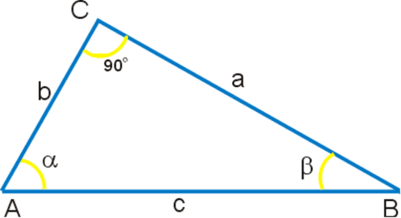

Решение: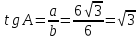

Задача 4. Медианна правильного треугольника АВС равна 33 см. Найдите длину отрезка АО. Чем является этот отрезок для треугольника АВС?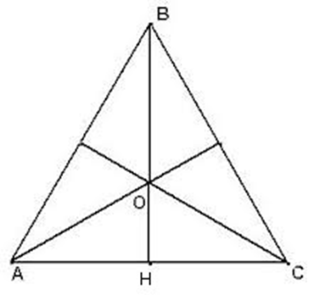

Отрезок АО является радиусом описанной окружности.

Длина этого отрезка равна

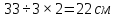. ой и плоскостью.

Вопрос 1. Как можно вычислить радиус окружности, описанной около правильного треугольника? Предложите несколько способов нахождения. Ответ: 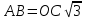. В формулах АВ длина стороны треугольника, ОС – радиус.

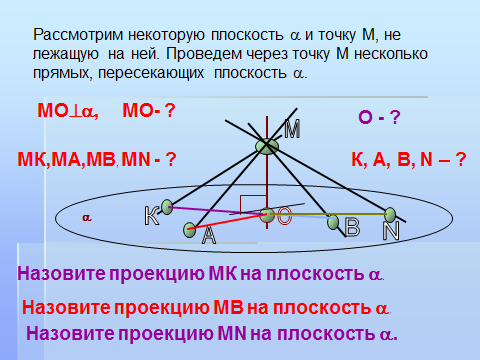
Для дальнейшей работы повторим основные понятия, которые необходимы для определения угла между прямой и плоскостью.

Задача 5. Из точки А к плоскости проведен перпендикуляр АН и наклонная АМ длиной 17 см. Длина ее проекции МН на эту плоскость 8 см. Вычислите синус и косинус угла между наклонной и ее проекцией.

Решение: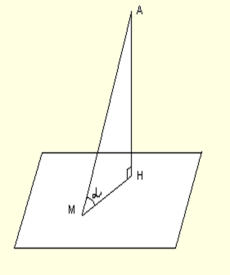

По теореме Пифагора длина перпендикуляра 15 см. Косинус угла.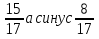

Тригонометрические функции острого угла прямоугольного треугольника – это один из основных методов решения задач. Кому же впервые пришло в голову использовать соотношение между сторонами и углами прямоугольного треугольника? Об этом нам расскажет _______.

Один из студентов представляет доклад с презентацией о возникновении тригонометрии.

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников. Возникновение тригонометрии связано с землемерием, астрономией и строительным делом. С помощью тригонометрических функций острого угла прямоугольного треугольника можно вычислить ширину реки, высоту дерева. С их помощью были составлены таблицы, по которым вычисляются расстояния между космическими объектами, длины трасс авиа портов.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями. С 17 века тригонометрические функции стали глубоко исследоваться и сыграли важную роль в математике. Своим становлением тригонометрия обязана арабским учёным Аль-Батани, Абу-ль-Вафа, Мухамед-бен Мухамед, индийскому учёному Бхаскара и азербайджанскому астроному и математику Насиреддин Туси Мухамед, который в своих трудах обозначил тригонометрию как самостоятельную дисциплину.

И только в 18 веке знаменитый математик, член Петербургской Академии наук Леонард Эйлер провел блестящий математический анализ и первым ввел известные всем определения тригонометрических функций. С именем этого ученого связано возникновение тригонометрических формул, которые в свою очередь позволили сделать более лаконичными и простыми доказательства различных фактов. Математика продвинулась на большой шаг вперёд. Новые формулы значительно облегчили исследования в области механики, оптики, электричества, радиотехники, астрономии и т. п.

Запись тригонометрических формул происходит с использованием понятий: синус, косинус, тангенс, котангенс, которые также имеют свою историю возникновения.

Синус (изгиб) встречался в трудах по астрономии великого индийского учёного Ариабхаты и имел название - архаджива, затем слово было сокращено на джива, и лишь в 19 веке слово было заменено арабами на джаб, перевод которого и означал современный термин.

Косинус (дополнительный синус) очень молод по сравнению с другими, так как появился совсем недавно.

Тангенс и котангенс возникли ещё в 10 веке, благодаря арабскому математику Абу-ль-Вафойно. Но понятие было забыто и заново открыто лишь в XIV веке немецким математиком, астрономом Регимонтаном.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греческого gwnia - угол, metrew- измеряю). Термин гониометрия в последнее время практически не употребляется.

Итак повторим как определяется угол между прямой и плоскостью.

Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называют угол между прямой и её проекцией на плоскость .

При решении задач углом между прямой и плоскостью будет служить угол между наклонной и её проекцией. Наибольшее затруднение при построении такого угла вызывает построение перпендикуляра от точки до плоскости. Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.

Задача 6. В кубе A…D₁ найдите угол между прямой AA₁ и плоскостью ABC.

Решение: Ребро АА₁ перпендикулярно плоскости АВС, поэтому искомый угол равен 90 градусов.

Задача 7. В кубе A…D₁ найдите угол между прямой AB₁ и плоскостью BCC₁.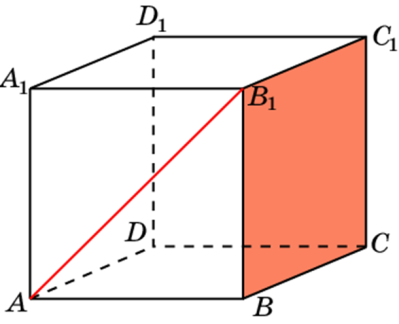

Из равнобедренного треугольника АВВ₁ угол АВ₁В равен 45 градусов.

Задача 8. № 163. Задача решается по вариантам: 1-а, 2-б, 3-в. Решение комментируется представителем студента решавшего задание варианта.

Задача 9. Каждое боковое ребро тетраэдра равно 4 см и образует с плоскостью основания угол равный 30 градусам. Вычислите расстояние от вершины А тетраэдра до плоскости основания и длину ребра его основания.

Решение: Опустим из вершины тетраэдра А на плоскость ВСД перпендикуляр АН. Треугольники АВН, АСН, АДН равны по гипотенузе и острому углу, следовательно ВН=СН=ДН=R. АН=2(свойство прямоугольного треугольника), по теореме Пифагора ВН=2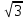

R=2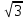 ВС=2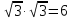

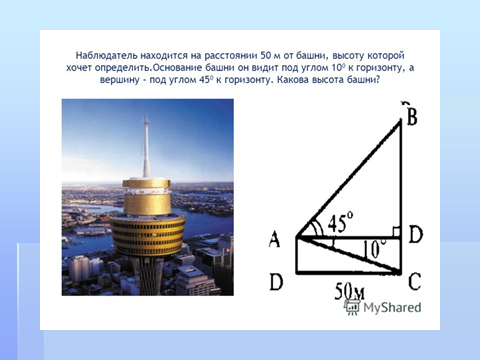
Понятие угла между прямой и плоскостью довольно часто приходится использовать при решении задач практического содержания. На слайдах вы можете видеть некоторые из них. Предлагаю вам решить по одной задаче, объединившись для работы в группы. Решение задач старший группы представит для проверки вместе с оценкой степени вложения каждого представителя группы при решении задачи.

Подведем итог занятия. Какие основные понятия были повторены в течении урока? Ответы студентов.

Задание на дом: Раздать распечатки с заданиями для домашней работы.