Конспект урока «Системы мер» по математике для 5 класса


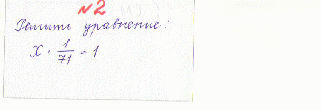
 Занятие в математическом кружке по теме «Системы мер» для 5-6 классов
Занятие в математическом кружке по теме «Системы мер» для 5-6 классов
Цель: Расширить знания учащихся о старинных русских мерах.
Выявить наиболее распространенные старинные меры, которые использовались и используем в жизни.
Задачи:
Познакомиться с измерительной системой, которая существовала ранее.
Установить взаимосвязь между старой измерительной системой и новой.
Это занятие мы проведём в форме МАТЕМАТИЧЕСКОЙ ИГРЫ «ХОЧУ ВСЁ ЗНАТЬ»
«ЧЕЛОВЕК – МЕРА ВСЕХ ВЕЩЕЙ».
С незапамятных времён человеку приходилось измерять расстояния в связи с изготовлением простейших орудий труда, со строительством жилищ и добавлением пищи. Подобно тому как при счёте человек пользовался вначале пальцами рук и ног, так и при измерении расстояний он прибегал к рукам и ногам. Вот почему в прошлом мерами длины служили ( да иногда и теперь ещё служат) ШАГ, ЛАДОНЬ – ширина кисти руки, и сейчас мы с вами узнаем что ещё?
ЗАДАНИЕ: это задание выполнять по рядам (всего 6 вариантов). Вычисли значение выражения 0,2* Х – 0,2
| №2 | №3 | №4 | №5 | №6 | |
| 0,6 | 0,1 | 0,2 | 0,1 | 0,4 | 0,8 |
| Л | О | К | О | Т | Ь |
ОТВЕТ: ЛОКОТЬ.
Локоть – это расстояние от локтя до конца среднего пальца.
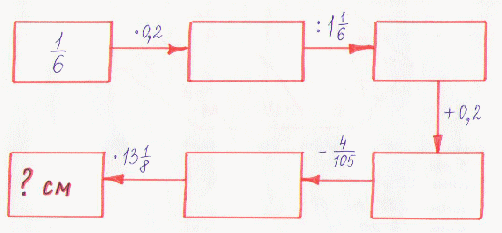
Названия мер у разных народов свидетельствуют об их происхождении от различных частей человеческого тела. Например, слово «ДЮЙМ» (английская, а также старая русская мера длины означает на голландском языке «большой палец». Сейчас мы узнаем, сколько см составляет 1 дюйм.
ЗАДАНИЕ:
Итак, в 1 дюйме приблизительно 2,5 см.
Слово «ФУТ» (старая мера длины) означает на английском языке «нога». Эта мера длины возникла как средняя длина ступни человека. Отсюда и известный афоризм: «Человек – мера всех вещей».
ЗАДАНИЕ: Найти 25% от 122
Итак, в 1 футе приблизительно 30,5 см.
С развитием производства и торговли люди убедились в том, что не всегда удобно измерять расстояния шагами или прикладыванием локтя. Кроме того, такое измерение уже не удовлетворяло возросшим требованиям точности. В самом деле, длина локтя или шага у разных людей различна, а мера длины должна быть const (Постоянные образцы мер стали изготовлять из деревянных линеек и металлических стержней. Образцы мер в настоящее время называются эталонами).
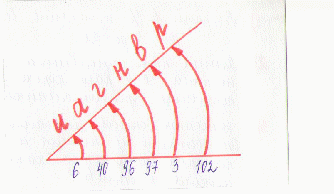
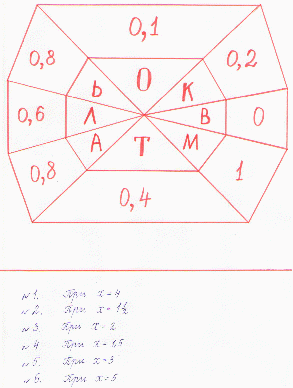
Узнаем, что является старой русской мерой длины. Это слово вы знаете. Давайте вместе вспомним.
ЗАДАНИЕ:
Используя математические часы, расшифруйте слово:
ОТВЕТ: АРШИН
ВОПРОС. Сколько см в 1 аршине?
ЗАДАНИЕ:
ОТВЕТ: 71 см
Итак, в 1 аршине 71 см. выразите 71 см в м, дм, мм.
Аршин делился на какое-то количество вершков. А именно на 16. Сколько см в 1 вершке?
(71 : 16 = 4,4375 см ). Округлите ответ до десятых.
Значит, в 1 вершке приблизительно 4,4 см.
ЗАДАЧА. Найди число, 75% которого составляют 12.
А если взять 3 аршина, то это уже будет (ЧТО?)
ЗАДАНИЕ: поменять карточки с одинаковыми ответами местами, и у вас получится нужное слово
ОТВЕТ: САЖЕНЬ
Для измерения площадей применялись квадратные сажень, аршин, фут, дюйм, вершок. Основной земельной мерой, начиная с 16 века, служила десятина, равная 2400 кв.саженей. Вычислим 1 десятину в га.
ЗАДАНИЕ: наименьшее из полученных значений подскажет вам ответ на вопрос.
-
Найти 0,2 от 5,5
-
Найти 75% от 2,4
-
Найти 0,7 от 5
-
Найти 0,24 от 10
-
Найти 15% от 8
Ответ: 1,1.
Значит, в 1 десятине – 1,1 га.
В древности мера веса часто совпадала с мерой стоимости товара, т.е. с денежной единицей. Это объясняется тем, что деньги выражались в весе серебра или золота.
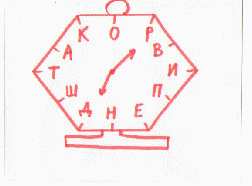
Вопрос. В Древней Руси что служило одновременно и основной весовой единицей, и денежной единицей? Мы сейчас узнаем.
ЗАДАНИЕ:
ОТВЕТ: ГРИВНА.
Гривна – это слиток серебра, вес которого был приблизительно равен фунту, содержащему 96 золотников.
Задание: 409512 : 1000 =
Этот ответ позволяет нам узнать, сколько граммов содержится в 96 зол.
ОТВЕТ: 409,512 г.
Во второй половине XIII века гривну стали рубить пополам, и новый слиток в половину денежной гривны, названный РУБЛЁМ, стал в XV веке основной денежной единицей.
Вопрос. Почему копейку называют копейка?
ИЗВЕСТНО, ЧТО:
1 см = 0,394 дюйма
Сколько сантиметров содержится в дюйме?
В 1 дюйме содержится приблизительно 2,54 см
1 бочка = 40 вёдер = 491,96 л
Сколько литров в 1 ведре?
В 1 ведре приблизительно 12, 299 л
1 аршин = 16 вершков = 0,7112 м
Сколько метров в 1 вершке?
В 1 вершке - 0,04445 м
1 верста = 500 саженей = 1, 0668 км
Сколько км составляет 1 сажень?
В 1 сажени приблизительно 0,00213 км
ВЫВОД:
1 ДЮЙМ = 2,5 см
1 ФУТ = 30,5 см
1 АРШИН = 71 см
1 ДЕСЯТИНА = 1,1 га
1 ГРИВНА = 409,512 г
Запомним это.
Источники материалов:
http://nsportal.ru/shkola/algebra/library/2013/06/23/matematika
Здесь представлен конспект к уроку на тему «Системы мер», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (5 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

