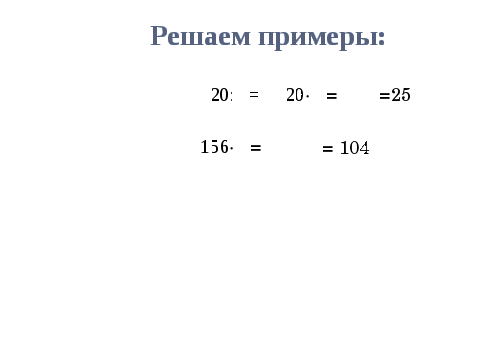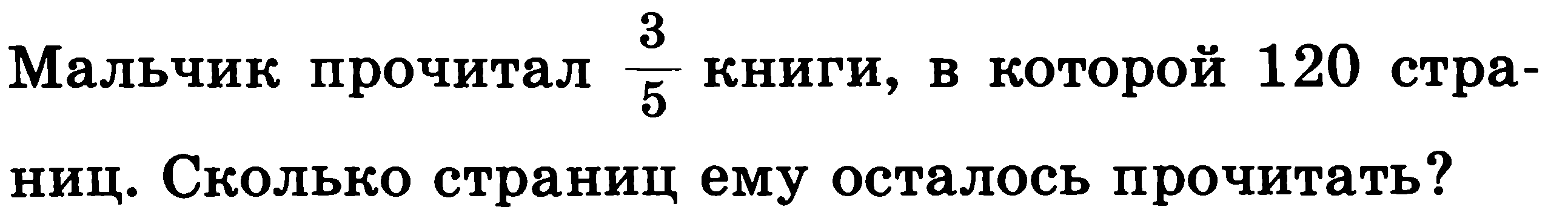Конспект урока «Нахождение части от целого и целого по его части» по математике для 5 класса

Тема урока

Нахождение части от целого и целого по его части.

Предмет

математика

Класс

5

Автор урока

Демидова Татьяна Анатольевна

Образовательное учреждение

МАОУ «СОШ № 132», г.Барнаул

Методическая информация

Тип урока

Урок формирования новых знаний по теме «Нахождение части от целого и целого по его части»

Цели урока

Научиться определять тип задачи на нахождение части от целого и целого по его части;

Способствовать развитию логического мышления, умения анализировать;

Формировать навыки оформления записей, самостоятельность мышления и интерес к изучению предмета.

Задачи урока

Образовательные:

продолжить формирование понятия обыкновенной дроби, познакомить учащихся с понятиями: целое, часть от целого, сформулировать правила нахождения части от целого и целого по его части, показать применение этих правил при решении задач;

Развивающие: развивать логическое мышление, умение анализировать, продолжить работу по развитию математической речи;

Воспитательные: формировать эстетические навыки при оформлении записей, развивать навыки самоконтроля, на примере задач показать практическую значимость данной темы, формировать у учащихся самостоятельность мышления и интерес к изучению предмета.

Здоровьесберегающие:

профилактика умственного перенапряжения путем смены видов деятельности, физкультминутки.

Формы и методы

Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока

Беседа, фронтальный опрос, индивидуальная работа с дидактическим материалом, отработка терминов, индивидуальная работа у доски, решение проблемных задач.

Понятия: дробь как одна или несколько равных долей; элементы дроби.

Навыки и умения решать задачи на нахождение части от целого и целого по его части.

Необходимое оборудование и материалы

Компьютер, проектор, экран, тетради, учебник, раздаточный материал, распечатанный на принтере.

Подробный конспект урока

Мотивация учащихся

Введение нового материала с помощью учебно-познавательных заданий, их выполнение дает учащимся возможность самостоятельно или с минимальной помощью учителя открыть новое для себя теоретическое знание, т.е. совершить субъективное открытие.

Ход и содержание урока

Тема: “ Нахождение части от целого и целого по его части ”

Ход урока

1. Организационный момент

Цель - вспомнить изученный материал, обобщить, подготовить учащихся к восприятию новой темы.

Здравствуйте, ребята. Садитесь.

Для того чтобы нам с вами сегодня плодотворно поработать на уроке необходимо сформулировать тему урока и поставить перед собой цель урока. Было бы очень хорошо если бы вы это сделали сами. Что бы вы смогли это сделать , нам нужно выполнить подготовительную работу. Итак первое задание .

2. Актуализация знаний (устный счёт)

Слайд 1

Продолжите предложение:

1. « Двухэтажная» запись называется… обыкновенной дробью.

2 - это числитель дроби,

3 - это знаменатель дроби

2. Знаменатель дроби показывает…

…на сколько равных частей разделили целую величину. Числитель дроби показывает…

…сколько таких частей взяли.

Следующее задание.

Слайд 2

Определите, какая часть фигуры закрашена синим цветом:

Слайд 3

Разделите задачи на две группы:

1. Магазин принял для продажи 156 кг рыбы. всей рыбы составил карп. Сколько кг карпа получил магазин?

2. Провели 18 опытов, это составило всей серии опытов. Сколько опытов надо провести?

3. Учитель проверил 20 тетрадей. Это составило всех тетрадей. Сколько всего тетрадей надо проверить?

4. Из 72 пятиклассников занимаются легкой атлетикой. Сколько учащихся занимаются этим видом спорта?

5. Для выставки отобрали 30 картин, что составило имеющихся в музее картин. Сколько картин взято на выставку?

6. От веревки 18 м отрезали ее длины. Сколько метров веревки отрезали?

(Задачи читают ученики вслух по очереди.)

-Минутку подумайте и назовите номера задач , которые вы отнесете к 1-ой группе.

Слайд 4.

-Назовите номера задач, которые вы отнесете ко второй группе.

-Каким принципом руководствовались, осуществляя деление задач на группы?

-Как мы можем озаглавить первую группу задач?( Задачи на нахождение части целого .)

-Как мы озаглавим вторую группу задач? (Задачи на нахождение целого по его части.)

Откройте тетради, запишите число , классная работа.

Итак какая же тема нашего урока сегодня? Записываем ее в тетрадь..

Слайд 5.

Тема: “ Нахождение части от целого и целого по его части ”.

- Значит, чему мы будем учиться сегодня на уроке?

Научимся анализировать условие различных задач и относить их к тому или иному типу. А также рассмотрим разные способы решения таких задачи.

Предлагаю начать нашу работу с решения первых задач в каждой группе.

-Какая величина в задаче принята за целую?

-Известна ли она?

-Так как в задачи идет речь о третьих долях этой целой величины, строя схему отрезком какой длины нам удобно изобразить массу всей привезенной рыбы?

Слайд 6.

3. Объяснение новой темы на примере решения задач .

-Решая эти задачи с помощью рассуждений мы опирались на смысл дроби. Однако каждую из этих задач можно решить и другим способом. А каким давайте подумаем.

-Может кто-то уже готов предложить другой способ решения этих задач?

Для того чтобы задать направление ,в котором вам нужно двигаться в своих рассуждениях я предлагаю решить два примера.

Слайд 7.

4. Решаем примеры.

Учащиеся записывают решение в тетрадях ( далее следует самопроверка).

-Связаны ли эти примеры как то с теми задачами, которые мы решали только что?

(Связаны. Компоненты каждого действия это численные значения величин о которых идет речь в задачах которые мы решали)

- Какой способ решения задачи на нахождения части от целой величины можно использовать?

Чтобы найти часть от целой величины, выраженную дробью, нужно эту величину умножить на данную дробь.

- Какой способ решения задачи на нахождение целой величины по ее части можно использовать?

Чтобы найти целую величину по ее части , выраженной дробью, нужно разделить на эту дробь число, ей соответствующее.

Слайд 8. Правила.

5. Физкультминутка.

Правильный ответ поднимите руки вверх , неправильный – руки в стороны.

На доске снова появляется слайд с правилами.

6. Закрепление изученного материала, решение задач.

Ученики решают задачи у доски поочерёдно. Их работа оценивается.

Решаем задачи №888(а, б), 883 (а), 890(б). /// №887(а), 893(а).

7. Самостоятельная работа. (10 мин).

Вариант 1.

1.

2.

3.

Вариант 2.

1.

2.

3.

8. Рефлексия деятельности на уроке

Организация рефлексивной деятельности учащихся – самый трудный этап, задачи которого можно решить посредством беседы:

Итак, ребята, пришло время подводим итог урока.

Вы наверное заметили, что на протяжении всего урока мы решали задачи, которые встречаются в нашей повседневной жизни. Значит, умения решать задачи на нахождение части от целого и целого по его части пригодятся нам в жизни. 

Представьте, что урок уже закончился Вы идете домой после школы и встречаете своего друга или подругу.

• Что бы вы рассказали ему о урок математики, который у вас сегодня был?

• Что понравилось на уроке?

• Что бы вы хотели изменить в нашей работе?

9. Домашнее задание.

П. 9.6. учить правила № 889 (а), 890(а), 898(а).

Проверка и оценивание

В ходе урока учащиеся выполнили самостоятельную работу, за него получат оценки и отметку. Работа наиболее активных учеников также оценивается

В помощь учителю

Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить

Наглядность.

Слайды презентации с терминами, вопросами, позволяют существенно сэкономить время на уроке.

Использование ИКТ стимулирует познавательный интерес к предмету.

Советы по логическому переходу от данного урока к последующим

Данный урок позволяет закрепить понятие обыкновенная дробь, научиться отличать задачи на нахождение части от целого и целого по его части, а также выработает умение решать задачи на данные темы, что способствует грамотно перейти к изучению темы «Основное свойство дроби».