Конспект урока «Перпендикуляр и наклонная к прямой» по геометрии

Автор: Добриян Валентина Васильевна

Название ОУ: Лингвистическая школа- лицей

Должность автора: учитель математики

ТЕМА: Перпендикуляр и наклонная к прямой.

Цели:

а) образовательные – сформировать знания, умения и навыки построения перпендикуляра и наклонной к прямой;

б) развивающие – вырабатывать внимание, логическое мышление, грамотную речь, интерес к предмету;

в) воспитательные – прививать аккуратность, ответственность и уважение к одноклассникам, умение слушать, отстаивать свое мнение.

Основные термины и понятия: наклонная, проекция, среднее пропорциональное между

отрезками.

Планируемые результаты обучения: уч-ся должны знать основные понятия, уметь их

применять при решении задач.

Тип урока: изучение и первичное запоминание новых знаний и способов деятельности

Класс: 8

Ход урока

I. Организационный этап.

II. Актуализация знаний.

1. Что называют треугольником?

2. Соотношение между сторонами и углами треугольника.

III. Формирование новых понятий и способов действия

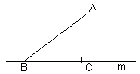
Рис. 1.

1) Рассмотрим прямую m и точку Аm (см. рис. 1 на доске и в тетрадях). Проведем [AC]m, Cm. Как называются: [AC]? Точка С? [перпендикуляр к прямой m; основание перпендикуляра] Сколько перпендикуляров можно провести из данной точки к данной прямой? Вm и В  С, [AB] – наклонная к прямой m;

В – основание наклонной;

[BC] – проекция этой наклонной, то есть, отрезок, соединяющий основания перпендикуляра и наклонной.

Сколько наклонных можно провести из точки А к данной прямой? Сравните длину любой и наклонной с длиной перпендикуляра.

Сформулируйте соответствующее свойство наклонной и докажите его. [Если из одной точки к прямой проведены перпендикуляр и наклонная, то длина наклонной больше длины перпендикуляра]

Теорема. Наклонные, проведенные из данной точки к данной прямой равны т. и т. т., когда равны их проекции.

Дано: Аm; [AC]m, Cm. [AB] и [AD] – наклонные к m.

Доказать: |АВ| = |AD|  |CВ| = |CD|.

Доказательство. 1) Если |АВ| = |AD|, то [AC] – высота в р/б ВАD, проведенная к основанию, следовательно, [AC] – медиана, то есть, |CВ| = |CD|, ч. т. д.

2) Если |СВ| = |CD|, то [AC] – высота и медиана в ВАD, значит он – р/б, то есть, |АВ| = |АD|, ч. т. д.

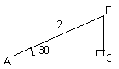
Решить задачи:

1) Найдите |АС| (см. рис. ) []

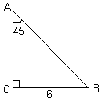
2) Найдите радиус окружности, описанной около треугольника АВС (см. рис. ) []

3) Между двумя фабричными зданиями устроен покатый желоб для передачи материалов. Расстояние между зданиями равно 10м, а концы желоба расположены на высоте 8м и 4 м над землей. Найдите длину желоба.

4) Из точки, не лежащей на данной прямой, проведен перпендикуляр к прямой, длина которого 24 см, и наклонная длиной 25 см. Найдите периметр образовавшегося треугольника.

5) Из точки, не лежащей на данной прямой, проведены к прямой две наклонные к₁ и к₂, проекции которых равны 5 см и 8 см соответственно. Какая из наклонных имеет большую длину? Ответ объясните.

Решение:

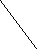
№5

5см 3см

V. Домашнее задание :

№ 1. Из точки, не лежащей на данной прямой, проведены перпендикуляр к прямой и наклонная длиной 26 см. Проекция наклонной на данную прямую равна 10 см. Найдите периметр образовавшегося треугольника.

№ 2. Из точки, не лежащей на данной прямой, проведены к прямой две наклонные к₁ и к₂, длина которых равны 14 см и 13 см соответственно. Какая из наклонных имеет большую проекцию? Ответ объясните.

VI. Подведение итогов урока : выставление оценок, выявление лучшего, поощрение отдельных учащихся и т. п.