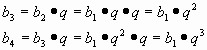Конспект урока «Сумма n первых членов геометрической прогрессии»
"Сумма n первых членов геометрической прогрессии"
Тип урока: изучение нового материала.
Технология обучения: проблемное.
Формы организации учебной деятельности: индивидуальная, фронтальная, коллективная.
Цели:
- продолжить формирование умения определять геометрическую прогрессию, знаменатель и n-ый член геометрической прогрессии;
- познакомить учащихся с формулой для нахождения суммы n- первых членов геометрической прогрессии;
- подготовка учащихся к итоговой аттестации;
- продолжить работу над развитием символического языка математики;
- развитие познавательного интереса учащихся;
- формирование понимания, что математический аппарат позволяет решать задачи из практической деятельности человека.
Ход урока
-
Организационный момент.
-
Постановка целей урока.
-
Повторение и актуализация опорных знаний.
-
Ознакомление с новым материалом.
-
Первичное осмысление и закрепление материала.
-
Задание на дом.
-
Поведение итогов.
2. Постановка целей.
Что изучали на предыдущем уроке?
Что будем делать сегодня на уроке?
3. Повторение и актуализация знаний учащихся.
КАРТОЧКИ 3 человека 3-5 мин
С остальными
Теор. опрос /слайд/ –
Какую прогрессию называют г.п? Что называют знаменателем г.п?
Какая прогрессия явл г.п.: А) 1, 8, 15,22,….
Б) 4;2;1;0,5….
В) 3,3,3,3…
Г) -2,4,-8,16…
Д) 4,7,10,13….
Е) 2,4,8,10….
Чему будем = знаменатель г.п.? Найдите ее пятый член?
По презентации задание ГИА
Какая из последовательностей является геометрической прогрессией?
А. Последовательность натуральных чисел кратных 3.
Б. Последовательность кубов натуральных чисел.
В. Последовательность натуральных степеней числа 3.
Г. Последовательность чисел, обратных натуральным.
В каких областях можно встретится с г.п. Вот, например, в биологии
Устно: В благоприятных условиях бактерии размножаются так,
что на протяжении одной минуты одна из них делится на две.
а) Сколько бактерий рождено на 3-й минуте от одной исходной?
б) Какова колония, рожденная одной бактерией за 3 минуты?
Пример из физики, экономико
4) ИНМ
Проблемная ситуация: Кому выгодна сделка?
Приходит как-то раз к одному богатому
купцу мужик и предлагает сделку.
«Давай, говорит, в течение месяца я
буду приносить тебе каждое утро по
100000 руб, а ты мне взамен в первый
день отдашь 1 коп, а в каждый последую-
щий в 2 раза больше. Во второй день-
2 коп, в третий- 4 коп и т.д.» Подумал купец и подписал договор.
Давайте проведем исследование этой проблемы и наметим пути решения
По презентации: Последовательность чисел 1; 2; 4; 8; 16;…
представляет собой геометрическую прогрессию,
у которой b1=1, q=2.
Следовательно, необходимо найти сумму первых
30 членов данной геометрической прогрессии. Каким образом??? Проблемная ситуация: Существует ли рациональный способ решения?
Существует еще одна древняя легенда о шахматах /рассказывает учитель вместе с детьми по ролям/
Ребята, в книге книге Перельмана Я. И. «Живая математика», есть легенда о шахматах: «…Шахматная игра была придумана в Индии, и, когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
- Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, - сказал царь…
- Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
- Простое пшеничное зерно? – изумился царь.
- Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…
- Довольно, - с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения доброты своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся. Покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унёс ли уже безрассудный Сета свою жалкую награду.
- Повелитель, - был ответ, - приказание твоё исполняется. Придворные математики исчисляют число следуемых зерен…
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.
Царь приказал ввести его.
- Прежде чем скажешь о твоем деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
- Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старик. – Мы добросовестно исчислили всё количество зерен, которое желает получить Сета. Число это так велико…
- Как бы велико оно ни было, - надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…
- Не в твоей власти, повелитель, исполнять подобные желания… »
Учитель: «Как мы узнали из этой легенды, о геометрической прогрессии знали ещё в древние времена. А почему царь не смог наградить изобретателя, как вы думаете? ».
Продолжим изучение нового материала.
Для того, чтобы узнать сколько Шераму пришлось бы отдать зерна, выведем с вашей помощью, аналогично арифметической прогрессии, формулу п – го члена геометрической прогрессии. Для этого рассмотрим один из ваших примеров
2; 6; 18, 54;
|
| |
| 18=6 |
|
| - - - - - - - - - - - - - - - - - - - | - - - - - - - - - - - - - - - - - - - - - - |
|
|
|
Итого получили формулу n-го члена геометрической прогрессии
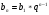
Давайте вернемся к задаче:
Сколько членов последовательности получилось?
Подставим в формулу:
5. Закрепление нового материала.
Сумма n первых членов геометрической прогрессии:
-
Sn=
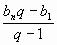 , q>1;
, q>1; -
Sn=
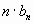 , q=1;
, q=1; -
Sn=
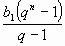 , 0
, 0
(Вывод формулы.)презентация
5а - Первичное осмысление и закрепление.
Из учебника №665 а,д, 667 а, 669 а
Проверь себя – презентация с-р /10 мин/ 1 вариант
1 вариант Обязательная часть.
Дана геометрическая прогрессия
-
b1=-4, q=2. Найти S5
-
b1=4, b2=16. Найти S6
Дополнительная часть.
3) Упростите выражение, применив формулу суммы n первых членов геометрической прогрессии:
1+х+х2+х3+х4=
х≠1
2 вариант
Обязательная часть.
Дана геометрическая прогрессия
-
b1=-9, q=2. Найти S6
-
b1=3, b2=9. Найти S5
Дополнительная часть.
3) Упростите выражение, применив формулу суммы n первых членов геометрической
прогрессии:
1+х+х2+х3+х4 +х5=
х≠1
6. Задание на дом П. 7.2 , формулы
№ 665(б, в), № 666
Найти (придумать) задачи на использование геометрической прогрессии из практической деятельности человека.
Примеры , которые нашел учитель.
-
В жилом микрорайоне открылся новый салон красоты, который в первый день посетило всего три клиентки. Каждая из них рассказала о салоне трем своим приятельницам, и те на другой день тоже посетили салон. В свою очередь, каждая из них рассказала о салоне трем своим знакомым, и те пришли на третий день. Если бы такая тенденция сохранилась в течении недели, то сколько человек посетило бы салон за неделю?
-
Некто приехал на пять дней в столицу и в первый день потратил на покупки некоторую сумму денег. В каждый следующий день он тратил денег в два раза больше, чем в предыдущий. Всего он истратил 15500 р. Сколько денег он истратил в первый день?
7. Подведение итогов. Рефлексия
Здесь представлен конспект к уроку на тему «Сумма n первых членов геометрической прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.