Слайд 1Лекция 2. Предел функции.
Понятие числовой функции Способы задания функции Характеристики функций Основные элементарные функции Предел функции Односторонние приделы Теоремы о пределах функции Замечательные приделы Бесконечно малые и бесконечно большие величины Примеры
Слайд 2Понятие числовой функции
Понятие функцииявляется одним из основных математических понятий, оно связано с установлением зависимости (связи) между элементами двух множеств. Пусть даны два непустых множествадействительных чисел X и У. Соответствие f, котороекаждому данному числу х ∈X сопоставляет одно и только одно число у ∈Y, называется числовой функцией и записывается у = f(x) Говорят еще, что функция fотображает множество X на множество У.
Слайд 3Переменная х называется аргументом функции или независимой переменной, а у — значением функции или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Множество X называется областью определения функции f и обозначается D(f). Множество всех у называется множеством значений функции f и обозначается E(f) Если переменные x и y рассматривать, как декартовы координаты, то графиком функции у = f(x) называется множество точек координатной плоскости ОXY с координатами (x,y).
Слайд 4Способы задания функций
Основные формы аналитического способа задания функции 1) явная форма: функция задается в виде одной или нескольких формул, например ?= ( ? −1) 2 или ?= 1, если ?>0 −1, если ?<0 0, если ?=0 2) неявная форма: функция задается в виде уравнения, например xy-1=0 3) параметрическая форма: значения x и y выражаются через третью величину, называемую параметром, например x=sin t, y=cos t
Слайд 5Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений. Графический способ: задается график функции. Преимуществом графического задания является его наглядность, недостатком — его неточность
Слайд 6Четные и нечетные функции
Функция у = f(x), определенная на множестве D, называется четной, если для любого х ∈Dвыполняются условия -х ∈D и f(-x)=f(x); нечетной, если для любого х ∈D выполняются условия -х ∈D и f(-x)=f(x). График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат. Например, y= x 2 ; y= 1+ x 2 ; y=ln x ; — четные функции; y= sin x ; y= x 3 — нечетные функции; у = х — 1, y= x — функцииобщего вида, т. е. не четные и не нечетные
Слайд 7Периодические функции
Функция y= f(x), определенная на множестве D, называетсяnериодuческойна этом множестве, если существует такое число T>О, что прикаждом х∈D значение (х + Т)∈Dи f(x + Т) = f(x). При этом число Т называетсяnериодомфункции. Если Т - период функции, то ее периодами будут также числа kТ. где k== ±1; ±2, ... Например, для f= sinxпериодами будут числа ±2π; ±4 π; ±6 π, ...Основной период (наименьший положительный) - это период = 2 π.
Слайд 8Ограниченная фунция
Функция f(x) называется ограниченной сверху, если существует такое число M, что для всех значений х∈D выполняется неравенство f(x)≤M, и ограниченной снизу, если существует такое число m, что для всех значений х∈D выполняется неравенство f(x)≥m, Функция, ограниченная и сверху и снизу, называется ограниченной Например, f(x)=x2ограничена снизу, (m=0) и не ограничена сверху, ? ? =−?2 ограничена сверху (M=0)и не ограничена снизу. f(x)= sin(x) ограничена сверху M=1 и снизу m=-1

Слайд 9Монотонная функция
Пусть функция f(x) определена на интервале (a,b); Функция f(x) называется возрастающей на (a,b), если для любой пары значений ? 1 ∈ ?,? , ? 2 ∈ ?,? из неравенства ? 1 < ? 2 следует неравенство ?(? 1 )< ?(? 2 ) Если из неравенства ? 1 < ? 2 следует неравенство ?(? 1 )≤ ?(? 2 ), то функция называется неубывающей Функция f(x) называется убывающейна (a,b), если для любой пары значений ? 1 ∈ ?,? , ? 2 ∈ ?,? из неравенства ? 1 < ? 2 следует неравенство ?(? 1 )> ?(? 2 ) Если из неравенства ? 1 < ? 2 следует неравенство ?(? 1 )≥ ?(? 2 ), то функция называется невозрастающей Возрастающие, не возрастающие, убывающие и неубывающие функции называются монотонными

Слайд 10Обратная функция
Пусть функция y=f(x) - числовая функция с областью определения D(f) и множеством значений E(f) Для любого y0∈ E(f) в множестве D(f) найдется хотя бы одно значение x=x0такое, что f(x0)=y0. Если y=f(x) непрерывная и строго монотонная, то это значение x0 единственное Соответствие, относящее каждому числу y0∈ E(f) единственное число x0∈D(f), называют функцией, обратной к функции f, обозначают символом f-1и пишут x=f-1(y) Чтобы найти функцию, обратную данной, нужно решить уравнение f (х) = yотносительно x. Примеры. 1. Для функции y= 2х обратной функцией является функция x= 1 2 y: 2. Для функции y=x2, x∈[0,∞)обратной функцией является?= ?

Слайд 11Свойства Обратной функции
Если функция x=f-1(y) является обратной для функции y=f(x) , то функция y=f(x) будет обратной для функции x=f-1(y) . Т.е. функции y=f(x) и x=f-1(y) являются взаимно обратными. Область определения функции y=f(x) является множеством значений функции x=f-1(y), а множество значений функции y=f(x) - областью определения функции x=f-1(y) Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости OXY

Слайд 12Сложная функция
Пусть y=f(x) – числовая функция с областью определения D(f) и множеством значений E(f), аz=g(y)– числовая функция с областью определения E(f) и множеством значенийE(g) Соответствие, котороекаждому данному числу х ∈D(f)сопоставляет единственное числоy∈E(f), а этому числу y - единственное числоz∈E(g), называется сложной функцией (или суперпозицией заданных функций, или функцией от функции)и записывается z= g(f(x)) Например , функция z=sin 2x есть суперпозиция двух функцийz=sin y и y=2x
Слайд 13Основные Элементарные функции
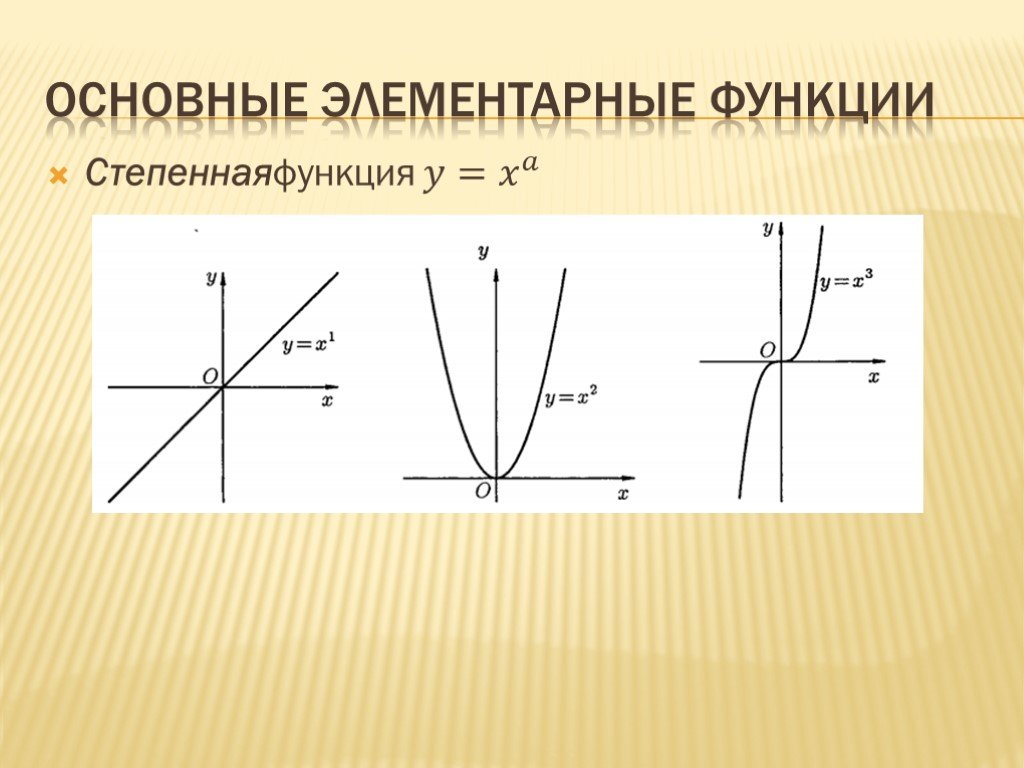
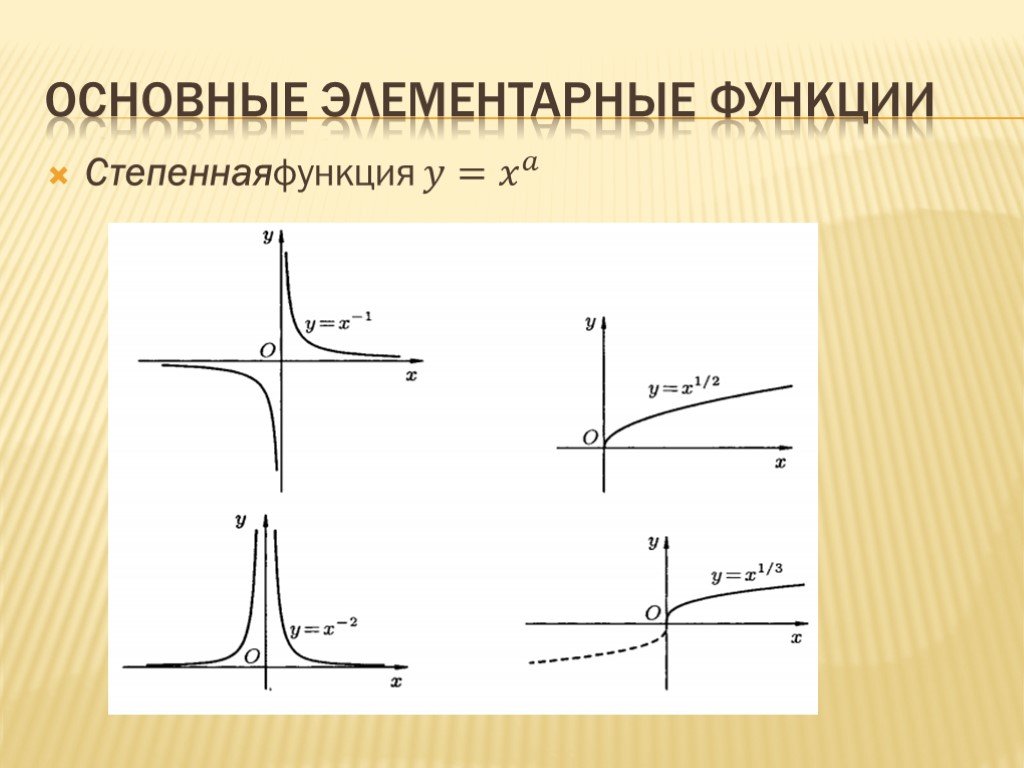
Степеннаяфункция ?= ? ?
Слайд 14
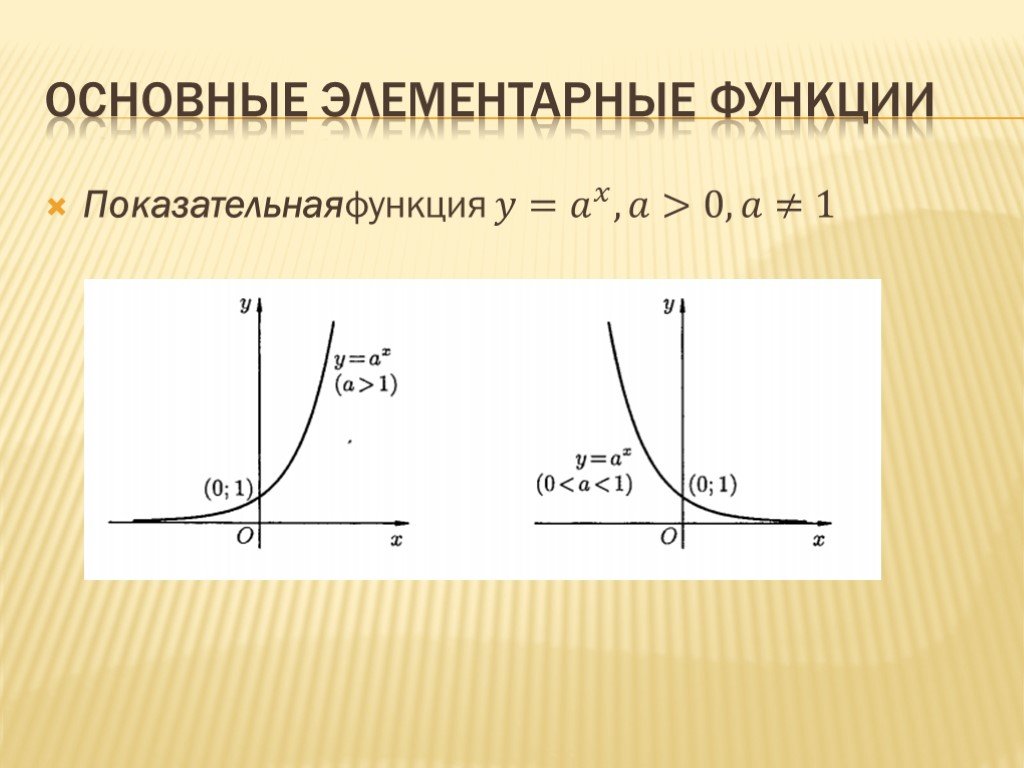
Слайд 15Показательнаяфункция ?= ? ? , ?>0, ?≠1
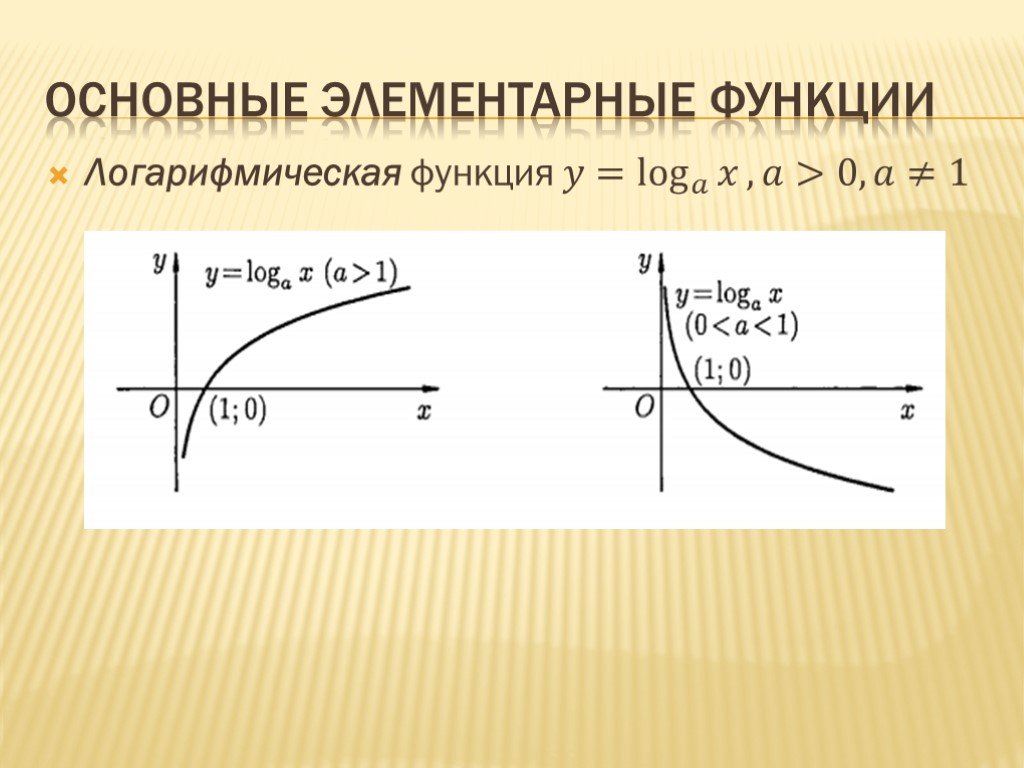
Слайд 16Логарифмическая функция ?= log ? ? ,?>0, ?≠1
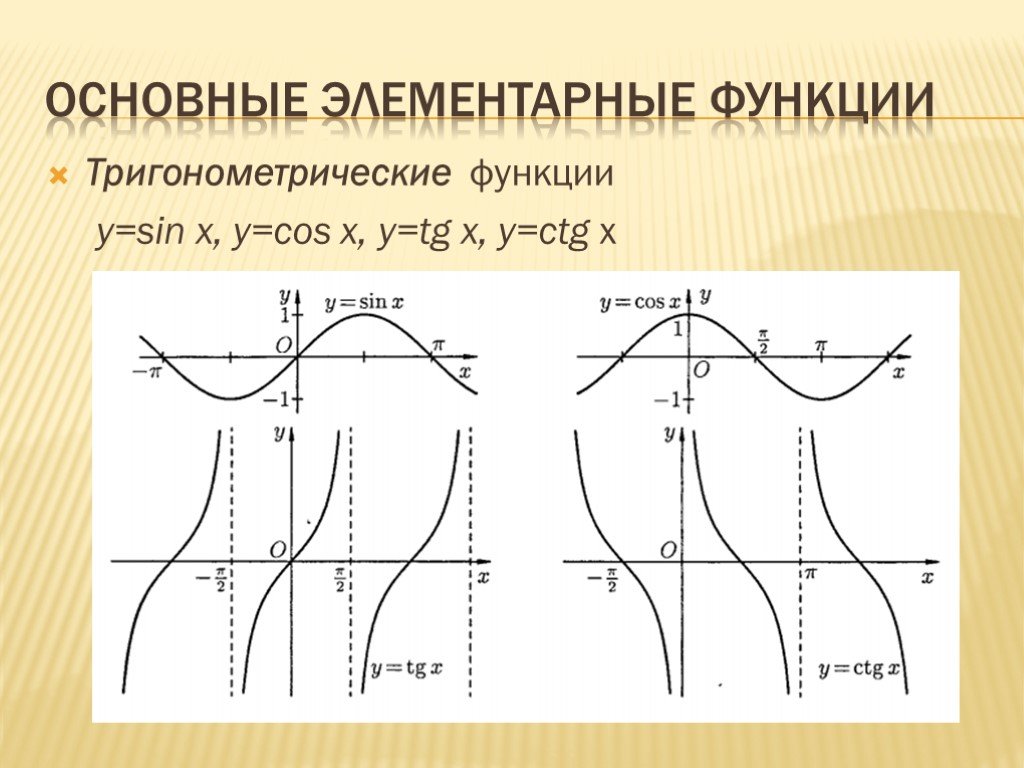
Слайд 17Тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x
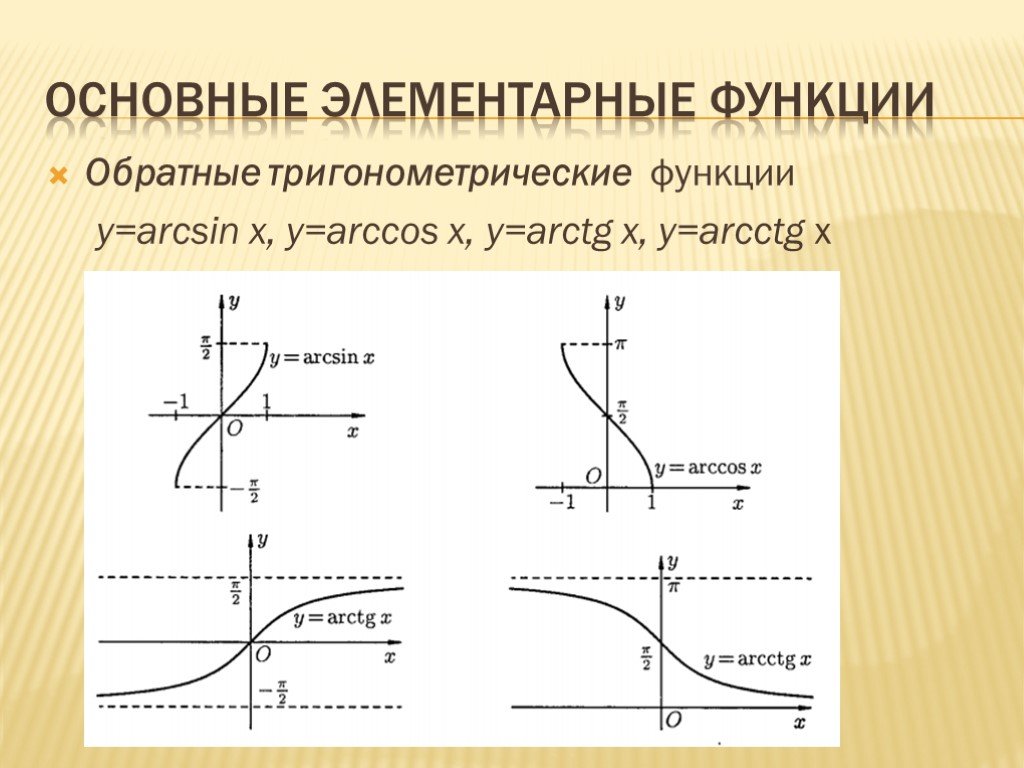
Слайд 18Обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x
Слайд 19Элементарная функция
- эта функция, задаваемая одной формулой , составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и суперпозиций функции Примеры элементарных функций ?= ( ? −1) 2 ;?= ln 2+ ? 3 ;?= sin 2?− ln ? Примеры неэлементарных функций ?= 1, если ?>0 −1, если ?<0 0, если ?=0 ?=?+ ? 2 2 − ? 3 3! + ? 4 4! − ? 5 5! …
Слайд 20Предел функции (по Гейне)
Пусть функция f(x) определена во всех точках промежутка (a,b). Построим последовательность значений аргумента функции f(x) x1,x2,x3…..такую, чтобы все xn∈ (a,b) и последовательность сходилась к x0∈ (a,b) lim ?→∞ ? ? = ? 0 Тогда значения функции f(x) тоже образуют числовую последовательность f(x1), f(x2), f(x3)….. Число Aявляется пределом функции f(x)при x, стремящемся к x0, если для любой последовательности значений аргумента, сходящихся к x0, последовательность значений функции сходится к числу A lim ?→ ? 0 ?(?) =?
Слайд 21Генрих Эдуард Гейне (Heinrich Eduard Heine)
(1821-1881) — немецкий математик. Ученик Дирихле. Изучал математику в Гёттингенском университете, Берлинском университете и в Альбертине в Кёнигсберге, был профессором математики в Бонне и в Галле. Занимался теорией потенциала, теорией функций и дифференциальными уравнениями
Слайд 22Предел функции (по коши)
Число А является пределом функции f(x) при x, стремящемся к x0, lim ?→ ? 0 ?(?) =? если для любого положительного числа ε найдется такое положительное число δ, зависящее от ε, что для всех x ∈ (a,b), удовлетворяющих неравенству 0< ?− ? 0 <δ выполняется неравенство ?(?)−?
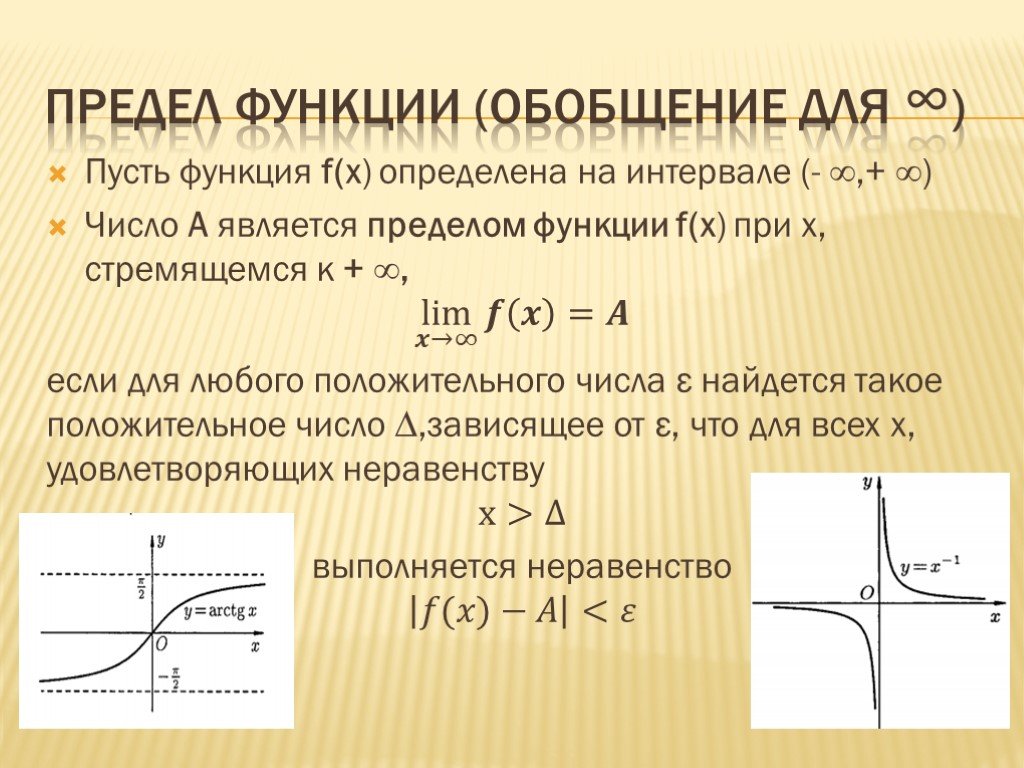
Слайд 23Предел функции (обобщение для ∞)
Пусть функция f(x) определена на интервале (- ∞,+ ∞) Число А является пределом функции f(x) при x, стремящемся к + ∞, lim ?→∞ ? ? =? если для любого положительного числа ε найдется такое положительное число ∆,зависящее от ε, что для всех x, удовлетворяющих неравенству x>∆ выполняется неравенство ?(?)−?
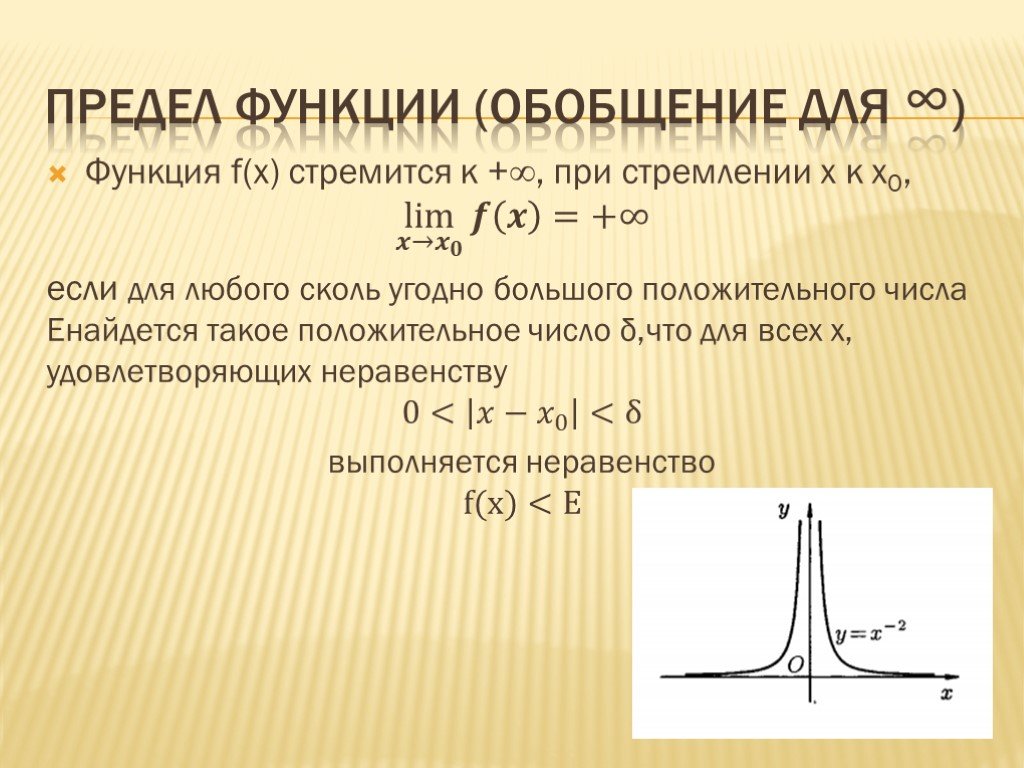
Слайд 24Функция f(x) стремится к +∞, при стремлении x к x0, lim ?→ ? ? ? ? =+∞ если для любого сколь угодно большого положительного числа Eнайдется такое положительное число δ,что для всех x, удовлетворяющих неравенству 0< ?− ? 0 <δ выполняется неравенство f(x)
Слайд 25Односторонние пределы
В определении предела функции lim ?→ ? ? ? ? =А считается, что х стремится к x0любым способом: оставаясь меньшим, чем x0(слева от x0), большим, чем x0(справа от x0), или колеблясь около точки x0 . Бывают случаи, когда способ приближения аргумента xк x0 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов
Слайд 26Пусть f(x) определена на (a,x0) .Число А1является левым пределом функции f(x) при x, стремящемся к x0слева lim ?→ ? 0 −0 ?(?) = ? 1 если для любого положительного числа ε найдется такое положительное число δ, зависящее от ε, что для всех x ∈ (a,x0), удовлетворяющих неравенству ? 0 −?<δвыполняется неравенство ?(?)− ? 1
Слайд 27Пределы функции слева и справа называются одностороннимипределами. Очевидно, если существует lim ?→ ? 0 ?(?) =?, то существуют и оба односторонних предела, причем А = A1= A2 Справедливо и обратное утверждение: если существуют оба предела lim ?→ ? 0 −0 ?(?) = ? 1 и lim ?→ ? 0 +0 ?(?) = ? 2 и они равны, то существует предел lim ?→ ? 0 ?(?) =? Если же A1 ≠ A2,то предел lim ?→ ? 0 ?(?) =? не существует
Слайд 28Теоремы о пределах функций
1) Функция может иметь только один предел 2) Если функции f(x) и g(x) имеют пределы при?→?, то функции? ? ±? ? , ? ? ∙? ? , ?(?) ?(?) также имеют пределы при ?→?, причем lim ?→? ? ? ±? ? = lim ?→? ?(?)± lim ?→? ?(?) lim ?→? ? ? ∙? ? = lim ?→? ?(?)∙ lim ?→? ?(?) lim ?→? ?(?) ?(?) = lim ?→? ?(?) lim ?→? ?(?)
Слайд 29Следствия Теорем о пределах функций
1)Постоянный множитель можно выносить за знак предела: lim ?→ ? 0 с? ? =? lim ?→ ? 0 ?(?) 2) Предел степени с натуральным показателем равен той же степенипредела: lim ?→ ? 0 (? ? ) ? = ( lim ?→ ? 0 ? ? ) ? , в частности lim ?→ ? 0 ? ? = ? 0 ? ,
Слайд 30Пример 1
Вычислить предел lim ?→1 ? 3 +3 ? 2 +5 2? 2 −?+2 = lim ?→1 ? 3 +3 ? 2 +5 lim ?→1 2? 2 −?+2 = lim ?→1 ? 3 + lim ?→1 3 ? 2 + lim ?→1 5 lim ?→1 2? 2 − lim ?→1 ? + lim ?→1 2 = = lim ?→1 ? 3 +3 lim ?→1 ? 2 +5 2 lim ?→1 ? 2 − lim ?→1 ? +2 = ( lim ?→1 ? ) 3 +3 ( lim ?→1 ? ) 2 +5 2 ( lim ?→1 ? ) 2 −1+2 = 1+3+5 2−1+2 = 9 3 =3 - Использованы теоремы о пределе частного, суммы, произведения
Слайд 31Пример 2
Вычислить предел lim ?→3 2 ? 2 −18 ? 2 −2?−3 = lim ?→3 2 (? 2 −9) ? 2 +?−3?−3 = lim ?→3 2(?+3)(?−3) ?(?+1)−3(?+1) = lim ?→3 2(?+3)(?−3) (?+1)(?−3) = = lim ?→3 2(?+3) ?+1 = 12 4 =3 Числитель и знаменатель разложены на множители, дробь преобразована, затем использованы теоремы о пределе частного, суммы, произведения
Слайд 32Пример 3
Вычислить предел lim ?→2 2?−4 2? −2 = lim ?→2 (2?−4)( 2? +2) ( 2? −2)( 2? +2) = lim ?→2 (2?−4)( 2? +2) 2?−4 = = lim ?→2 2? +2 = 4 Числитель и знаменатель дроби умножен на выражение, сопряженное знаменателю, дробь преобразована, затем использованы теоремы о пределе частного, суммы, произведения
Слайд 33Замечательные приделы
В теории пределов важное место занимают следующие пределы, с помощью которых вычисляются многие пределы от элементарных функций: 1) lim ?→0 sin ? ? =1 2) lim ?→0 (1+?) 1 ? = lim ?→∞ (1+ 1 ? ) ? =? 3) lim ?→0 log ? (1+?) ? = log ? ? , lim ?→0 ln (1+?) ? =1, 4) lim ?→0 ? ? −1 ? = ln ? , lim ?→0 ? ? −1 ? =1, 5) lim ?→0 (1+?) ? −1 ? =?
Слайд 34Пример 4
Вычислить предел lim ?→0 sin ? + sin 3? sin ? − sin 2? = lim ?→0 sin ? + 3sin ?−4 sin 3 ? sin ? − 2sin ? cos ? = = lim ?→0 4 sin ?( 1− sin 2 ? ) sin ? (1− 2 cos ? ) = lim ?→0 4 cos ? 1− 2 cos ? = 4 −1 =−4 Использованытригонометрические формулы двойного и тройного угла, преобразование дроби и первый замечательный придел
Слайд 35Бесконечно большие функции
Функция f(x) называется бесконечно большой функцией (ББФ) при ?→?, если для любого сколь угодно большого положительного числа Eнайдется такое положительное число δ,что для всех x, удовлетворяющих неравенству 0< ?−? <δ выполняется неравенство |f x |
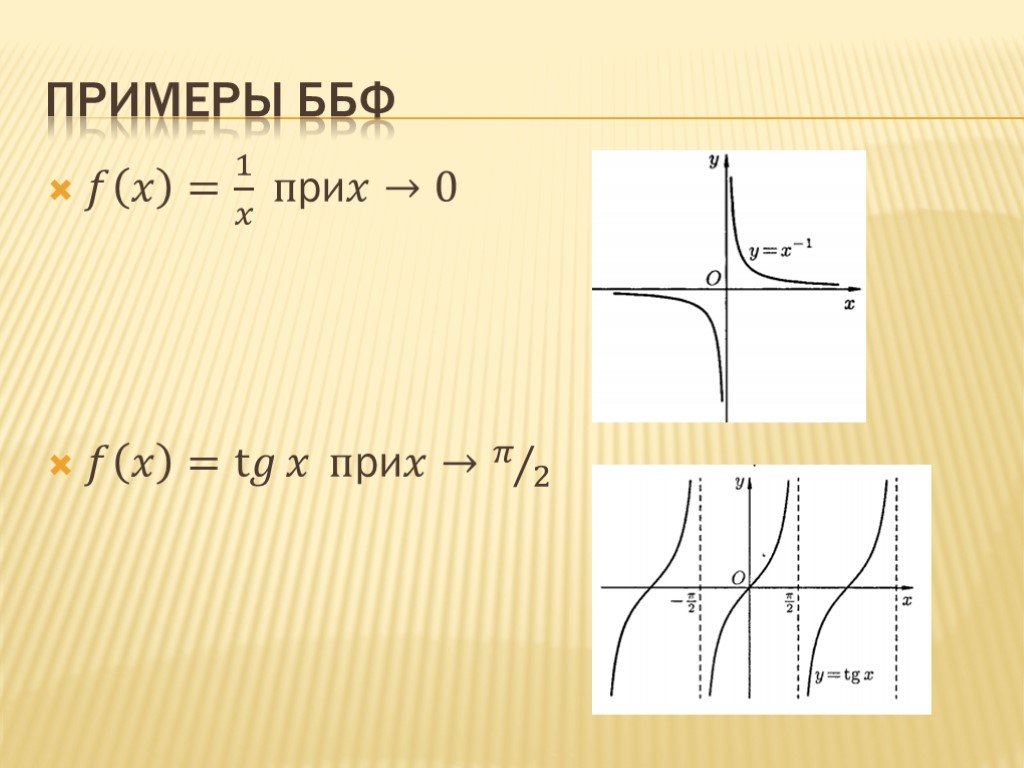
Слайд 36Примеры Ббф
? ? = 1 ? при?→0 ? ? = t? ? при?→ ? 2
Слайд 37Бесконечно малые функции
Функция f(x) называется бесконечно малой функцией (БМФ)при ?→?, если для любого сколь угодно малого положительного числа εнайдется такое положительное число δ,что для всех x, удовлетворяющих неравенству 0< ?−? <δ выполняется неравенство |f x |<ε Т.е. если f(x) стремится к 0, при стремлении x к a lim ?→? ? ? =?
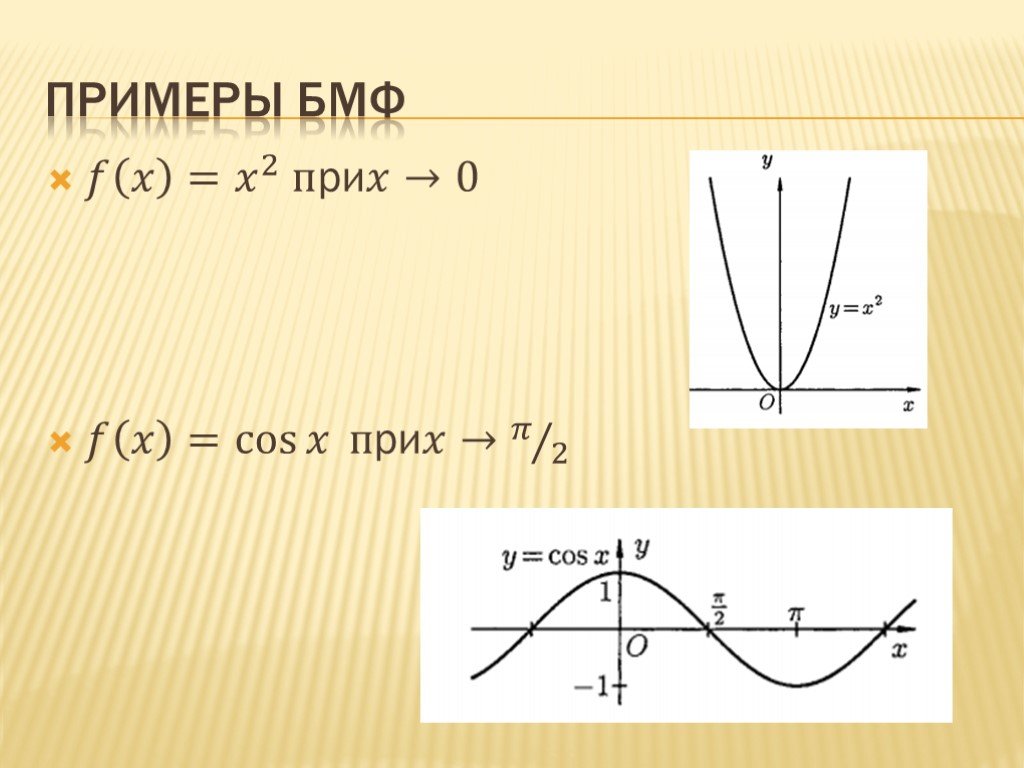
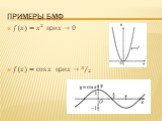
Слайд 38Примеры Бmф
? ? = ? 2 при?→0 ? ? = cos ? при?→ ? 2
Слайд 39Теоремы о бесконечно малых функциях
1) Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция 2) Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция Следствие 1 Произведение двух БМФ есть БМФ Следствие 2 Произведение БМФ на число БМФ 3) Частное от деления бесконечномалой функции на функцию, имеющую отличный от нуля предел, есть бесконечно малая функция 4) Если функция a(x)— бесконечно малая (?≠0), то функция 1 ?(?) есть бесконечно большая функция и наоборот: если функция f{x) — бесконечнобольшая, 1 ?(?) — бесконечно малая
Слайд 40Сравнение бесконечно малых функций
Две БМФ сравниваются между собой с помощью их отношения. Как известно, сумма, разность и произведение двух БМФ. есть БМФ. Отношение же двух БМФ может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Слайд 41Пусть ?=? ? и ?=? ? −две БМФ при ?→ ? 0 . lim ?→ ? ? ? ? =?, lim ?→ ? ? ? ? =? 1) Если lim ?→ ? ? ? ? =?≠? , то ? и ?- бесконечно малые одного порядка 2) Если lim ?→ ? ? ? ? =? , то ? - бесконечно малая более высокого порядка, чем ? 3) Если lim ?→ ? ? ? ? =∞ , то ? - бесконечно малая более низкого порядка,чем ? 4) Если lim ?→ ? ? ? ? не существует, то ? и ?- несравнимые бесконечно малые
Слайд 42Эквивалентные бесконечно малые функции
Если lim ?→ ? ? ? ? =? , то ? и ?- эквивалентные бесконечно малые ?~? эквивалентные бесконечно малые играют особую роль среди БМФ одного порядка Т.1. Предел отношения двух БМФ не изменится, если каждую или одну из них заменить эквивалентной ей БМФ. Т.2. Разность двух эквивалентных БМФ есть БМФ более высокого порядка, чем каждая из них. Т.3, Сумма конечного числа БМФ разных порядков эквивалентна слагаемому низшего порядка.
Слайд 43Основные Эквивалентные бесконечно малые функции
Слайд 44Пример 5
Вычислить предел lim ?→0 t? 2? sin 3? Так как sin 3? ~3? и t? 2?~2? , то lim ?→0 t? 2? sin 3? = lim ?→0 2? 3? = 2 3