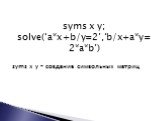Презентация "Решение нелинейных уравнений в системе matlab" – проект, доклад
Презентацию на тему "Решение нелинейных уравнений в системе matlab" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение уравнений с помощью численных методов
метод половинного деления (дихотомии) предназначенный для нахождения корней уравнений, представленных в виде f(x)=0. Пусть непрерывная функция f(x) ...Решение возвратных уравнений
Способы решения уравнений высших степеней. Разложение многочлена на множители. Метод замены переменной. Функционально-графический метод. . Возвратные ...Решение тригонометрических уравнений при помощи формулы понижения степени.
Гипотеза. На уроках математики мы прошли тригонометрические формулы, а так же рассмотрели методы решения тригонометрических уравнений, среди которых ...Решение задач по теме: Призма.
. Решение к 1-ой задаче. В основании правильной четырехугольной призмы – квадрат и боковое ребро призмы перпендикулярно основанию. S=2Sosnov+Sbok ...Решение задач по теме: «Магнитная индукция, самоиндукция
Основные законы и формулы. Закон электромагнитной индукции (закон Фарадея) ЭДС индукции в движущемся проводнике B – магнитная индукция однородного ...Решение задач по теме «Длина волны. Скорость распространения волн»
Пример оформления домашних задач. Дано: Решение: λ=2м ν=1,5 Гц v-? ?= 1 ? ?=??= ? ? ⟹?=?? ?=2м∗1,5 Гц=3м/с Ответ: 3м/с. 1. Волна распространяется ...Вендинговая торговля в системе образования потребительской кооперации
Актуальность. Вендинговый бизнес давно зарекомендовал себя как быстро окупаемый и высокорентабельный. Если выбрать правильное месторасположения, вложенные ...Сущность и задачи шоу-бизнеса в системе предпринимательства
Определение панятия Шоу-бизнеса. Шоу –бизнес –это в переводе с английского языка «show» и «business» трактует следующим образом: «Шоу - пышное сценическое ...Решение бизнес-кейса“burger king”
Общая стратегия. Позиционирование: ”Крутой Воппер” Запуск мобильных приложений SMM Event-marketing Вирусный маркетинг. Площади реализации. Потребительские ...профориентация в системе школьного образования
. . Факторы, влияющие на выбор профессии школьниками средней общеобразовательной школы. Проблема профессионального самоопределения у старшеклассников ...Реклама в системе маркетинга
Реклама используется для ускорения и облегчения процесса покупки и продажи. Товары, различные по своему назначению, по-разному рекламируются. Группа ...Нормативные документы в системе образования России
Государственная программа «Развитие образования» на 2013-2020 годы. Прогноз развития сферы образования на период до 2020 года Особенностью сети организаций ...Менеджеры в системе управления
Менеджер – это человек, занимающий постоянную управленческую должность и наделенный полномочиями принимать решения по определенным видам деятельности ...Коммуникации в системе менеджмента
Информационно-коммуникационное обеспечения менеджмента. Специфика коммуникологических исследований Процедура коммуникологического исследования представляет ...Роль коммуникаций в системе управления
. Понятие коммуникации. Коммуникация — это общение, в процессе которого происходит обмен информацией, мыслями и эмоциями между двумя или более людьми ...Решение задач по количественным взаимосвязям в энергообеспеченности мышечной деятельности
Домашнее задание:. Физиология возбудимых тканей. Основные формулы и табличные значения. СВ = ЧСС х СО ЛВ = ЧД х ДО Е = ПО2 х КЭК АВРо2 = рО2А – рО2В ...Стратегические и тактические планы организации в системе менеджмента
Практическое занятие № 3. Решение ситуационных задач по теме «Стратегические и тактические планы организации в системе менеджмента». Ситуационная ...Решение задач по теме : «Касательная к окружности»
Устно:. Что называется окружностью? Что называется диаметром окружности? Что называется хордой? Что называется касательной к окружности? Что называется ...Элементы v группы, главной подгруппы периодической системе элементов Д.И Менделеева
Азот (N) 2s22p3 Фосфор (P) 3s23p3 Мышьяк (As) 3d104s24p3 Сурьма (Sb) 4d105s25p3 Висмут (Bi) 4f145d106s26p3. Электронное строение:. уменьшаются. Степени ...Алгоритм построения модели вала в системе КОМПАС
Алгоритм построения модели вала. Исходные данные для вала. Запускаем графический редактор и создаем новый документ Деталь. Устанавливаем свойства ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 июля 2019
Категория:Разные
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию


























![conv(p1, р2) - вычисляет произведение двух полиномов; deconv(pl, р2) -осуществляет деление полинома p1 на полином р2 polyval(p1, х) - вычисляет значение полинома с коэффициентами p1 в точке х; polyder (p1 [, р2]) - вычисляет производную от полинома. Функции для действий над полиномами conv(p1, р2) - вычисляет произведение двух полиномов; deconv(pl, р2) -осуществляет деление полинома p1 на полином р2 polyval(p1, х) - вычисляет значение полинома с коэффициентами p1 в точке х; polyder (p1 [, р2]) - вычисляет производную от полинома. Функции для действий над полиномами](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen5.jpg)
![Решить алгебраическое уравнение в Matlab можно при помощи встроенной функции roots(p). Она формирует вектор, элементы которого являются корнями полинома с коэффициентами “p” Общий вид: r = roots(p), где p=[p1 p2 ... pn pn+1]. Функция roots(p) Решить алгебраическое уравнение в Matlab можно при помощи встроенной функции roots(p). Она формирует вектор, элементы которого являются корнями полинома с коэффициентами “p” Общий вид: r = roots(p), где p=[p1 p2 ... pn pn+1]. Функция roots(p)](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen6.jpg)
![p = [1 3 5 7] r = roots(p) Результат: Вычислим корни полинома: p(x) = x3 + 3x2 + 5x +7 p = [1 3 5 7] r = roots(p) Результат: Вычислим корни полинома: p(x) = x3 + 3x2 + 5x +7](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen7.jpg)



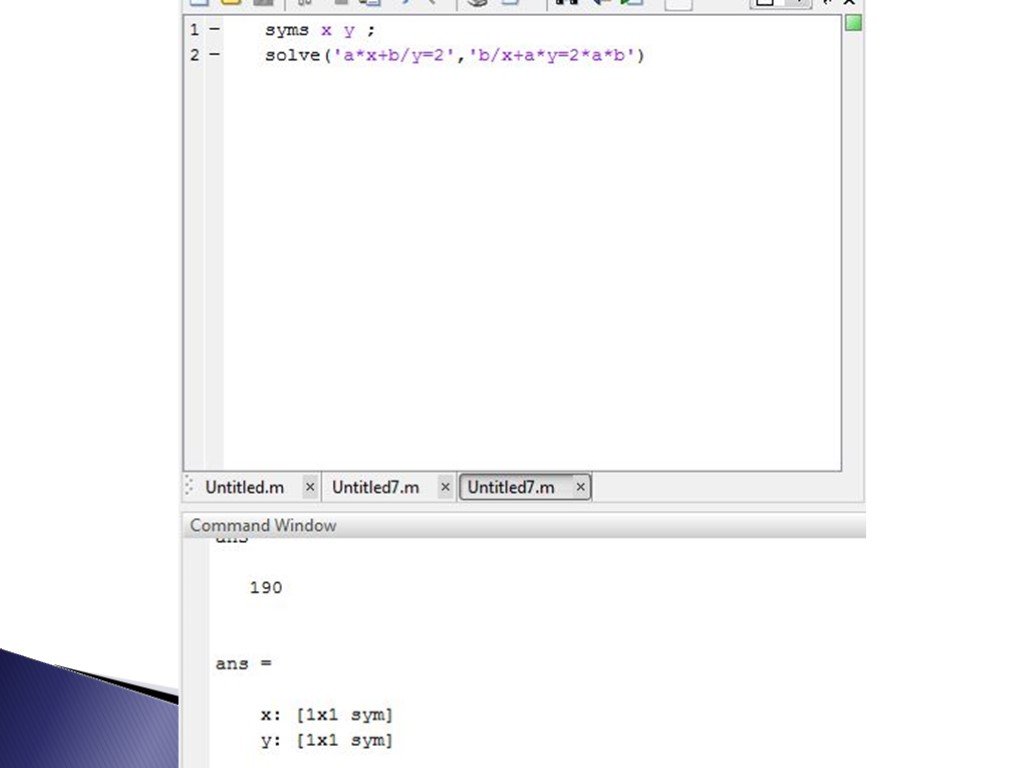
![A=[-5/3 -1 -2/3; -5/6 1/4 11/12; 1/6 -17/4 -19/12] p=poly(A) r=roots(p) p=poly(r) A=[-5/3 -1 -2/3; -5/6 1/4 11/12; 1/6 -17/4 -19/12] p=poly(A) r=roots(p) p=poly(r)](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen12.jpg)



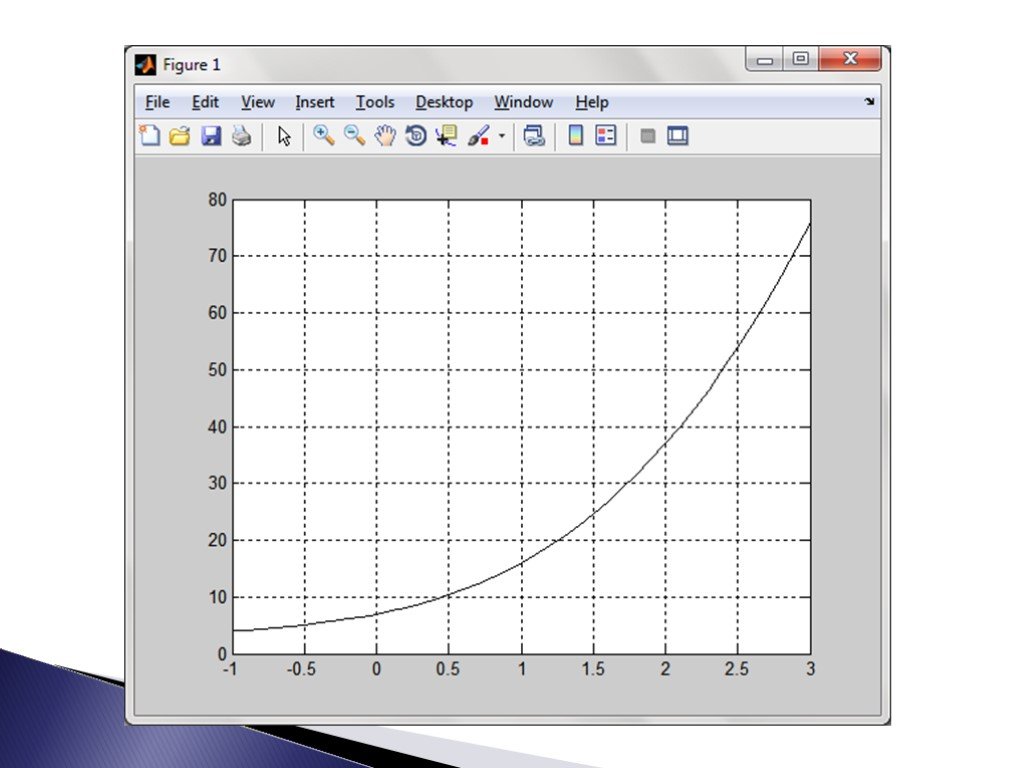
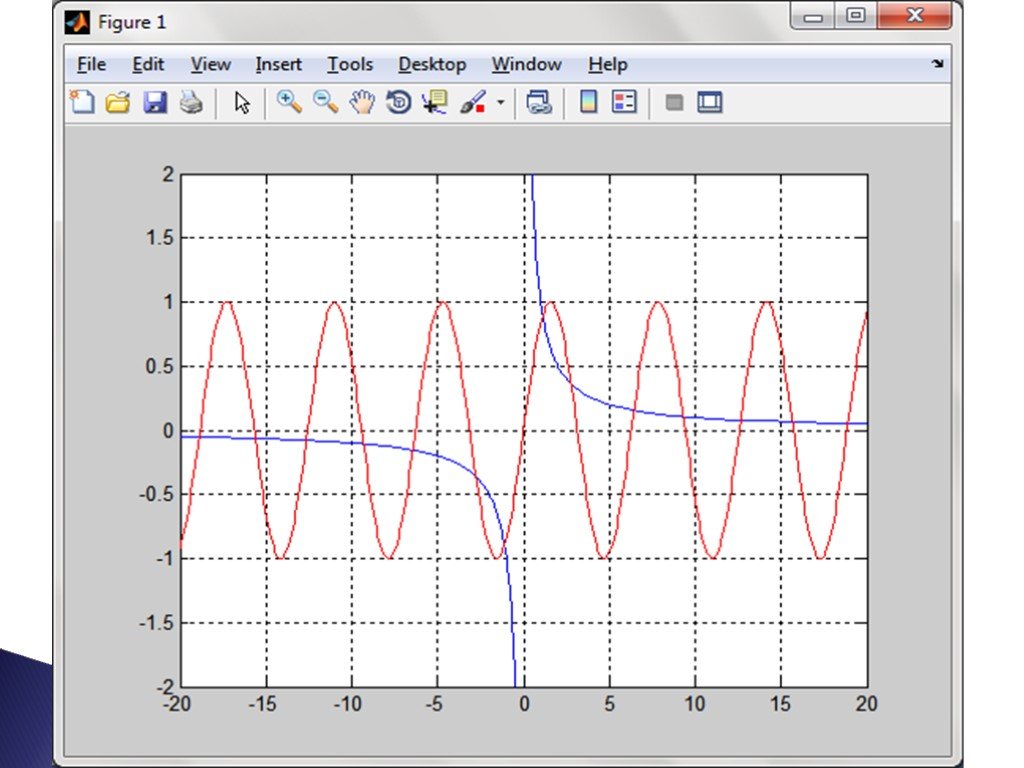
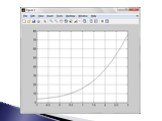
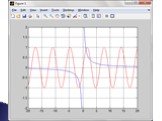
![Построим графики в Matlab с помощью функции fplot: figure axes fplot('1/x', [-20 -0.5]) hold on fplot('1/x', [0.5 20]) fplot('sin(x)', [-20 20], 'r') grid on Построим графики в Matlab с помощью функции fplot: figure axes fplot('1/x', [-20 -0.5]) hold on fplot('1/x', [0.5 20]) fplot('sin(x)', [-20 20], 'r') grid on](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen16.jpg)


![x = fzero(@cos,[1 2]) Результат: x = 1.5708. Найти нуль функции cos между 1 и 2 x = fzero(@cos,[1 2]) Результат: x = 1.5708. Найти нуль функции cos между 1 и 2](https://prezentacii.org/upload/cloud/19/07/156359/images/thumbs/screen20.jpg)