Презентация "Решение уравнений с помощью численных методов" – проект, доклад
Презентацию на тему "Решение уравнений с помощью численных методов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение нелинейных уравнений в системе matlab
Научиться решать в Matlab алгебраические и трансцендентные уравнения Ознакомление с такими функциями как fzero, poly, roots и solve Изучение нелинейных ...Решение тригонометрических уравнений при помощи формулы понижения степени.
Гипотеза. На уроках математики мы прошли тригонометрические формулы, а так же рассмотрели методы решения тригонометрических уравнений, среди которых ...Решение возвратных уравнений
Способы решения уравнений высших степеней. Разложение многочлена на множители. Метод замены переменной. Функционально-графический метод. . Возвратные ...Эвристический метод как один из методов принятия управленческих решений
Разработка управленческих решений для нетиповых, творческих задач — довольно трудное занятие. В управленческой практике таких задач довольно много. ...Решение задач по теме: Призма.
. Решение к 1-ой задаче. В основании правильной четырехугольной призмы – квадрат и боковое ребро призмы перпендикулярно основанию. S=2Sosnov+Sbok ...Решение задач по теме: «Магнитная индукция, самоиндукция
Основные законы и формулы. Закон электромагнитной индукции (закон Фарадея) ЭДС индукции в движущемся проводнике B – магнитная индукция однородного ...Решение задач по теме «Длина волны. Скорость распространения волн»
Пример оформления домашних задач. Дано: Решение: λ=2м ν=1,5 Гц v-? ?= 1 ? ?=??= ? ? ⟹?=?? ?=2м∗1,5 Гц=3м/с Ответ: 3м/с. 1. Волна распространяется ...Решение задач по теме : «Касательная к окружности»
Устно:. Что называется окружностью? Что называется диаметром окружности? Что называется хордой? Что называется касательной к окружности? Что называется ...Решение задач по количественным взаимосвязям в энергообеспеченности мышечной деятельности
Домашнее задание:. Физиология возбудимых тканей. Основные формулы и табличные значения. СВ = ЧСС х СО ЛВ = ЧД х ДО Е = ПО2 х КЭК АВРо2 = рО2А – рО2В ...Решение бизнес-кейса“burger king”
Общая стратегия. Позиционирование: ”Крутой Воппер” Запуск мобильных приложений SMM Event-marketing Вирусный маркетинг. Площади реализации. Потребительские ...Обзор эндоскопических методов исследования
План презинтации:. 1. Введение 2. Виды эндоскопов 3. Блок-схема современного эндоскопа 4. Промышленные модели приборов. Введение. ЭНДОСКОПИЯ - метод ...Методика обучения детей старшего дошкольного возраста измерению объемов сыпучих и жидких веществ с помощью условной меры
Основная задача. Формирование представлений об общих способах измерения. При измерении объемов используются те же общие правила, что и при измерении ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 сентября 2019
Категория:Разные
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию


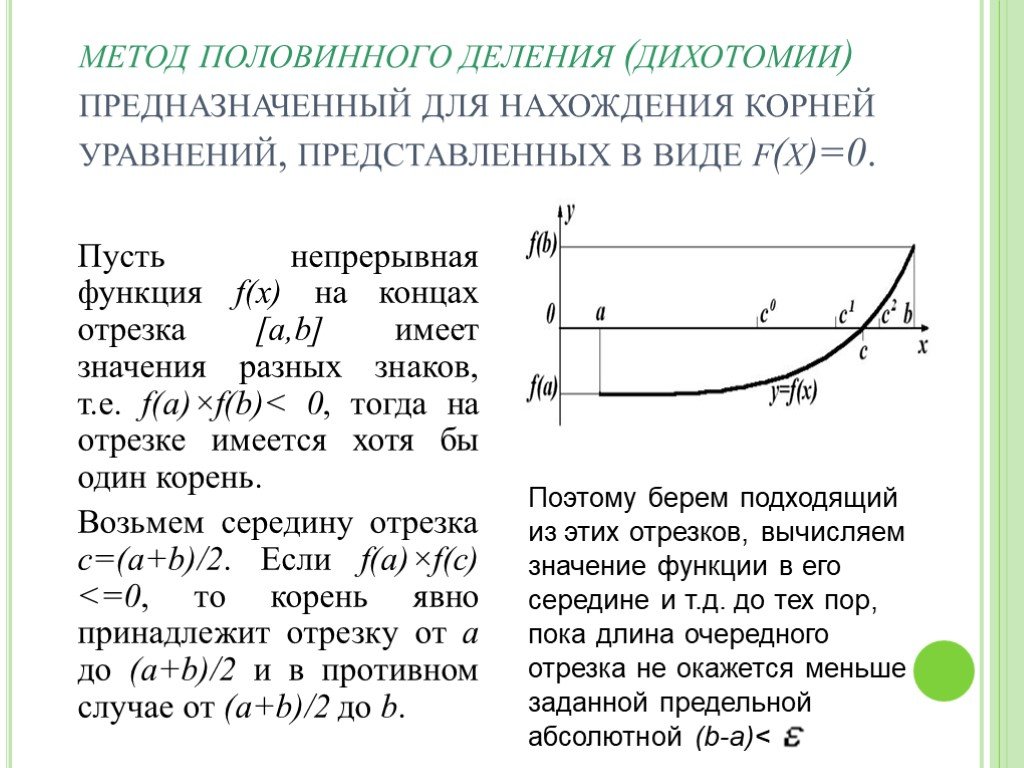










![метод половинного деления (дихотомии) предназначенный для нахождения корней уравнений, представленных в виде f(x)=0. Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0, тогда на отрезке имеется хотя бы один корень. Возьмем середину отрезка с=(a+ метод половинного деления (дихотомии) предназначенный для нахождения корней уравнений, представленных в виде f(x)=0. Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0, тогда на отрезке имеется хотя бы один корень. Возьмем середину отрезка с=(a+](https://prezentacii.org/upload/cloud/19/09/161353/images/thumbs/screen2.jpg)
![метод половинного деления. Так как каждое очередное вычисление f(c) сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешности количество вычислений n определяется условием (b-a)/2n< , или n~log2((b-a)/ ). Например, при исходном единичном интервале и точности порядка 6 з метод половинного деления. Так как каждое очередное вычисление f(c) сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешности количество вычислений n определяется условием (b-a)/2n< , или n~log2((b-a)/ ). Например, при исходном единичном интервале и точности порядка 6 з](https://prezentacii.org/upload/cloud/19/09/161353/images/thumbs/screen3.jpg)

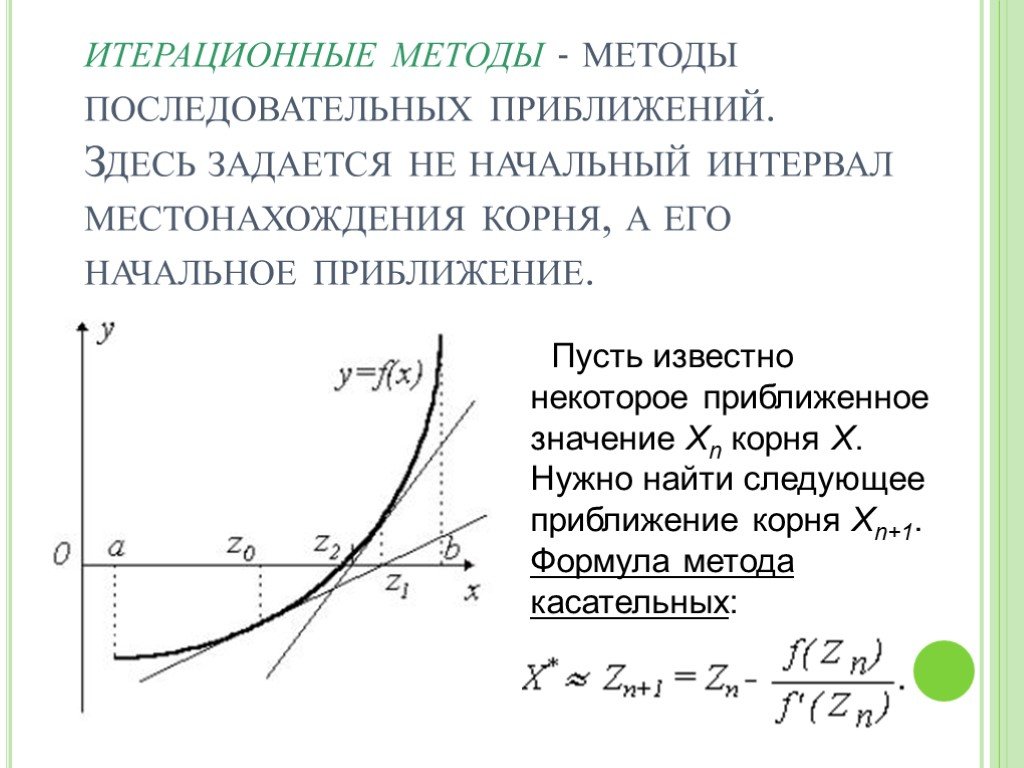
![В качестве исходной точки х выбирается тот конец интервала [a,b], которому ордината того же знака, что и знак второй производной, т.е. —x = a или — х = b. Корень можно найти с любой степенью точности е. это означает, что . Если производная функции мало изменяется в окрестности корня, то можно исполь В качестве исходной точки х выбирается тот конец интервала [a,b], которому ордината того же знака, что и знак второй производной, т.е. —x = a или — х = b. Корень можно найти с любой степенью точности е. это означает, что . Если производная функции мало изменяется в окрестности корня, то можно исполь](https://prezentacii.org/upload/cloud/19/09/161353/images/thumbs/screen5.jpg)

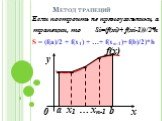
![Определённый интеграл. Можно трактовать как площадь подынтегральной функции (криволинейной трапеции) на отрезке [a;b]. x у 0 f(x) a b = S Определённый интеграл. Можно трактовать как площадь подынтегральной функции (криволинейной трапеции) на отрезке [a;b]. x у 0 f(x) a b = S](https://prezentacii.org/upload/cloud/19/09/161353/images/thumbs/screen7.jpg)

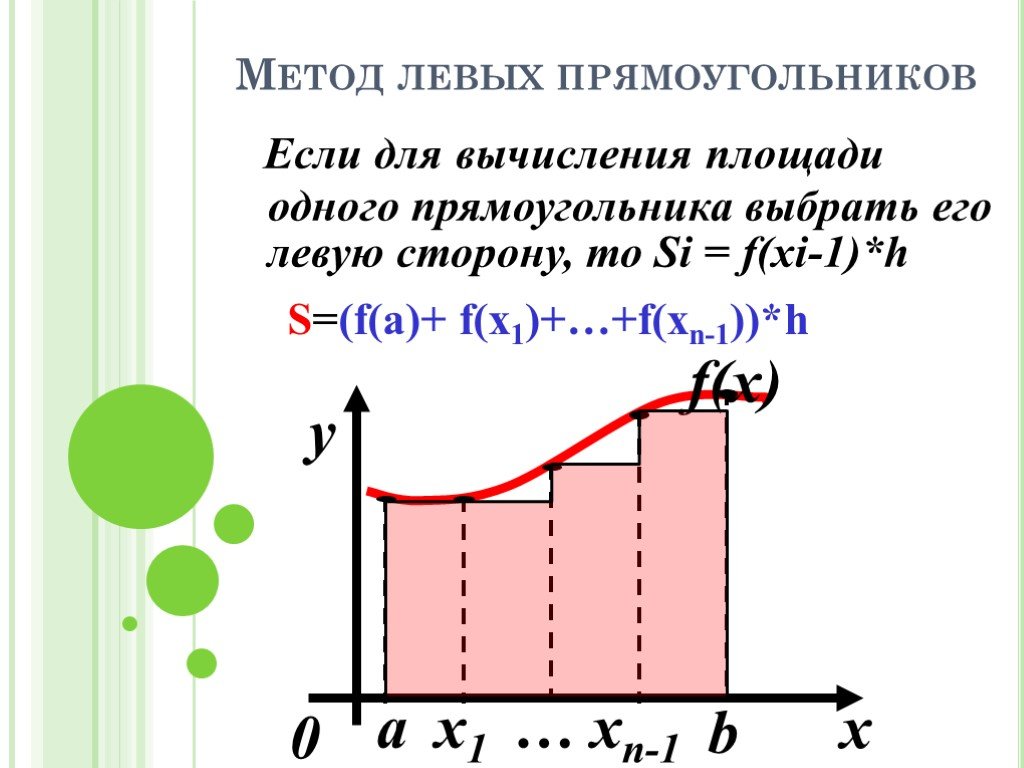
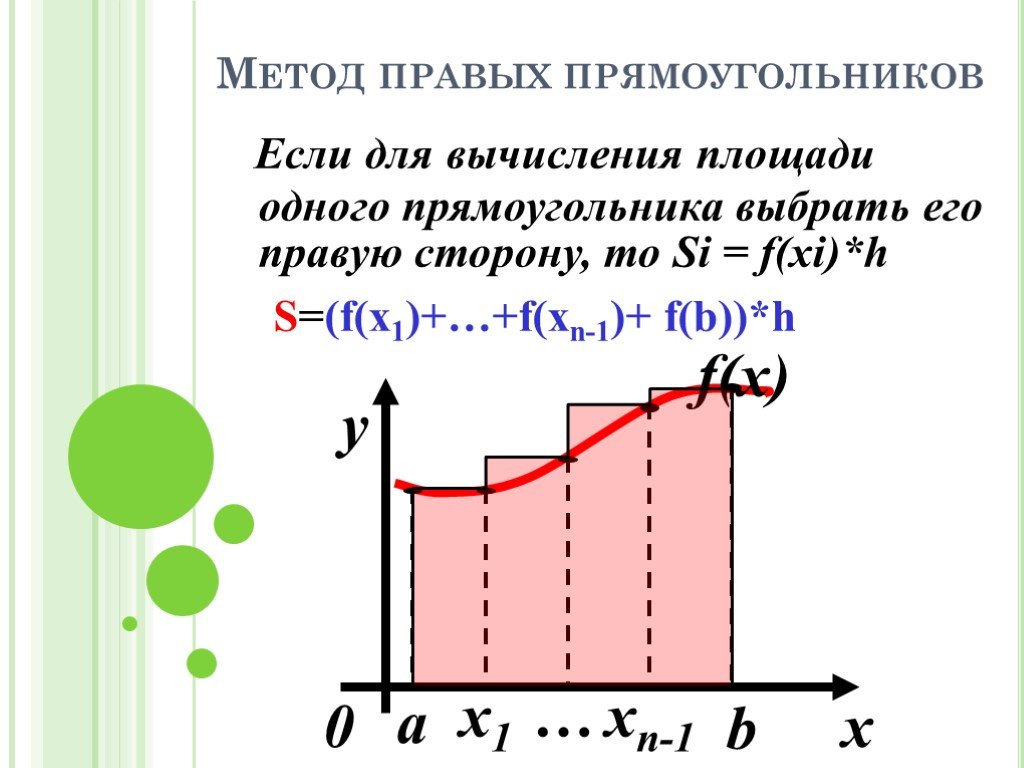
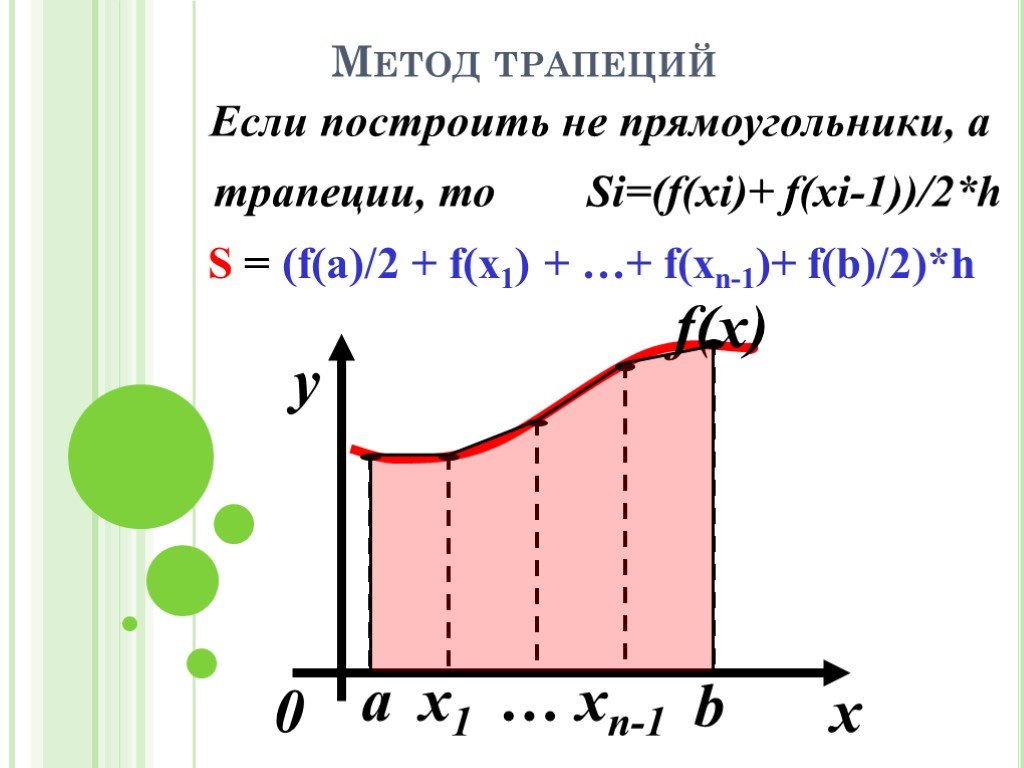
![Пусть функция f(x) определена на отрезке [а;b]. Требуется: приближенно вычислить определённый интеграл. Суть метода: разобьём отрезок [а,b] на n равных отрезков длины h=(b-a)/n, разрезая фигуру под функцией f(x) на n полосок, считая их прямоугольниками. Тогда S Si , при n Si S Пусть функция f(x) определена на отрезке [а;b]. Требуется: приближенно вычислить определённый интеграл. Суть метода: разобьём отрезок [а,b] на n равных отрезков длины h=(b-a)/n, разрезая фигуру под функцией f(x) на n полосок, считая их прямоугольниками. Тогда S Si , при n Si S](https://prezentacii.org/upload/cloud/19/09/161353/images/thumbs/screen9.jpg)