Презентация "Приключения в стране графов" (5 класс) по русскому языку – проект, доклад
Презентацию на тему "Приключения в стране графов" (5 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Русский язык. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Безударные гласные в корне
А1. Укажите слово, написание которого проверяется ударением. 1) Пр_красный; 2) смерка_тся; 3) велос_пед; 4) р_скошный. А2. Укажите слово с непроверяемой ...Безударная гласная в корне слова
План урока. Повторить правило Словарная работа Отрабатывать умение подбирать проверочные слова Проверочная работа Домашнее задание. Как проверить ...Безударная гласная в корне слова и ее проверка
Пояснительная записка. Тренажер содержит 9 упражнений для фронтальной и индивидуальной работы. При выполнении нужно не перебирать варианты ответов, ...Англицизмы в речи русского делового человека
Цель:. данной работы состоит в том, чтобы изложить роль англицизмов в деловом сленге русского человека. Цель определила конкретные задачи:. изложить ...Архаизмы и историзмы в русском языке
Эпиграфы. Берегите наш язык, наш прекрасный русский язык, — это клад, это достояние, переданное нам нашими предшественниками! Обращайтесь почтительно ...Безударные гласные в корне слова
Тренажер по русскому языку «Правописание безударных гласных в корне слова» Автор: Разумнова Елена Викторовна. Собери корзину овощей и фруктов! К…ПУСТА ...Алгоритмы в стихах - Создание блок - схем
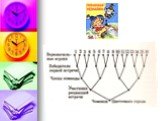
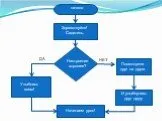
Алгоритмы в стихах. Создание блок-схем. Алгоритм – конечная последовательность шагов в решении задачи, приводящая от исходных данных к требуемому ...«Путешествие мышонка Шуши» Автоматизация звука Ш в слогах, словах, фразах
Я мышонок Шуша, я иду искать мою сестренку Машу. Помогите мне ее найти. Надуем воздушный шар и отправимся в полет. Дыхательная гимнастика. Вдох носом ...А - О в корнях с чередованием
Распредели слова в два столбика. Озарение, отбирать, касаться, казаться, переложу, вскопать, умножение, вымокший, горняцкий, горелый, полагается, ..."Чистописание" в начальной школе
Содержание. Урок № 1 Урок № 12 Урок № 23 Урок № 2 Урок № 13 Урок № 24 Урок № 3 Урок № 14 Урок № 25 Урок № 4 Урок № 15 Урок № 26 Урок № 5 Урок № 16 ...«О, Е» после шипящих и Ц в суффиксах и окончаниях имён существительных
Вежливый, старательный, Скромный и внимательный, Добрый, умный, справедливый, И весёлый, и счастливый. Сказка про шипящие буквы. Дружно живут согласные ..."Чистописание" в начальной школе
Содержание. Урок № 1 Урок № 12 Урок № 23 Урок № 2 Урок № 13 Урок № 24 Урок № 3 Урок № 14 Урок № 25 Урок № 4 Урок № 15 Урок № 26 Урок № 5 Урок № 16 ..."Иностранцы" в нашей речи
Определить роль и место иноязычных слов в современном русском языке. Цель работы. 1. Собрать воедино, проанализировать и обобщить имеющуюся в справочной ...-Н и -НН в суффиксах прилагательных
"Толковые ребята". Правило Опорный конспект Словообразование Лексическая работа Распределительный диктант 1, 2 Игра «Четвертый лишний» Тест Объяснительный ...Безударные гласные в корне слов
цели. Формирование грамотного письма, используя алгоритм проверки безударных гласных в корне слов. понаблюдаем. Под ударением ДОМ,СОВЫ Без ударения ...А – О в корнях –рос - - раст - ( - ращ -), -лаг- -лож-
Выразительно прочитайте стихотворение Н. Забила. Спишите, вставьте пропущенные буквы, объясните их написание. Р…сти, р…сти , яблонька! Подр…стай! ...Безударные гласные в корне слова
Проверяемая безударная гласная корня – одна из самых сложных для учащихся орфограмм, несмотря на внешнюю легкость правила, регулирующего ее написание. ...Аббревиатура и сокращения слов в деловом письме
АББРЕВИАТУРА -. сложносокращённое слово, образованное из начальных букв (например: РФ), звуков (например: вуз) словосочетания или его начальных элементов ...Безударные личные окончания глаголов в настоящем и будущем времени
Цели урока. 1.Формировать у учащихся умение писать безударные личные окончания глаголов. 2. Развивать умение соотносить безударные окончания глаголов ...Автоматизация [Л] в конце слова
вол. пол. стол. чехол. щегол. футбол. стул. мускул. колокол. котел. ...Конспекты
Безударные гласные в корне слова, проверяемые ударением
Автор: Коломейцева Татьяна Ивановна. Место работы: МБОУ лицей № 1 г.Пролетарска Ростовской области. Должность: учитель русского языка и литературы. ...Безударные гласные в падежных окончаниях имён существительных
Тема:. Безударные гласные в падежных окончаниях имён существительных. . Цель:. - . обобщить знания учащихся о постоянных и непостоянных признаках ...Буква е - в начале слов и после гласных; после согласных
Методический паспорт:. Тема урока. :. Буква е - в начале слов и после гласных; после согласных. Цель урока. :. Продолжить ознакомление учащихся ...Безударные гласные в корне слова
Учебно-методическая система «Планета Знаний». Учитель:. Путина Анна Викторовна, учитель начальных классов МБОУ «СОШ № 1» г. Энгельса Саратовской ...Большая буква в кличках животных
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 43». . «Большая буква в кличках животных». ...Большая буква в начале предложения. А.Суконцев «Как ежик шубку менял
Грамота 1 класс. Тема:. Большая буква в начале предложения. А.Суконцев «Как ежик шубку менял». . Задачи урока:. 1 .Закрепить знания об обозначении ...Автоматизация звука [Р] в слогах, словах и предложениях
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа № 7» аула Панахес. Тахтамукайского района Республики Адыгея. ...Большая буква в именах собственных
Учитель начальных классов Федорова Валентина Анатольевна. . Муниципальное общеобразовательное учреждение. «Пятницкая средняя общеобразовательная ...Автоматизация звука [р] в словах
Муниципальное дошкольное образовательное учреждение. «Детский сад компенсирующего вида № 26» . Конспект урока на тему «Автоматизация ...Автоматизация звука [р] в слогах, словах
Муниципальное бюджетное дошкольное образовательное учреждение. детский сад компенсирующего вида № 30 «Лукоморье». . муниципального образования ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 сентября 2019
Категория:Русский язык
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию



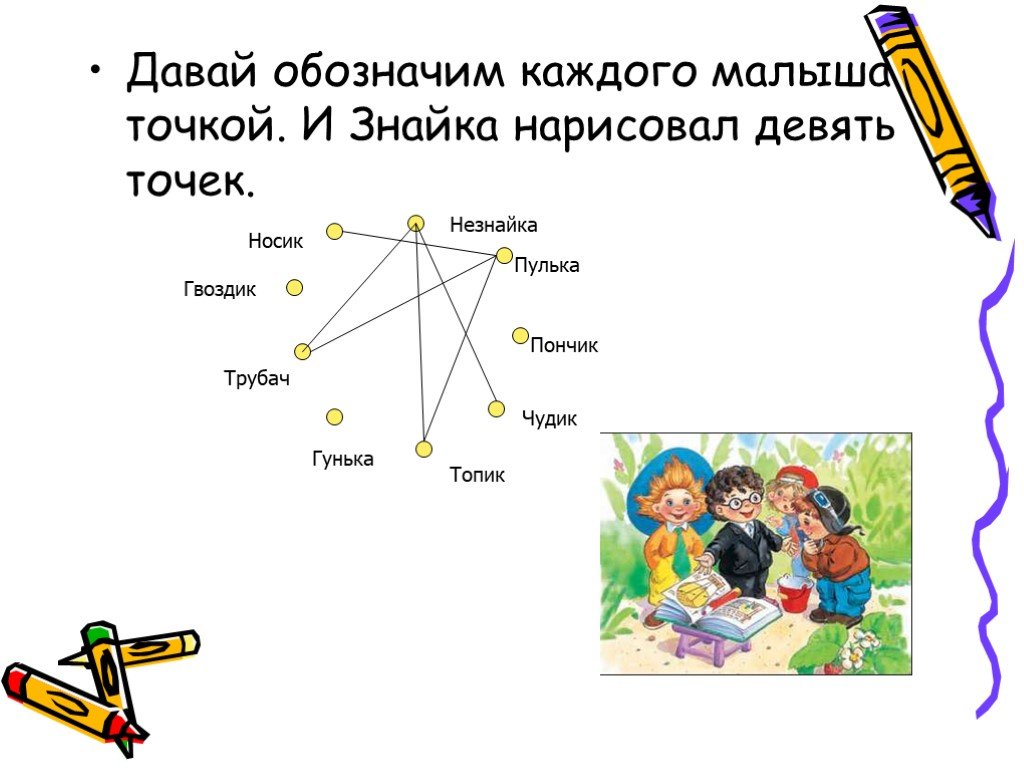


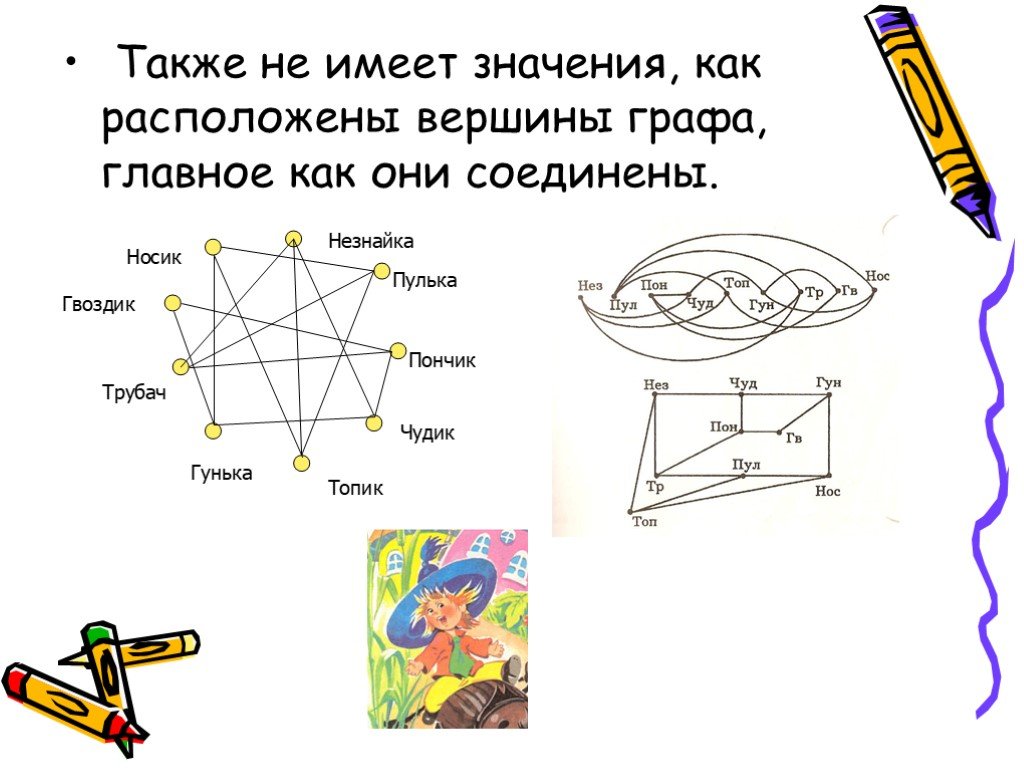







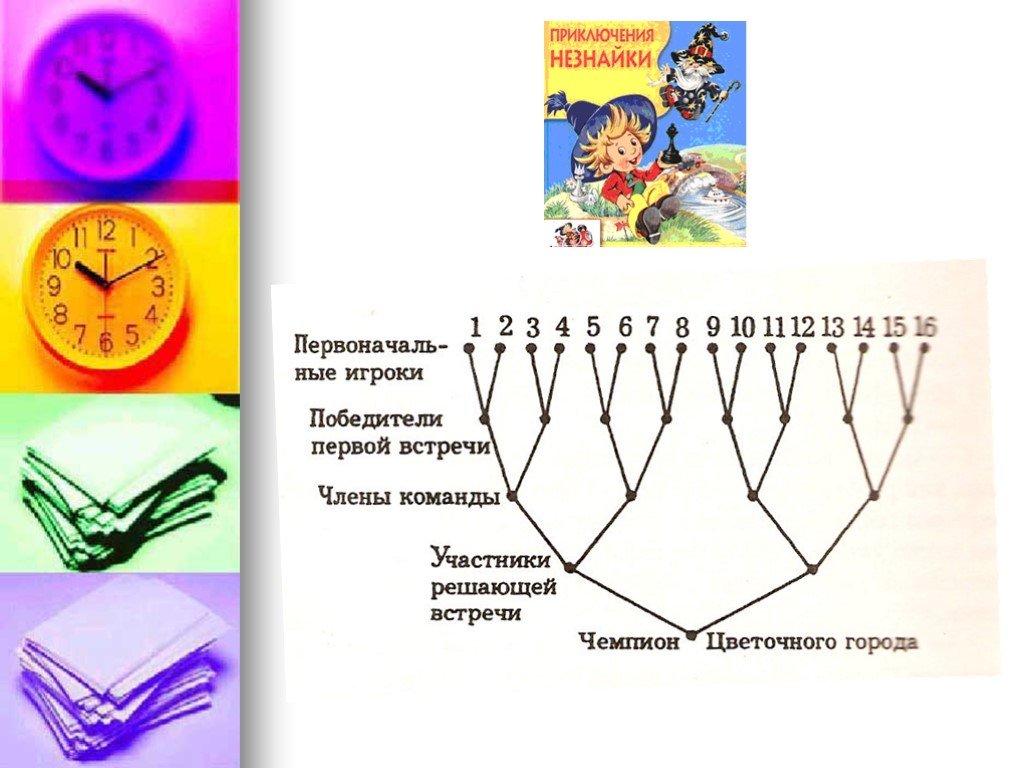









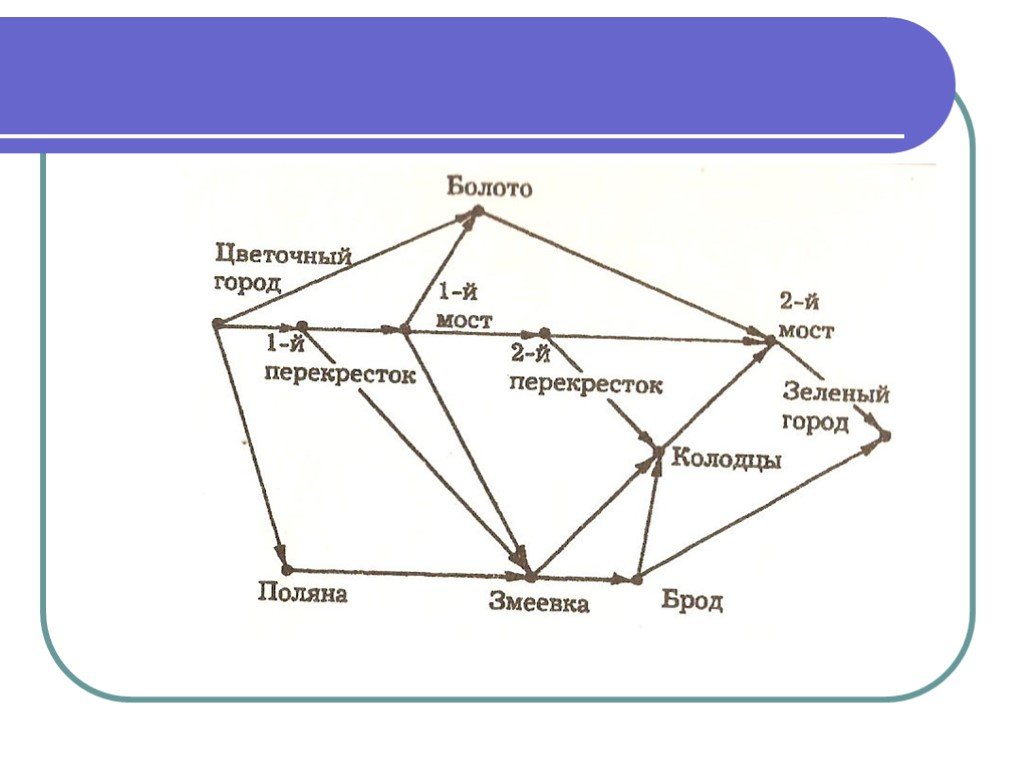















































![Автоматизация [Л] в конце слова Автоматизация [Л] в конце слова](/upload/resize_cache/webp/iblock/595/595d376379f9696b33d23ff72aff871b.webp)










