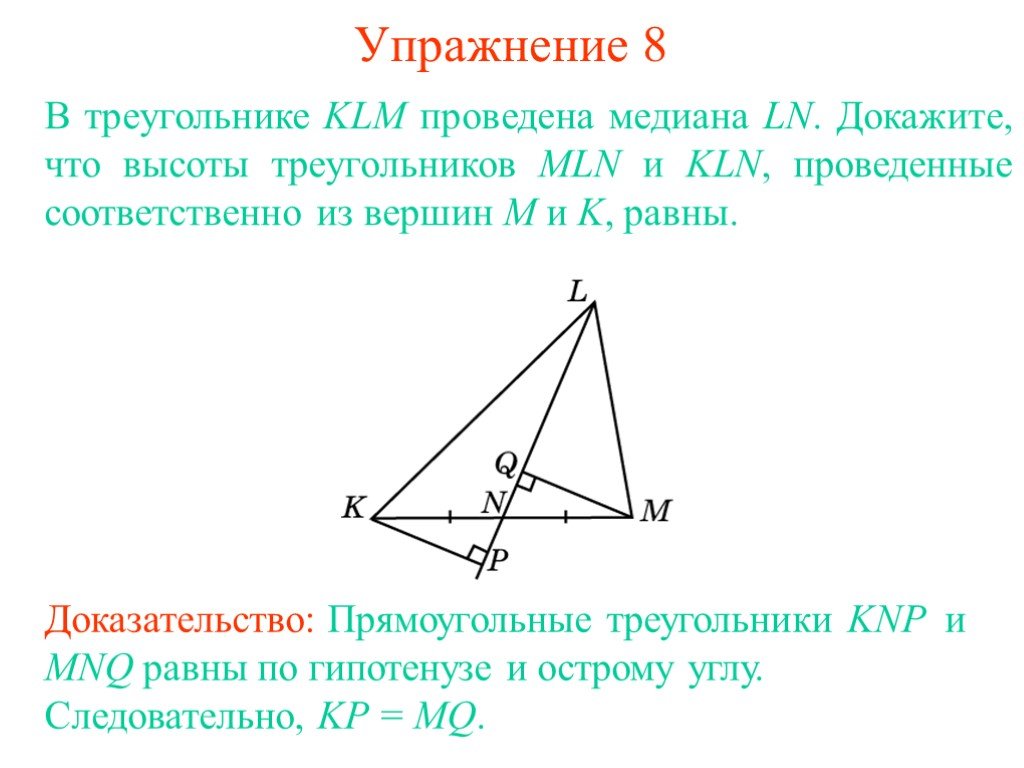
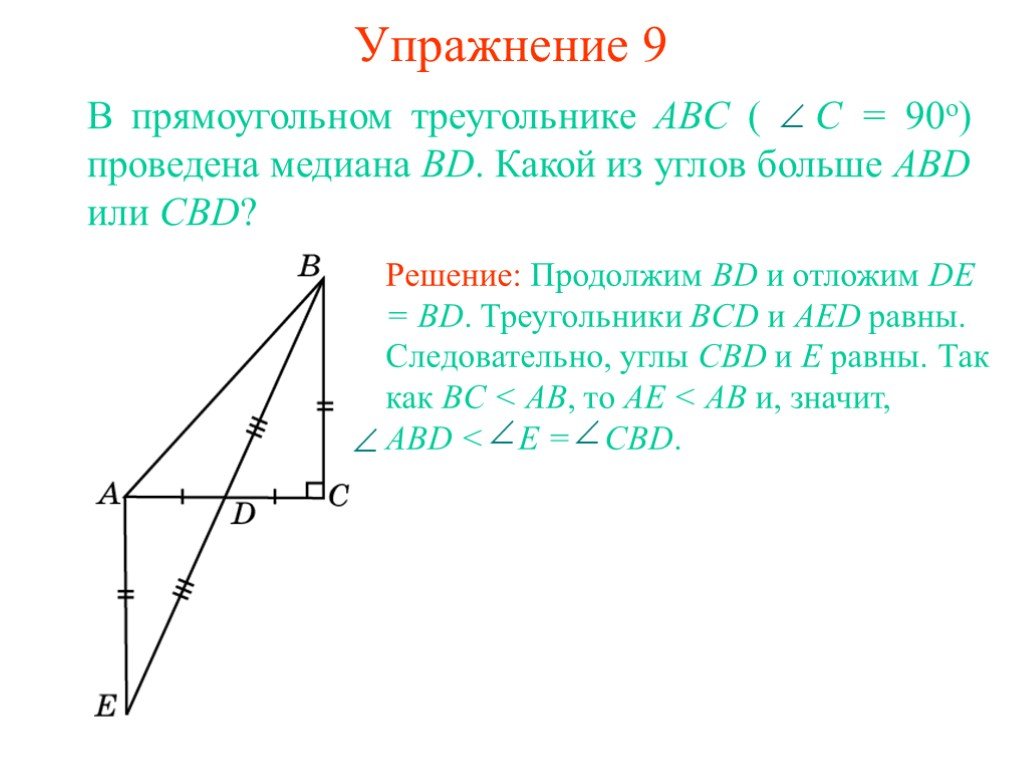
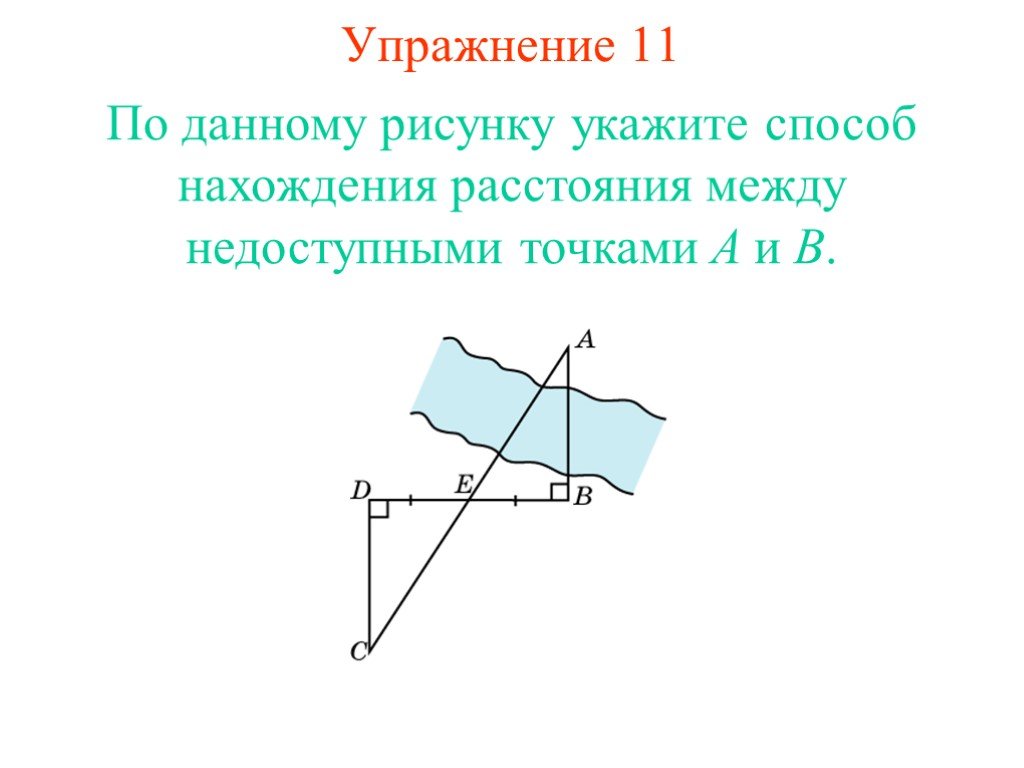
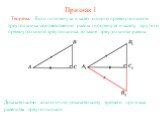
Презентация "Прямоугольные треугольники" по математике – проект, доклад

Прямоугольные треугольники

Треугольник называется прямоугольным, если …

у него есть прямой угол.

Гипотенузой называется сторона прямоугольного треугольника…

противолежащая прямому углу.

Остальные две стороны прямоугольного треугольника называются …

катетами.

Признак 1

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Теорема.

Признак 2

Теорема. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Доказательство: Пусть в прямоугольных треугольниках ABC и A1B1C1 равны гипотенузы AB и A1B1 и острые углы A и A1. Предположим, что AC и A1C1 не равны. На луче A1C1 от его начала A1 отложим отрезок AC.

Вопрос 1

Какой треугольник называется прямоугольным?

Ответ: Прямоугольным называется треугольник, у которого есть прямой угол.

Вопрос 2

Что называется гипотенузой прямоугольного треугольника?

Ответ: Гипотенузой называется сторона прямоугольного треугольника, противолежащая прямому углу.

Вопрос 3

Что называется катетами прямоугольного треугольника?

Ответ: Катетами называются стороны прямоугольного треугольника, противолежащие острым углам.

Упражнение 1

Что больше, катет или гипотенуза прямоугольного треугольника?

Ответ: Гипотенуза.

Упражнение 2

Может ли прямоугольный треугольник иметь стороны, равные 4, 5, 5?

Ответ: Нет.

Упражнение 3

Может ли прямоугольный треугольник иметь катеты 11 см и 111 см?

Ответ: Да.

Упражнение 4

Может ли прямоугольный треугольник иметь тупой угол?

Упражнение 5

Могут ли неравные прямоугольные треугольники иметь равные катеты?

Упражнение 6

Может ли прямоугольный треугольник быть: а) равнобедренным; б) равносторонним?

Ответ: а) Да, б) нет.

Упражнение 7

Стороны прямоугольного треугольника равны 3 см, 4 см, 5 см. Чему равна гипотенуза?

Ответ: 5 см.

Верно ли, что если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому другого прямоугольного треугольника, то такие треугольники равны.?

Докажите, что если две высоты треугольника равны, то этот треугольник – равнобедренный.

Упражнение 8

В треугольнике KLM проведена медиана LN. Докажите, что высоты треугольников MLN и KLN, проведенные соответственно из вершин M и K, равны.

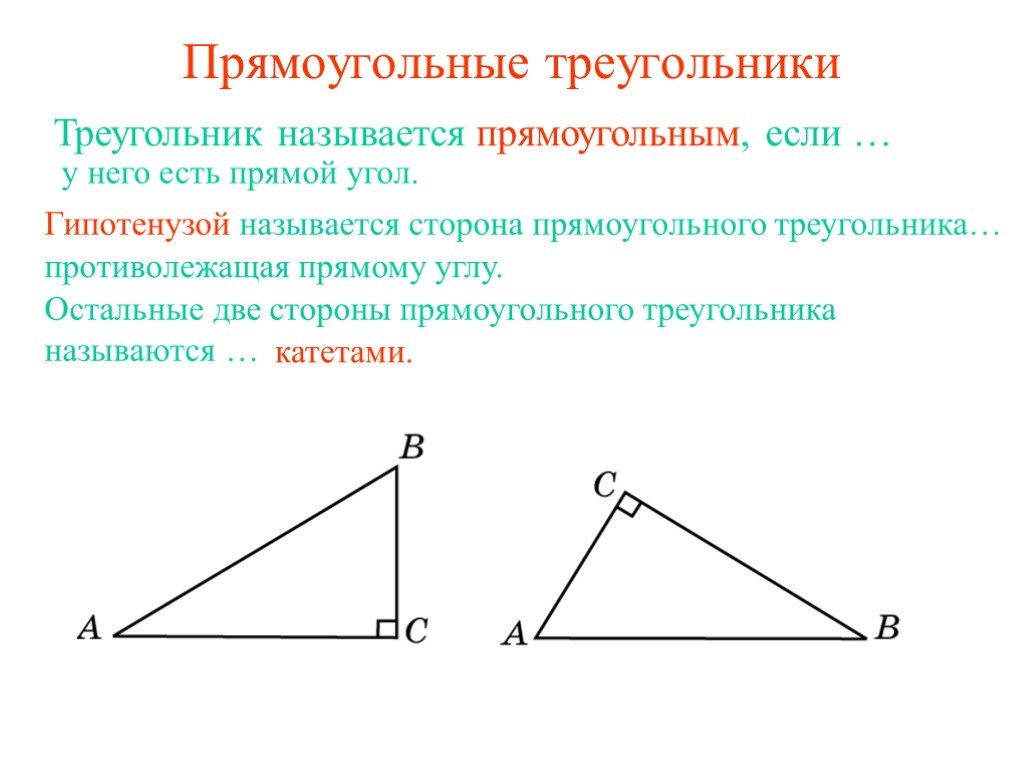
Доказательство: Прямоугольные треугольники KNP и MNQ равны по гипотенузе и острому углу. Следовательно, KP = MQ.

Упражнение 9

Упражнение 10

Упражнение 11

По данному рисунку укажите способ нахождения расстояния между недоступными точками A и B.