Презентация "Транспортная задача" по математике – проект, доклад
Презентацию на тему "Транспортная задача" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Транспортная задача (продолжение)
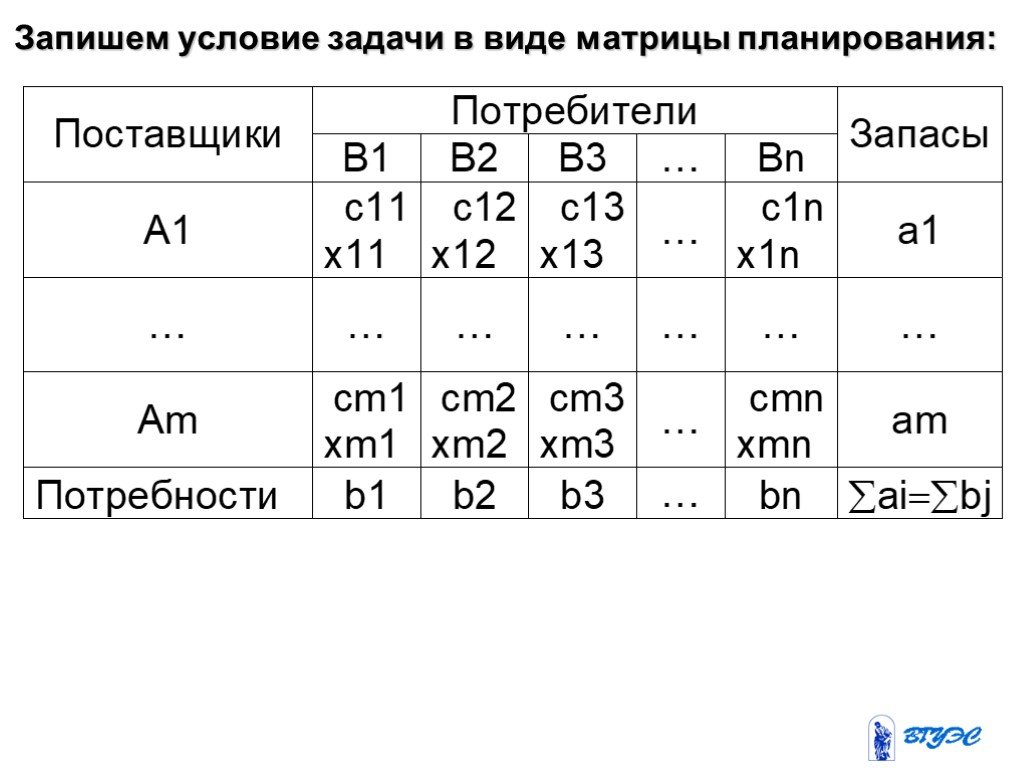
Метод Северо-западного угла. Метод минимальной стоимости (элемента). ПРИМЕР. В резерве трех железнодорожных станций A, B, C находятся соответственно ...Что такое задача
Я, Корпатыч, Крош, Лосяш. Догоняем дружно мяч. Нюша с Ёжиком пока - Запасных два игрока. А когда подучатся, Сколько нас получится? 7 ромашек наша ...Веселая математика - урок-игра
Веселая разминка. Упорядочение. Взаимно однозначное соответствие. Задачи о переправах. Задачи о переливаниях. Наш девиз:. Торопись! Ведь дни проходят! ...Веселая математика
08.02.2013. Ещё не решил, но буду стараться. Засели домики числами. Какое слово лишнее? УСЛОВИЕ ВОПРОС КВАДРАТ ответ. ЗАДАЧА. Раз, два, три, четыре, ...Весёлая математика
Привет! Я - Винни-Пух! К вам меня позвала Инна Евгеньевна, чтобы я проверил, чему вы научились ! Итак приступим…. 10, 35, 8, 67, 26. Познакомьтесь. ...Весёлая математика
Можете ли вы представить сухую, строгую математику занимательной и увлекательной? С трудом? При создании проекта мы поставили перед собой 3 цели: ...ЕГЭ математика готовимся к С4
Прямая, перпендикулярная гипотенузе, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок ...внеклассная математика
Испытание №1 Домик Лесовичка. «Посмотрите внимательно на мой домик и скажите, из чего он состоит». «Правильно! Мой домик Состоит из геометрических ...Арифметические действия над числами или зачем туристу математика?
27 сентября – день туриста. 34 х 2 = 90 : 30 = 9 + 45 = 11 х 3 = 80 – 19 = 55 : 5 = И У Р Т С 68 3 54 33 61 11. Что лежит в рюкзаке туриста? спички ...«Устный счёт» математика
1- 0,4 3 +2,4 3,2 – 2 3,2- 0,2 12,3 + 3,4 2,04 + 3,6 12 – 1,5 6,2- 2,6 ( 12,4 + 3,67)- 2,67 ( 45,06 + 23,5) – 40 ,06. 0,6 5,4 1,2 3 15,7 5,64 10,5 ...«Углы» математика
Цель урока:. познакомить учащихся с геометрической фигурой углом, с видами углов (прямой, тупой, острый), сформировать представления о существенных ...«Своя игра» математика
Математическая игра-викторина «Своя игра». Конец игры Литература. Задачи – шутки 50. Вопрос: Один господин написал о себе: «Пальцев у меня двадцать ...«Своя игра» математика
Условия игры:. Участники сами выбирают темы и вопросы. Вопрос выбирает правильно ответившая команда. 210 – 250 баллов – отметка «5». 110 -200 баллов ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Викторина "Ох уж эта математика"
Первый тур. Первый тур мы начинаем, Победителей узнаем. Здесь загадки и шарады. За разгадку – всем награды. Задание 1. 1.Шла старуха в Москву, и навстречу ...Викторина «О, счастливчик» (шуточные тесты математика вокруг нас)
ВОПРОС №1. 1 Какие числа используют при счете? А. Природные В. Естественные С.Натуральные Д. Порядковые. ВОПРОС №2. Какими бывают фотоаппараты? А. ...береза глазами математика
Цель. Целью данного исследования является выявление в повседневной жизни различных законов, которым нас обучают еще в школе. И как же все можно связать ...ГИА 2013. Модуль реальная математика №17
Модуль «РЕАЛЬНАЯ МАТЕМАТИКА» №17. Повторение (2). Найти расстояние от проектора С до экрана В. А В 180 см 90 см 240 см С H₁ H. Луч проектора АН₁⍊ ...Веселая математика
1. Разминка «Веселый урок». 2. Конкурс художников. Нарисуйте фигуры, не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии. 3. ...Конспекты
Что такое задача
Автор учебника:. И.И.Аргинская, Е.П.Бененсон, Л.С.Итина, С.Н.Кормишина. Тип урока:. . Урок «открытия» новых знаний. . Тема урока:. «Что такое ...Решение задача с различными величинами
Тема:. Решение задача с различными величинами. Цель:. Повторить соотношение всех изученных единиц (длины, массы, времени, объёма). Совершенствовать ...Конкретно-практическая задача по подбору предмета, равного данному по тяжести
Конспект урока математики в 1 классе. Разработала:. Губарева Ю.М.,. . учитель начальных классов. МОУ СОШ №125. г.Волгограда. Тема. ...Конкретно-практическая задача по подбору предмета, равного данному по тяжести
Конспект урока математики в 1 классе по учебнику. . Э.И. Александровой. Тема. : Конкретно-практическая задача по подбору предмета, равного данному ...Задачи в два действия – составная задача на нахождение суммы двух слагаемых
Тема:. Задачи в два действия – составная задача на нахождение суммы двух слагаемых. Цель:. Совершенствовать навыки сложения и вычитания с переходом ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 июня 2019
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию