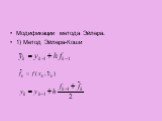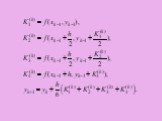Презентация "РЕШЕНИЕ ДИФУР" по математике – проект, доклад
Презентацию на тему "РЕШЕНИЕ ДИФУР" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Определение алгебраического уравнения. Кубические уравнения. Формула Кардано х= +. Пример:. Способы и методы решения уравнений. * Разложение на множители. ...РЕШЕНИЕ ЗАДАЧ ПО НАХОЖДЕНИЮ ВЕЛИЧИН ПО СУММЕ И РАЗНОСТИ
Многозначные числа. Читать, записывать и сравнивать многозначные числа; Учимся выполнять операции с числами: складывать, вычитать, умножать и делить ...РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КВАДРАТНЫХ И РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Математические фантазии на тему: «Ранетки». Задача №1 Найдите год создания группы «Ранетки», если цифра единиц на 5 больше цифры десятков, количество ...РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. 1) Если дно шляпы опустить на плоскость её полей, ...РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
Продолжите текст, соответствующий таблице. У старшего брата орехов было. в 5 раз меньше, чем у младшего. У младшего брата орехов было. в 5 раз больше, ...РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ
Урок в 5 «а» классе «Решение задач на движение». Основные понятия:.Скорость – V Время – t Расстояние – S. Формулы:.
пути S = V t скорости V = S ...
РЕШЕНИЕ АРИФМЕТИЧЕСКИХ ЗАДАЧ СОДЕРЖАЩИХ ЗАВИСИМОСТИ МЕЖДУ ВЕЛИЧИНАМИ
Тема урока:. Решение задач содержащих величины. Вместо точек вставьте нужные единицы измерения ( см, дм, м, кг, т…..) 4… = 400… 3…= 30… 20…= 2… 50…= ...Деление двузначного числа на однозначное РЕШЕНИЕ ЗАДАЧ
Р А З Г А Д А Й Т Е Р Е Б У С. НАЙДИТЕ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ. Н О С Л А Р К. РЕШИТЕ ЗАДАЧУ. Комната Малыша имеет длину 17 м, а ширину 4 м. Вычислите ...Задания по впр математика
№1. Найди значение примера: 43 − 27 Найди значение выражения: 7 + 3⋅(8 +12) ОТВЕТЫ 16 67. № 2. Рассмотри рисунок и ответь на вопрос: сколько рублей ...ЕГЭ математика готовимся к С4
Прямая, перпендикулярная гипотенузе, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок ...Конкурс "Ох, уж эта математика"
Зал красочно оформлен: на стенах математические газеты. Рисунки, кроссворды, высказывания ученых. Их портреты. В жюри трое родителей. Ведущая Счетный ...Занимательная математика для детей (устный счёт + учимся писать цифры)
По дороге мальчик и девочка шли, Оба по два рубля нашли. За ними ещё трое идут. Сколько они денег найдут? Повезло опять Егорке, У реки сидит не зря. ...Занимательная математика
Профессор ложится спать в 8 часов вечера и заводит будильник на 9 часов утра. Сколько часов будет спать профессор? Профессор. Рядом с берегом со спущенной ...Занимательная математика
РАЗМИНКА Миша тратит на дорогу в школу 5 минут. Сколько минут он потратит на эту дорогу вдвоём с мамой? Какие сто букв могут остановить движение транспорта? ...Занимательная математика
Интеллектуальная игра. Играем. Во сколько раз должны некие объекты превосходить остальные, чтобы по праву называться гигантскими? В миллиард раз (гига). ...Занимательная математика
Проблема проекта:. многим ученикам не интересно заниматься математикой. Они считают её сухой и незанимательной наукой, поэтому у них плохие отметки ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Занимательная математика
Подводная арифметика. Детёныш голубого кита выпивает за день 600 л молока. Сколько молока выпьет такой малыш за месяц (30 дней)? Ответ: 18 000 л. ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ...Конспекты
РЕШЕНИЕ ЗАДАЧ НА ОДНОВРЕМЕННОЕ ДВИЖЕНИЕ В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ
5. . ТЕМА: «РЕШЕНИЕ ЗАДАЧ НА ОДНОВРЕМЕННОЕ ДВИЖЕНИЕ. . В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ». Цель:. . Закрепить умение решать задачи на различные ...РЕШЕНИЕ ЗАДАЧ И УРАВНЕНИЙ
Урок математики во 2 классе разработала учитель начальных классов МОУ СОШ№1 города Карталы Казанцева Татьяна Сергеевна. Тема. : Решение задач и уравнений. ...РЕШЕНИЕ ЗАДАЧ НА ВЫЧИТАНИЕ
Урок по математике. «. РЕШЕНИЕ ЗАДАЧ НА ВЫЧИТАНИЕ. ». Урок – закрепление. 1 класс. Разработала: Пузина Н.В. . . г. ...РЕШЕНИЕ ЗАДАЧ
УРОК МАТЕМАТИКИ. ТЕМА: РЕШЕНИЕ ЗАДАЧ. ЦЕЛЬ: Познакомить учащихся с решением задач нового вида. ЗАДАЧИ: Развивать и закреплять навыки счета с ...ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ
МКОУ СОШ п.В.Фиагдон. Конспект урока по математике во 2 классе. . . ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ. . . . . Учитель начальных классов ...ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА НА ОДНОЗНАЧНОЕ. РЕШЕНИЕ ЗАДАЧ
УРОК МАТЕМАТИКИ В 3 КЛАССЕ. Учитель: Малышева Ирина Серафимовна, город Озёрск Челябинской области. Тема. :. «ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА НА ОДНОЗНАЧНОЕ. ...ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
МБОУ Дорогобужская СОШ №2. Современный урок математики (по курсу « Алгебра» 8 класс). ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ. (Урок ...ВЗАИМОСВЯЗЬ МЕЖДУ ВЕЛИЧИНАМИ СКОРОСТЬ, ВРЕМЯ, РАССТОЯНИЕ, РЕШЕНИЕ ЗАДАЧ
ПРЕДМЕТ: МАТЕМАТИКА. КЛАСС: 3. ТЕМА УРОКА: «ВЗАИМОСВЯЗЬ МЕЖДУ ВЕЛИЧИНАМИ СКОРОСТЬ, ВРЕМЯ, РАССТОЯНИЕ, РЕШЕНИЕ ЗАДАЧ». ТИП УРОКА: закрепление знаний, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 июня 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию