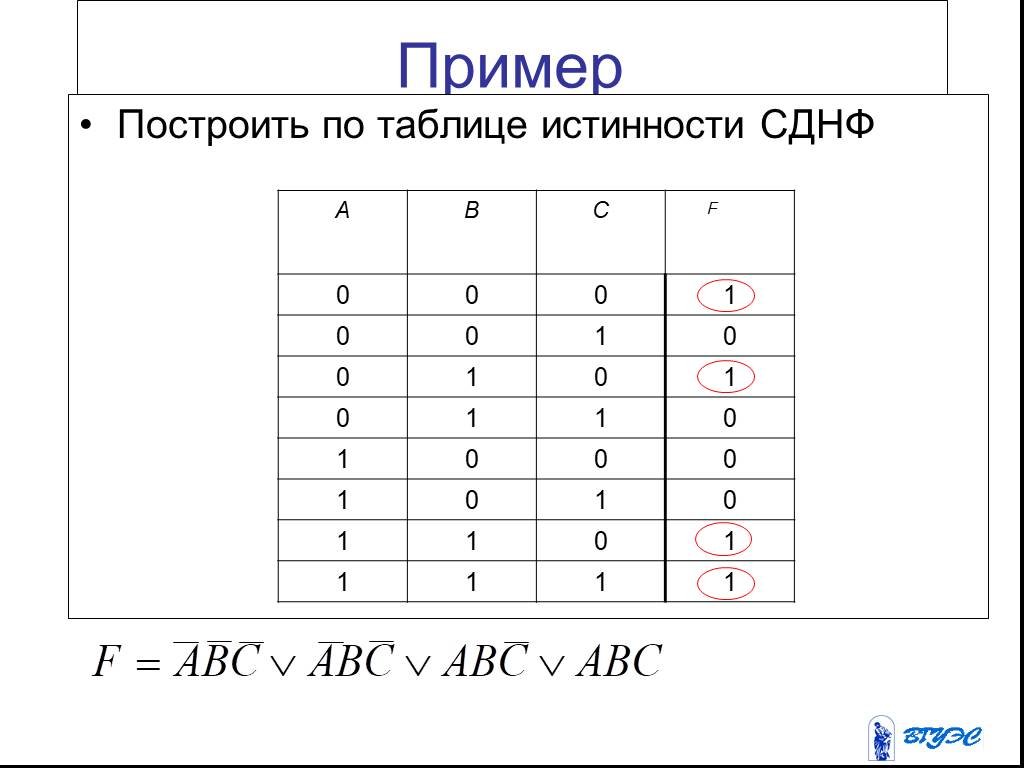
Презентация "Дизъюнктивные нормальные формы (ДНФ). Совершенные дизъюнктивные нормальные формы (СДНФ)" по математике – проект, доклад

Кафедра математики и моделирования Старшие преподаватели Е.Д. Емцева и Е.Г. Гусев Курс «Высшая математика» Лекция 3. Тема: ДНФ. СДНФ.

Цель: Определить ДНФ, СДНФ, сформировать навык приведения высказывания к ДНФ, СДНФ.

Определение 1

Конъюнкция логических переменных или их отрицаний называется элементарной конъюнкцией.

Пример Определение 2

Высказывание называется дизъюнктивной нормальной формой (ДНФ), если оно представляет собою дизъюнкцию элементарных конъюнкций.

Общий вид ДНФ:

3. Дизъюнктивные нормальные формы (ДНФ)

Примеры

Теорема

Любое высказывание приводимо к ДНФ.

Схема приведения высказывания к ДНФ

Избавиться от импликации и эквивалентности, используя законы 16), 17) 2) Донести отрицания до переменных, используя законы Моргана. 3) Раскрыть скобки, используя дистрибутивные законы. 4) Упростить полученное высказывание.

Привести высказывание к ДНФ

5.Построение высказываний по таблице истинности. Совершенные дизъюнктивные нормальные формы (СДНФ)

Определение 1 Пусть – некоторое множество логических переменных. Элементарная конъюнкция, в которую входят все логические переменные, называется полной элементарной конъюнкцией относительно множества X .

Определение 2 Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие ее элементарные конъюнкции являются полными. Примеры

СДНФ

Приведение высказывания к СДНФ

Теорема Высказывание, не являющееся тождественно ложным, приводимо к СДНФ. Правило приведения высказывания к СДНФ СДНФ содержит столько полных элементарных конъюнкций, сколько единиц в последнем столбце таблице истинности. Вид каждой полной элементарной определяется соответствующим набором значений переменных, а именно, если переменная принимает значение 0, то над ней в полной элементарной конъюнкцией ставится отрицание, иначе – отрицание не ставится.

Построить по таблице истинности СДНФ

Задача

«Вернувшись домой, Мегрэ позвонил на набережную Орфевр. - Говорит Мегрэ. Есть новости? - Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. Затем звонила … - Все. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.» Что знал Мегрэ?

Решение задачи

Пусть P=« Франсуа был пьян» L=«Франсуа лжет» I=«Этьен убийца» U=«Убийство произошло после полуночи» Тогда получим высказывание

Так как , то Этьен - убийца

Вопросы: Является ли СДНФ-ДНФ? Можно ли построить СДНФ для высказывания, в таблице истинности которого отсутствуют 1?