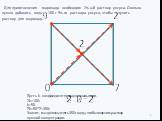
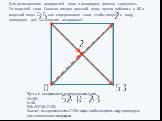
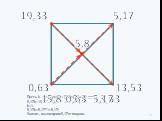
Презентация "Квадрат Пирсона" по математике – проект, доклад
Презентацию на тему "Квадрат Пирсона" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
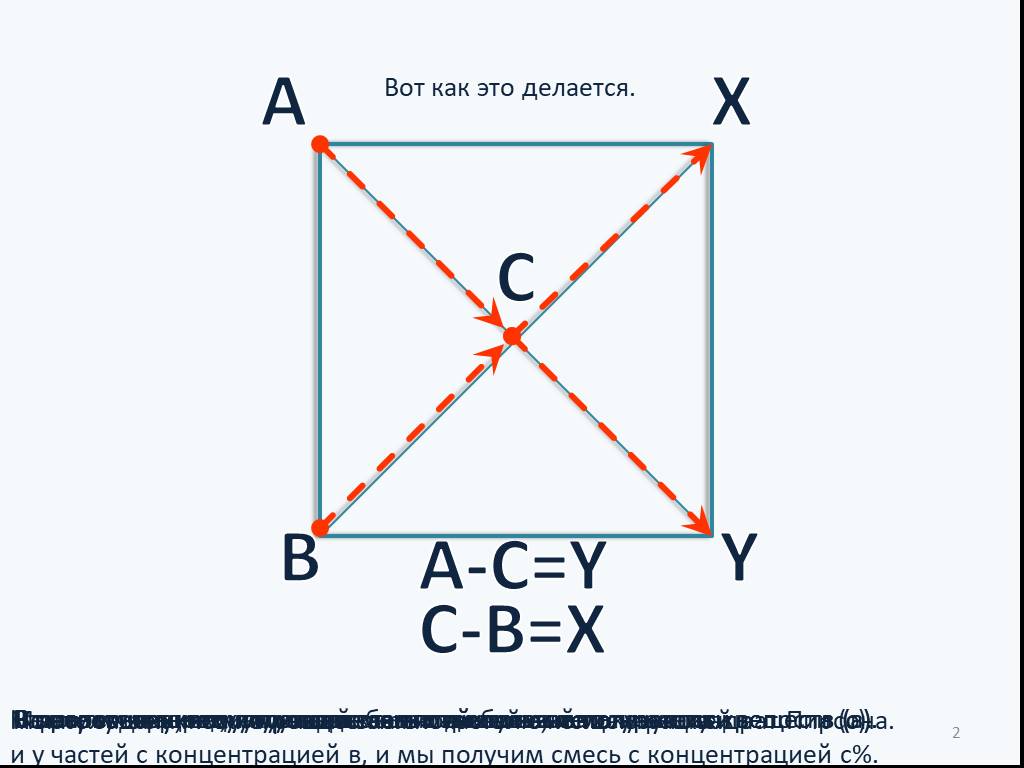
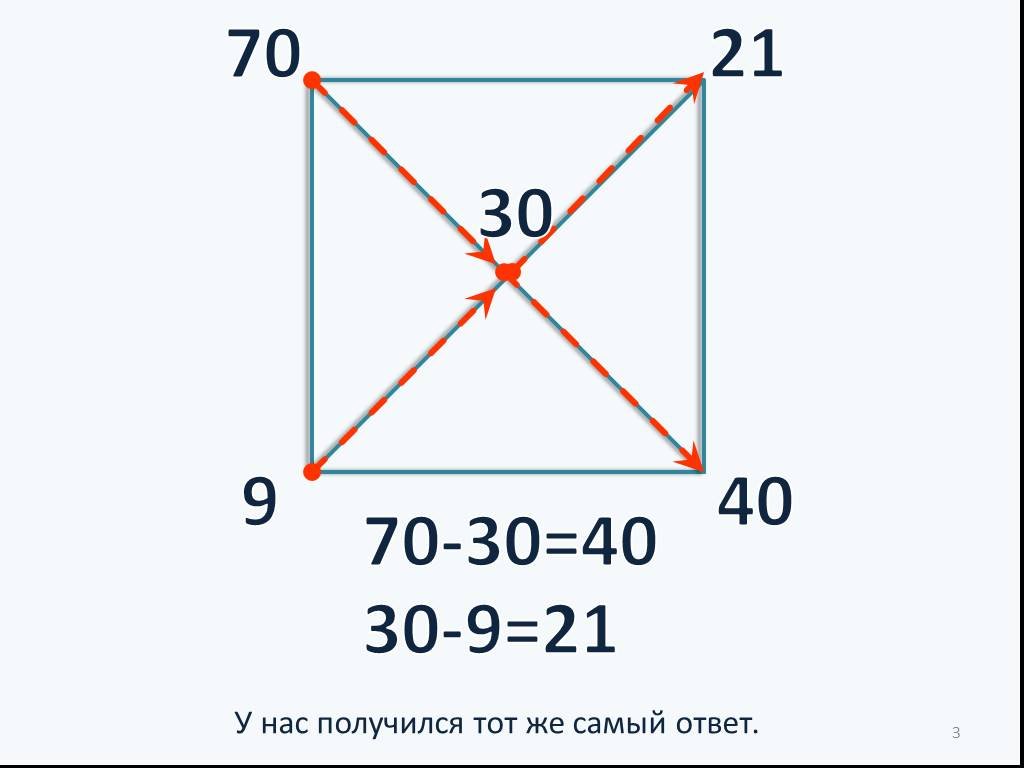
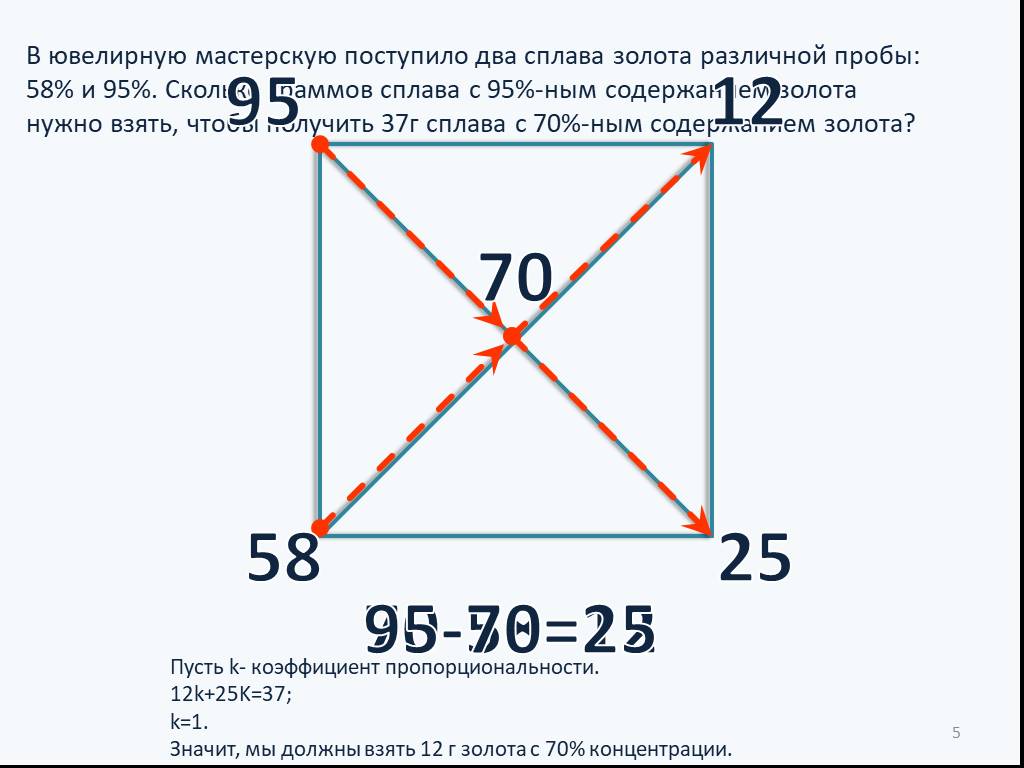
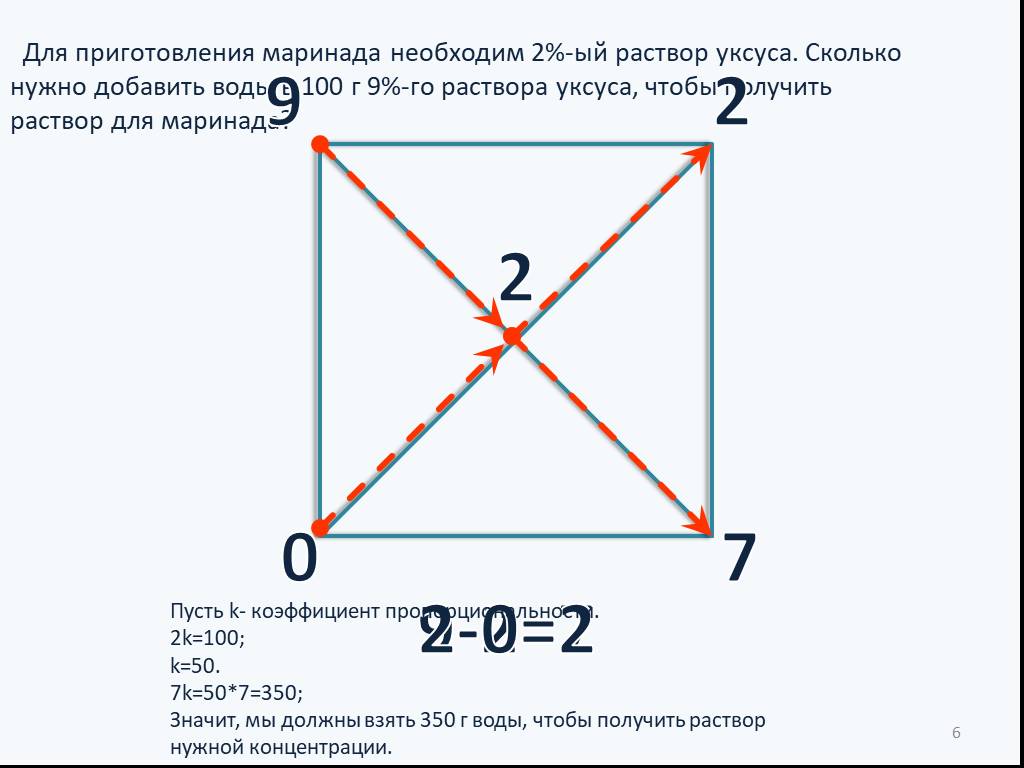
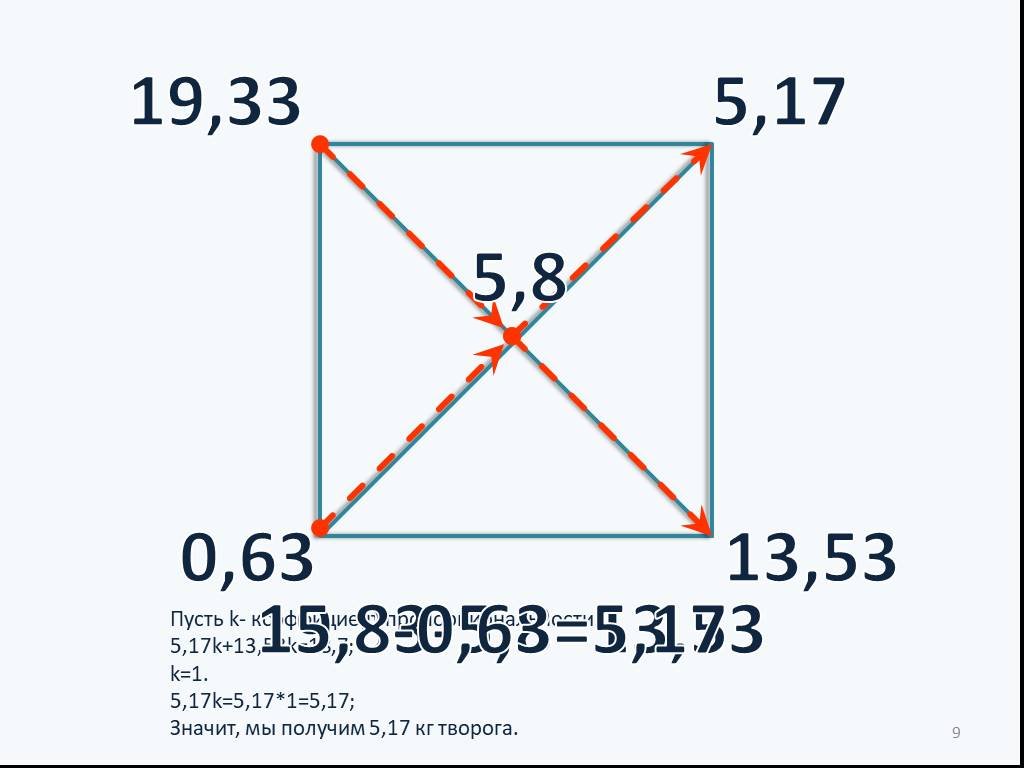
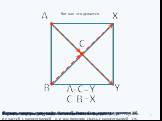
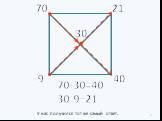
Слайды презентации
Список похожих презентаций
Квадрат суммы и квадрат разности
. . . . . . . . . . . . . . . . . ...Квадрат и прямоугольник
Цели проекта:. сформировать умение работать с информацией, находить источники, из которых ее можно почерпнуть; сформировать умения проводить исследования, ...Квадрат Полибия
В Древней Греции (II в. до н.э.) был известен шифр, который создавался с помощью квадрата Полибия. Шифр, созданный с помощью квадрата Полибия – шифр ...Прямоугольник. Квадрат
Прямоугольник. Квадрат. Периметр. Площадь. Прямоугольник –. четырехугольник, у которого все углы прямые. Прямоугольник. Чертеж. Формулы. Р = 2( а ...Квадрат
Распределите геометрические фигуры на группы. . . . . 9 + 9 + 9 + 9 = 36 (см) Р = ? Начертить квадрат со стороной 9 см. Найти его периметр. 9 см. ...Квадрат суммы, квадрат разности
Прочитай выражения. Продолжи формулу и прочитай её. Продолжим. Раскройте скобки. В классе: №817( в, д), 819(а, б), 821(а, б) Дом. задание: 817(а, ...Квадрат суммы. Квадрат разности
Прочитай выражения. Продолжи формулу и прочитай её. Продолжим. Раскройте скобки. В классе: №817( в, д), 819(а, б), 821(а, б) Дом. задание: 817(а, ...Квадрат в жизни
(Автор неизвестен). Пришёл из школы старший брат, Из спичек выложил квадрат. Дала мне мама шоколад, Я дольку отломил - квадрат. И стол -квадрат, и ...Квадрат и куб
10 +15 - 10 +13 - 16 6 3 :15 75 7 14 30 5. Задача: В кинотеатре на дневной сеанс продали 210 билетов, на утренний сеанс – на 60 билетов меньше, чем ...Квадрат
Цель:. - закрепить определения ромба, квадрата, прямоугольника и их свойства; - учить доказывать соответствующие теоремы и применять их при решении ...Квадрат
Жила на свете важная фигура. Важность ее признавалась всеми людьми, так как при изготовлении многих вещей форма ее служила образцом. Кого бы ни встретила ...Квадрат
Цели: ознакомить детей с геометрической фигурой – квадрат, научить чертить его на клетчатой бумаге, ознакомить со свойствами квадрата; развивать логическое ...Квадрат
Тема: «Квадрат». Сегодня на уроке Я узнаю… Я научусь… Я смогу…. План:. Узнаем, какой прямоугольник называют квадратом. Познакомимся со свойствами ...Квадрат
История появления магических квадратов. Любознательность - один из всегдашних верных признаков энергичного ума. Джонсон, Сэмюэль. Магический квадрат ...Квадрат суммы и квадрат разности
По какому признаку можно провести классификацию данных выражений на 2 группы? I )(7-b)(7+b) II) (x+y)(x+y) III) (4-a)(4-a) IV ) (c-6)(c-6) V) (m-x)(m-x) ...Квадрат и куб числа
Прочитайте выражения. 3 * 3 5 * 5 6 * 6. Эти выражения в буквенной форме имеют вид n * n. Произведение n * n называют квадратом n числа и обозначают ...Квадрат суммы и квадрат разности двух выражений
Игра «Третий лишний». 3² 9 6 4а² 16а² (4а)² (а + b)² (a + b)(a + b) a² + b² (c – d)² (c – d)(c + d) (c – d)(c – d) (7 – 3)² 16 40 (– a)² a² – a² (a ...Квадрат и куб числа
-ввести определение квадрата числа; -ввести определение куба числа; -ввести на их примерах понятие степени числа; -научиться применять правила на ...Квадрат суммы. Квадрат разности
Тема урока:. Квадрат суммы. Квадрат разности. Цель урока:. Познакомиться с формулами квадрата суммы и квадрата разности и их применением для разложения ...Квадрат и куб числа
Проверка домашнего задания. №632 . Напишите выражение по схеме:. 1387 64. Угадайте корни уравнения:. х ∙ х = 25 у ∙ у = 81 а ∙ а = 1 b∙ b ∙b = 0. ...Конспекты
Квадрат и куб числа
Использование презентации как печатной основы урока на уроке математики. в 5 классе по теме «Квадрат и куб числа». Ход урока. Сообщение цели ...Геометрические фигуры. Квадрат
Урок математики по ФГОС. Автор: Федяева Татьяна Николаевна. МКОУ «Барятинская сош». . Урок по математике. Математика, 2 класс, УМК «Школа ...Квадрат и куб числа
Урок по теме "Квадрат и куб числа", 5-й класс. Замалетдинова Алсу Мансуровна. учитель математики, МБОУ «Убеевская средняя школа. . Дрожжановского ...Квадрат суммы и квадрат разности
Муниципальное казенное общеобразовательное учреждение. лицей №11 г.Россошь Россошанского района. Воронежской области. . . Открытый урок ...Квадрат суммы. Квадрат разности
Тема урока: "Квадрат суммы и квадрат разности". 7-й класс. . Нуждина Алёна Владимировна, учитель математики. . . Цели урока:. . Формирование ...Квадрат и куб числа
Мудла Елена Петровна. ,. учитель математики,. . МБОУ «Гимназия №1» г. Ноябрьска ЯНАО. Разработка урока по теме «Квадрат и куб числа», 5 класс. ...Квадрат суммы двух выражений
МАТЕМАТИКА 7 класс. . Квадрат суммы двух выражений. . Цели и задачи. . Образовательные. – познакомить учащихся с формулой сокращенного умножения ...Квадрат
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №26 с углубленным изучением отдельных предметов» г. Нижнекамска ...Квадрат
Составитель:. Учитель начальных классов. ГБСКОУ школы №3 Красногвардейского района. Лосева И.М._________________. Конспект урока математики. ...Квадрат
Открытый урок во 2 классе по математике. Тема: Квадрат. Цели:. . ознакомить детей с геометрической фигурой – квадрат, научить чертить его на клетчатой ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:31 марта 2019
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию