Презентация "Первообразная" (11 класс) по математике – проект, доклад
Презентацию на тему "Первообразная" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Первообразная и интеграл
Исторические сведения. Интегральное исчисление возникло из потребности создать общий метод Разыскания площадей , объемов и центров тяжести. В зародышевой ...Первообразная и неопределенный интеграл
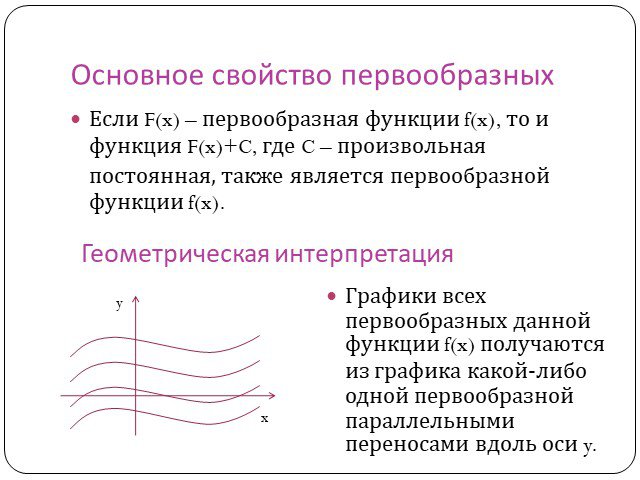
По заданным производным найдите исходные функции. дифференцирование. интегрирование. Обозначения: ПЕРВООБРАЗНАЯ. Функция F называется первообразной ...Первообразная
Содержание. Открытие первообразной Понятие первообразной Основное свойство первообразной Три правила нахождения первообразной Интегралы Неопределенный ...Конспекты
Первообразная и интеграл
Автор: Макарова Татьяна Павловна, учитель математики ГБОУ СОШ №618 г. Москвы. . Тест. Первообразная и интеграл. Автор:. . . Макарова Татьяна ...Первообразная и интеграл
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа №3 г. Козьмодемьянска». . Республики Марий Эл. . ...Первообразная
Урок математики в 11 классе по теме «Первообразная». Цель: сформировать понятие о первообразной, дать ее определение, сформулировать правила нахождения ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Классы:
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию






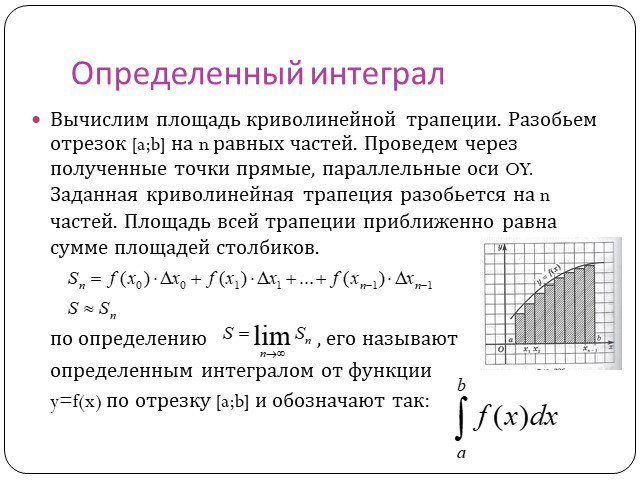















![Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые, параллельные оси OY. Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков. по определению , его называют опр Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые, параллельные оси OY. Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков. по определению , его называют опр](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen7.jpg)


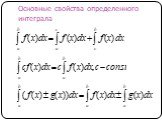
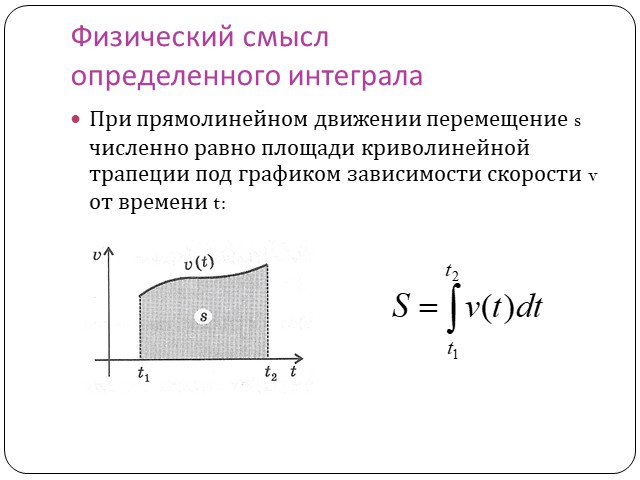
![Геометрический смысл определенного интеграла. Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Геометрический смысл определенного интеграла. Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen11.jpg)
![Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen12.jpg)
![Замечание: Если функция изменяет знак на промежутке [a;b] , то Замечание: Если функция изменяет знак на промежутке [a;b] , то](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen13.jpg)


![Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций: Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen16.jpg)
![Объем тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]: Объем тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:](https://prezentacii.org/upload/cloud/15/01/11212/images/thumbs/screen17.jpg)













