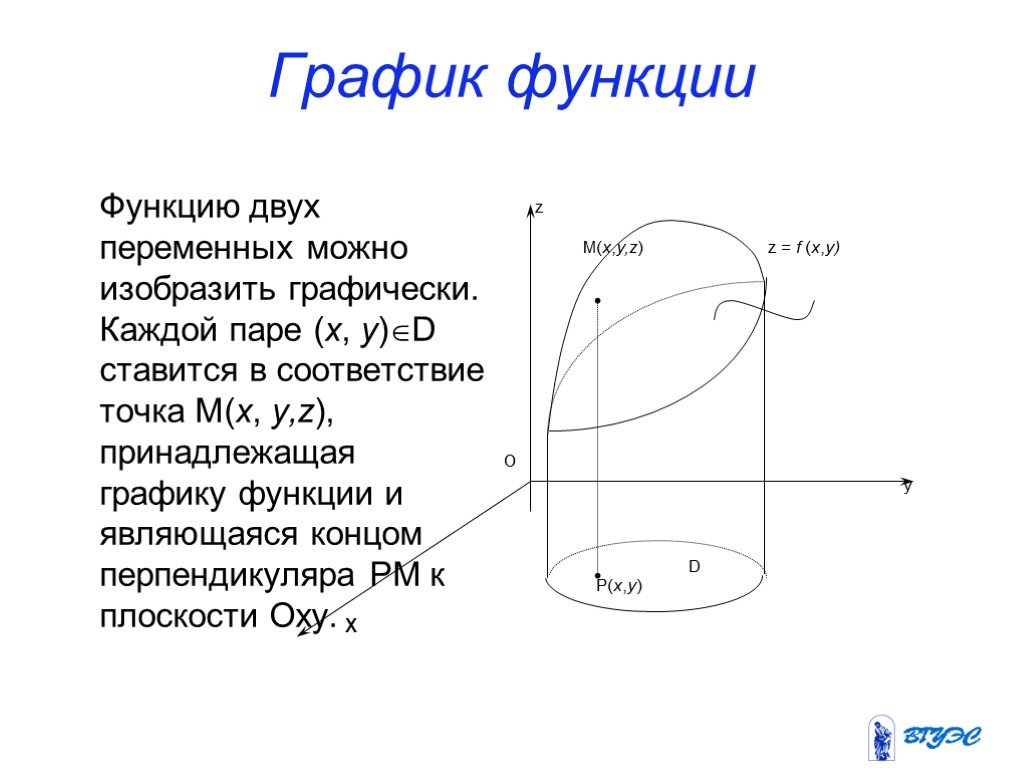
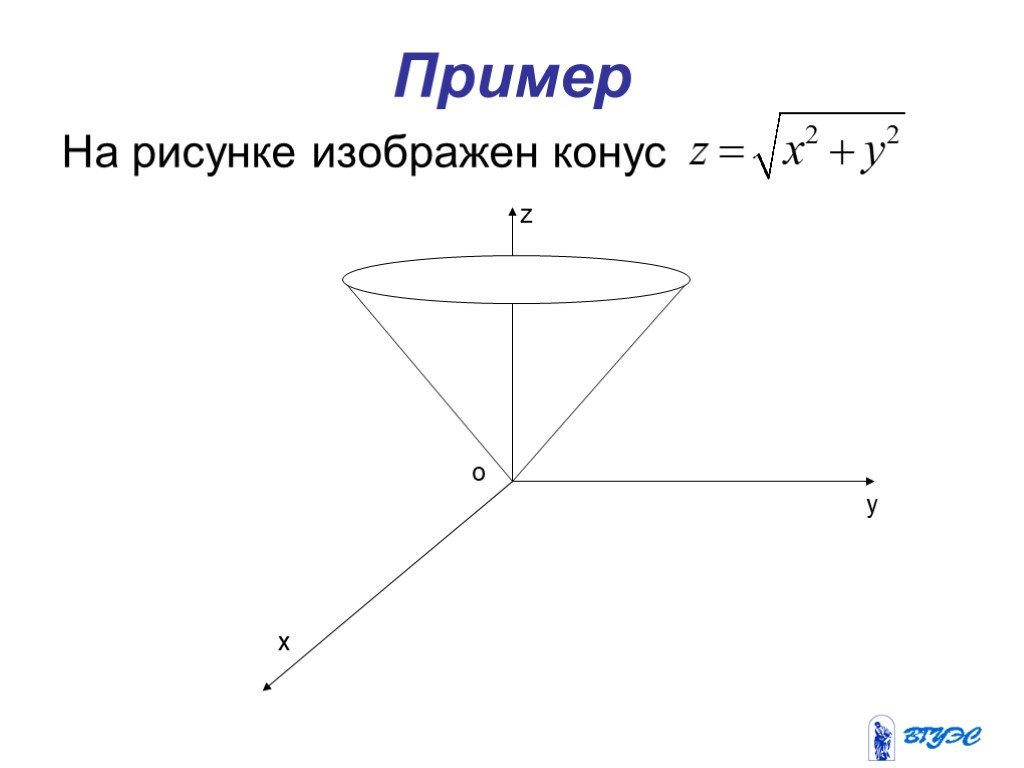
Презентация "Функции нескольких переменных" по математике – проект, доклад

Математический анализ

Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования

Литература

Основная литература: Л. Д. Кудрявцев. Курс математического анализа, т. 1, 2 Г. Н. Берман. Сборник задач по курсу математического анализа. Н. С. Пискунов. Дифференциальное и интегральное исчисления, т. 1, 2.

Дополнительная литература: Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. 1, 2.

Учебно-методические разработки: Л. Я. Дубинина, Л. С. Никулина, И. В. Пивоварова. Курс лекций по высшей математике, ч. 1, 2.-Владивосток, изд. ВГУЭС, 2001. Сборник задач по высшей математике. Сост. И. В. Пивоварова, Л. Я. Дубинина, Л. С. Никулина. -Владивосток, изд. ВГУЭС, 2002.

Содержание

Функции нескольких переменных Дифференциальные уравнения 1-го, 2-го и более высокого порядков Кратные интегралы Числовые ряды Степенные ряды Ряды Фурье

Функции нескольких переменных

Лекция 1

Определение функции двух переменных

Определение. Если каждой паре (x,y) значений двух независимых друг от друга переменных величин x и y из некоторого множества D соответствует единственное значение величины z, а каждому z соответствует хотя бы одна пара (x,y), то мы говорим, что z есть функция двух независимых переменных x и y, определенная в D.

Обозначения

При этом пишут: Если паре соответствует число , то пишут Или называется частным значением функции при

График функции 2-х переменных

Геометрическое место точек, координаты которых удовлетворяют уравнению z= =f(x,y), называется графиком функции двух переменных.

График функции

Функцию двух переменных можно изобразить графически. Каждой паре (x, y)D ставится в соответствие точка M(x, y,z), принадлежащая графику функции и являющаяся концом перпендикуляра PM к плоскости Oxy.

х

Пример

На рисунке изображен конус

x y z o

Предел функции 2-х переменных

-окрестностью точки называется совокупность всех точек, лежащих внутри круга радиуса с центром в точке .

Таким образом, -окрестностью точки является множество точек, УДОВЛЕТВОРЯЮЩИХ НЕРАВЕНСТВУ

о у

Определение предела функции 2-х переменных

Число А называется пределом функции z=f(x,y) при , если для любого числа найдется такая -окрестность точки ,что для всех точек М(х,у), лежащих в этой окрестности , выполняется условие При этом пишут: или

Функция нескольких переменных называется бесконечно малой, если ее предел равен нулю. Правила предельного перехода, установленные для функции одной переменной, остаются справедливыми.

Непрерывность

Функция z=f(x,y) называется непрерывной в точке , если выполнены условия: 1)функция определена в точке , 2)если существует , 3)если

Другое определение: Функция z=f(x,y) называется непрерывной в точке , если в этой точке бесконечно малому приращению аргументов соответствует бесконечно малое приращение функции, т. е. где .

Области

Областью (открытой областью) называется множество точек плоскости, обладающее свойствами: каждая точка области принадлежит ей вместе с некоторой окрестностью (свойство открытости); всякие две точки области можно соединить непрерывной линией, целиком лежащей в этой области (свойство связности).

Точка называется граничной точкой области G, если любая окрестность этой точки содержит как точки области G, так и точки, ей не принадлежащие. Множество всех граничных точек области называется ее границей. Если к открытой области присоединить ее границу, то полученное множество точек называется замкнутой областью.

Область называется ограниченной, если можно подобрать круг, полностью ее покрывающий. В противном случае область называется неограниченной

Функция называется непрерывной в области G, если она непрерывна в каждой точке этой области.

Свойства функции, непрерывной в замкнутой области

Если функция непрерывна в ограниченной замкнутой области, то она в этой области 1)ограничена: ; 2) принимает наименьшее и наибольшее значения (соответственно m и M); 3) принимает хотя бы в одной точке области любое численное значение, заключенное между m и M.

Частные приращения функции 2-х переменных

Разность = f (x+x, y) – f (x, y) называется частным приращением функции f (x, y) по переменной x. Разность = f (x, y+y) – f (x, y) называется частным приращением функции f (x, y) по переменной y.

Частные производные

Определение. Если существует = , то он называется частной производной (первого порядка) функции z = f (x, y) по переменной x и обозначается

Аналогично определяется частная производная по переменной y: = Эту производную обозначают

Заметив, что вычисляется при неизменном y, а – при неизменном x, можно сделать вывод: правила вычисления частных производных совпадают с правилами дифференцирования функций одной переменной, но при вычислении полагают , а при вычислении полагают .

Производные высших порядков

Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции. Например, для функции 2-х переменных имеем:

Равенство смешанных производных

Теорема. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности. Так, ,