Слайд 2179
Точечные и пространственные данные
Два вида данных: Точечные (координатные) данные: Объекты (в бд) – кортежи из k элементов в k-мерном пространстве. Геометрически, элементы кортежа соответствуют координатам в пространстве. Домены для элементов могут быть произвольными. Применение: многоатрибутное извлечение из реляционных бд, текстовые базы данных, векторы характеристик для мультимедийных объектов (см. темы 6 и 10 данного курса) Пространственные данные: Объекты обладают определенной формой и размером. Например, линии, прямоугольники, многоугольники на двухмерной поверхности, или линии, параллелепипеды, многогранники в трехмерном пространстве. Точки – частный случай пространственных данных. Применение: САПР-чертежи, проектирование интегральных схем, географические бд, обработка изображений (см. тему 9)

Слайд 3180
Методы доступа к многомерным данным: Доступ к точечным данным (PAM – Point Access Method) Доступ к пространственным данным (SAM – Spatial Access Method) Общие требования к структурам многомерных данных: Простые операции требуют небольшого числа доступов к диску Высокий коэффициент использования памяти (около 70% достаточно) Простые алгоритмы для поиска и обновления Отсутствие ‘предпочтительных’ измерений Кластеризация объектов должна соответствовать геометрической близости (необходимо для эффективной обработки пространственных запросов) Динамическая реорганизация – адаптация структуры к увеличению или уменьшению количества данных (наподобие B-деревьев) Поддержка различных типов запросов

Слайд 4181 Точечные данные
Свойства точечного пространства: Фиксированное число (k) измерений, у каждого измерения свой собственный домен значений Объекты с переменной размерностью (такие как документы с ключевыми словами) могут быть преобразованы в образы фиксированной длины (сигнатуру, битовую матрицу, ...) Разбиение пространства с точечными данными: Разбиение, задаваемое данными (data-driven) (например, k-d-дерево, см. далее) Разбиение, задаваемое пространством (space-driven) (например, сеточная организация, см. далее)

Слайд 5182
Виды запросов: Запросы по точному совпадению (exact-match queries): все координаты (атрибуты) зафиксированы в запросе; временная сложность - O(log n) Запросы по частичному совпадению (partial-match queries): в запросе указываются t из k координат, остальные координаты могут принимать произвольные значения; нижняя граница для сложности в наихудшем случае – O(n1-t/k) Пространственные запросы (range queries): для каждого измерения указан диапазон значений; в случае точного совпадения – диапазон [c,c]; в случае частичного – (-,) для незаданной координаты Запросы по наилучшему совпадению (best-match queries): найти ближайших соседей для точки/области, заданной в запросе

Слайд 6183
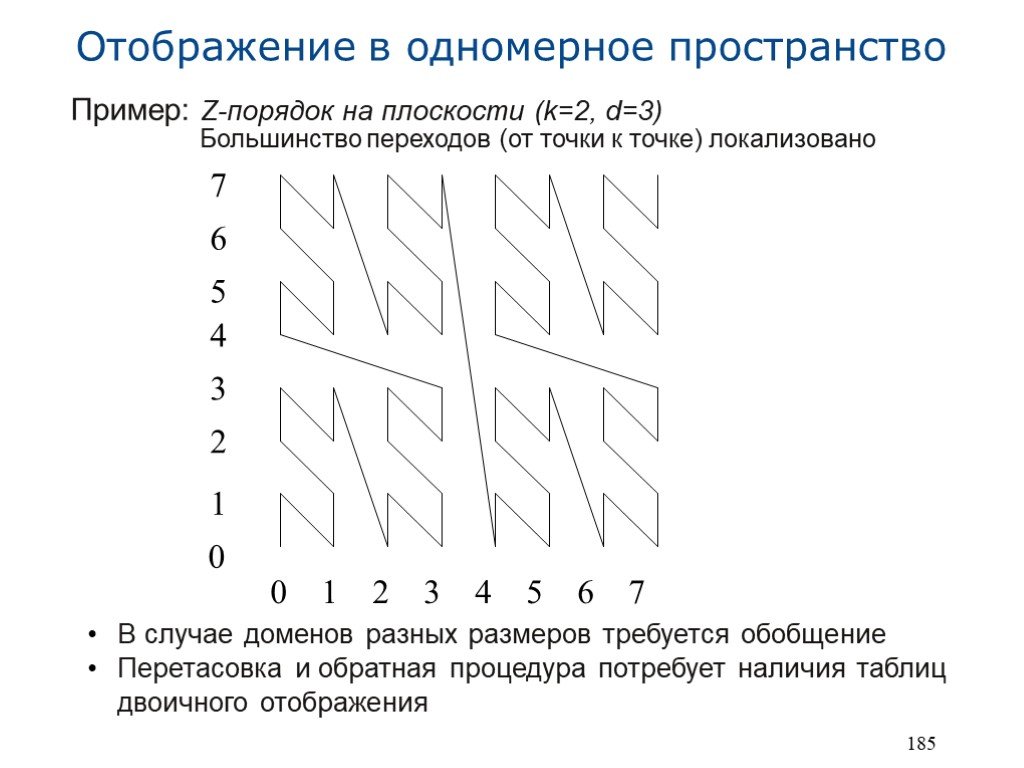
Отображение в одномерное пространство
Зачем отображать в одномерное пространство? Одномерное пр-во проще и для него есть эффективные структуры данных – например, B-деревья (которые требуют линейного пр-ва для хранения данных и логарифмического времени для основных операций). Первая идея (осуществления отображения): связать координатные значения в цепочку и, далее по получившимся значениям построить одномерный индекс на основе B+-дерева Недостаток: такое отображение будет корректным только для самых ‘левых’ измерений, но не для остальных Кривые, заполняющие пространство (space filling curves): отображения n-мерного пространства в одномерное; расстояния в целом не сохраняются, но точки, расположенные вблизи в многомерном пр-ве, с высокой вероятностью остаются вблизи и в одномерном пр-ве Полностью покрывают всю пространство Кривая не пересекается сама с собой (проходит через каждую точку только один раз) Соседние точки в многомерном пр-ве с большой вероятностью соседи на кривой

Слайд 7184
Более симметричное решение: перетасовать двоичные представления координат. Пусть: k – размерность пространства диапазон координатных значений: 0..2d-1 рассмотрим произвольную точку: P = , или в двоичном виде: , ,...,Pk-1,0,Pk-1,1,...,Pk-1,d-1>> ‘перетасованное’ двоичное представление: shuffle(P) = Получаем Z-порядок1 - кривую, заполняющую пространство Если p и q точки в k-мерном пространстве, то p Z q тогда и только тогда, когда shuffle(p) shuffle(q) Структура данных: B+-дерево, хранящее ‘перетасованные’ представления точек 1 Z-order, другое название - порядок Мортона
Слайд 8Пример: Z-порядок на плоскости (k=2, d=3) Большинство переходов (от точки к точке) локализовано
В случае доменов разных размеров требуется обобщение Перетасовка и обратная процедура потребует наличия таблиц двоичного отображения

Слайд 9186
Операции с данными в Z-порядке: Поиск по точному совпадению, вставка, удаление и модификация осуществляются просто, с помощью соответствующих операций с B+-деревом Больше усилий требуется для пространственных запросов: Генерация k-мерных регионов поиска (search region, далее SR или S-регион) путем повторяющегося разбиения пространства Множество точек, удовлетворяющих запросу – регион запроса (query region, далее QR) Задача: найти покрытие QR одним или несколькими S-регионами QR и SR – k-мерные (гипер-)прямоугольники В ходе разбиения, новый SR может находиться в трех позициях относительно QR: SR – вне QR; SR не содержит точек, удовлетворяющих запросу. Далее его можно не учитывать. SR – внутри QR; все точки SR удовлетворяют запросу. Соответствующие записи извлекаются, производится процедура обратная перетасовке (из одномерного в k-мерное), и возвращаются как результат запроса. SR и QR перекрываются; SR разбивается на два меньших S-региона, которые затем рекурсивно рассматриваются.

Слайд 10187
Замечания: Проверка расположения SR и QR относительно друг друга не требует доступа к данным (обращений к диску) Для эффективности стараемся иметь дело с регионами, образующими непрерывную подпоследовательность Z-порядка Правило разбиения: На i-ом уровне рекурсии, разбить SR на две равные части вдоль измерения i mod k Обозначения: нижний:верхний пределы для k размерностей: Разбиение SR пополам вдоль i-ого измерения дает два следующих S-региона: SRleft = left(SR, i) = SRright = right(SR, i) =
Слайд 11188
Алгоритм: RangeSearch(QR, SR, level) --- В начале SR – всё k-мерное пространство, level = 0 if SRQR=0 then ничего не делать else if SRQR then SRlo := of SR -- нижний левый угол SRhi := of SR -- правый верхний угол прочитать запись t, где key shuffle(SRlo) while t shuffle(SRhi) do вернуть unshuffle(t) прочитать следующую запись t -- согласно Z-порядку else RangeSearch(QR, left(SR, level mod k), level+1) RangeSearch(QR, right(SR, level mod k), level+1) end
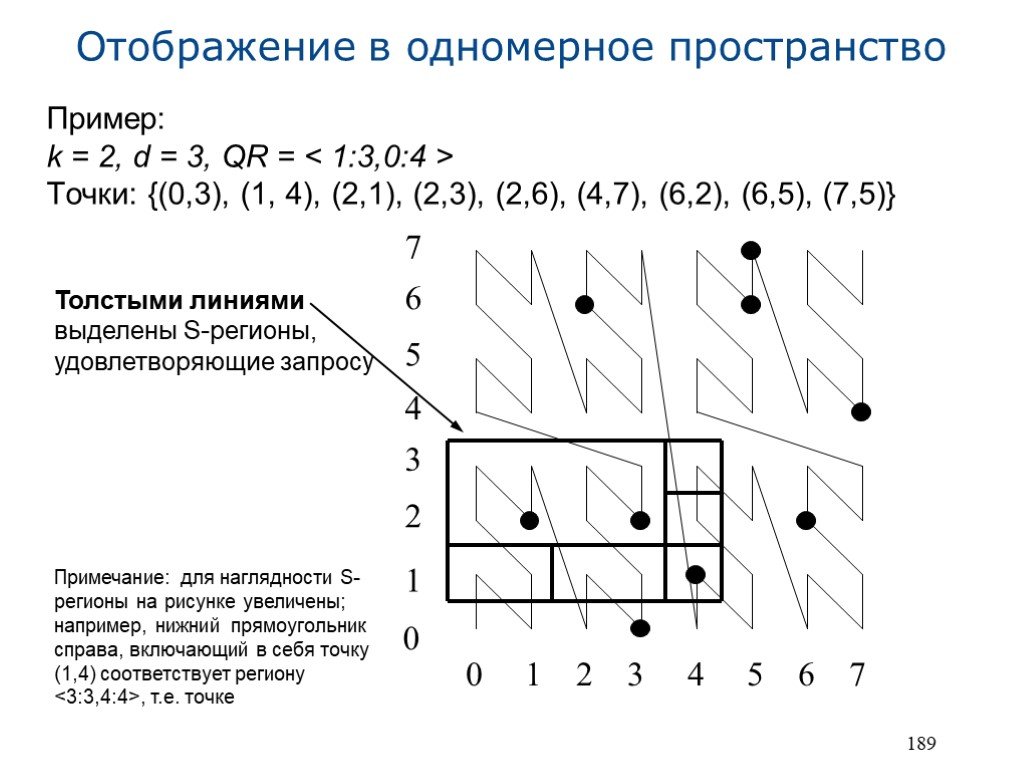
Слайд 12189
Пример: k = 2, d = 3, QR = Точки: {(0,3), (1, 4), (2,1), (2,3), (2,6), (4,7), (6,2), (6,5), (7,5)}
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
Толстыми линиями выделены S-регионы, удовлетворяющие запросу Примечание: для наглядности S-регионы на рисунке увеличены; например, нижний прямоугольник справа, включающий в себя точку (1,4) соответствует региону , т.е. точке
Слайд 13190
Процесс нахождения S-регионов, удовлетворяющих пространственному запросу (пример работы алгоритма RangeSearch):
(вне) (внутри) (вне) (вне) (вне) (внутри) (вне) (внутри) (вне) (внутри) (вне) (внутри) (вне) (внутри) (вне)
Слайд 14191
Несколько замечаний о пространственных запросах: Точки внутри каждого SR расположены в Z-порядке и значит могут быть последовательно извлечены, начиная с крайнего левого угла региона В районе границы с QR создается много S-регионов, что может привести к увеличению числа доступов к диску Стек рекурсии для алгоритма RangeSearch может быть сжат до размера двойной длины записи (представляющей точку) в битах, т.к. по заданному SR можно определить S-регионы более высоких уровней Модификация алгоритма: найти надмножество регионов, покрывающих QR, остановившись на уровне разбиения, который обеспечит неизбыточный доступ к диску Обобщение: Универсальное B-дерево (UB-tree) [3]: может использоваться для пространственных объектов

Слайд 15192
Сеточная1 организация
В отличии от предыдущей структуры: явно задаваемое разбиение пространства Свойства: Динамичность: гибкие вставка и удаление; локальная реорганизация Настраиваемость: адаптация структуры к распределению точечных данных Симметричность: относительно всех измерений Сбалансированность: время выполнения удовлетворительно для любых операций Основные принципы: Эффективное хранение динамического множества точек в многомерном пространстве Поиск по точному совпадению потребует (около) два обращения к диску Поддержка пространственных запросов; кластеризация соседних точек Разбиение пространства не зависит от точечных данных Общие черты с: Расширяемым хешированием (которое можно назвать сеточной организацией для одномерного пространства) Системой близнецов (адреса и размеры блоков не произвольны) 1 - grid

Слайд 16193
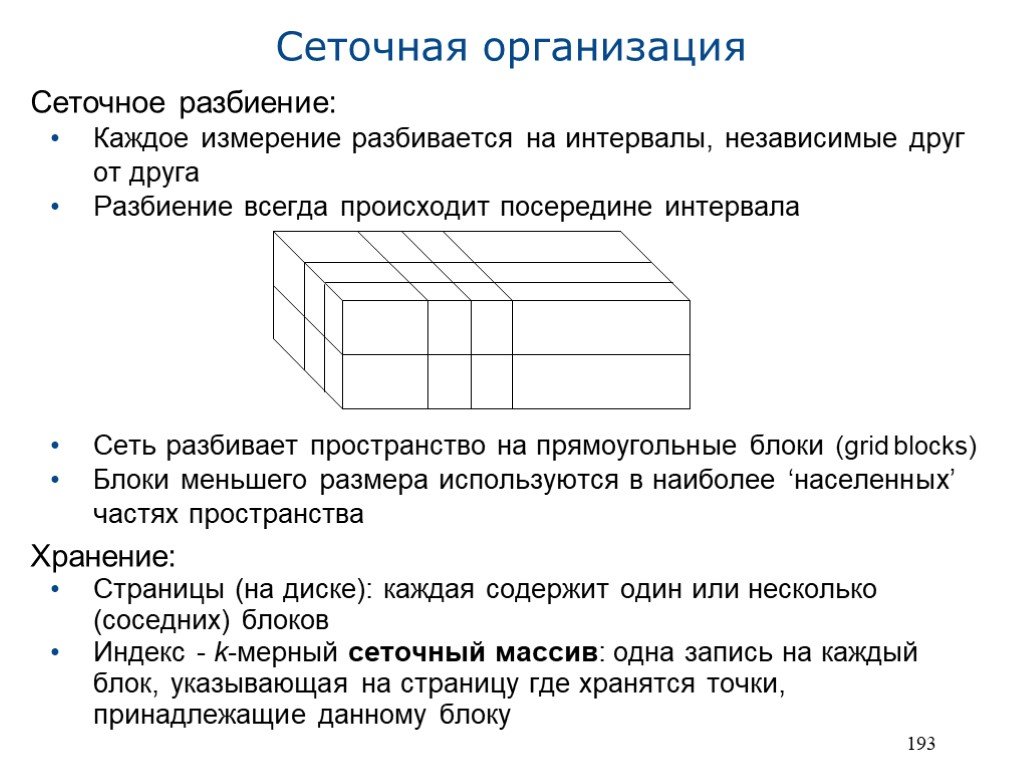
Сеточная организация
Сеточное разбиение: Каждое измерение разбивается на интервалы, независимые друг от друга Разбиение всегда происходит посередине интервала Сеть разбивает пространство на прямоугольные блоки (grid blocks) Блоки меньшего размера используются в наиболее ‘населенных’ частях пространства Хранение: Страницы (на диске): каждая содержит один или несколько (соседних) блоков Индекс - k-мерный сеточный массив: одна запись на каждый блок, указывающая на страницу где хранятся точки, принадлежащие данному блоку

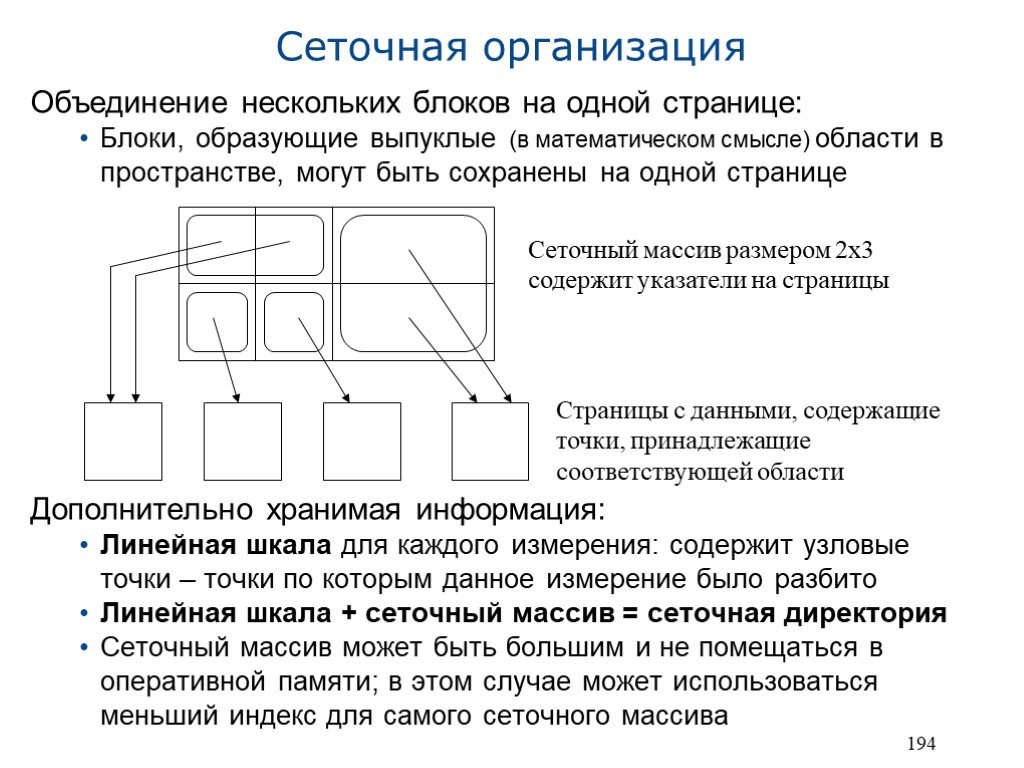
Слайд 17194
Объединение нескольких блоков на одной странице: Блоки, образующие выпуклые (в математическом смысле) области в пространстве, могут быть сохранены на одной странице Дополнительно хранимая информация: Линейная шкала для каждого измерения: содержит узловые точки – точки по которым данное измерение было разбито Линейная шкала + сеточный массив = сеточная директория Сеточный массив может быть большим и не помещаться в оперативной памяти; в этом случае может использоваться меньший индекс для самого сеточного массива
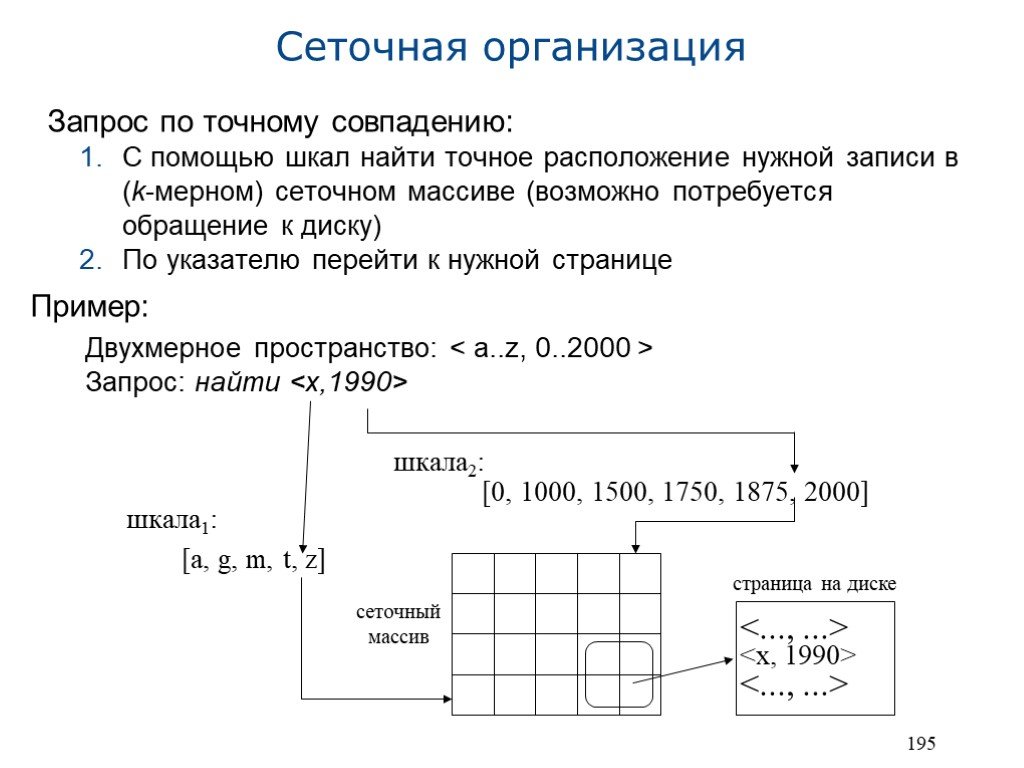
Слайд 18195
Запрос по точному совпадению: С помощью шкал найти точное расположение нужной записи в (k-мерном) сеточном массиве (возможно потребуется обращение к диску) По указателю перейти к нужной странице Пример: Двухмерное пространство: Запрос: найти
[0, 1000, 1500, 1750, 1875, 2000]
[a, g, m, t, z] <... ...> сеточный массив шкала1: шкала2: страница на диске
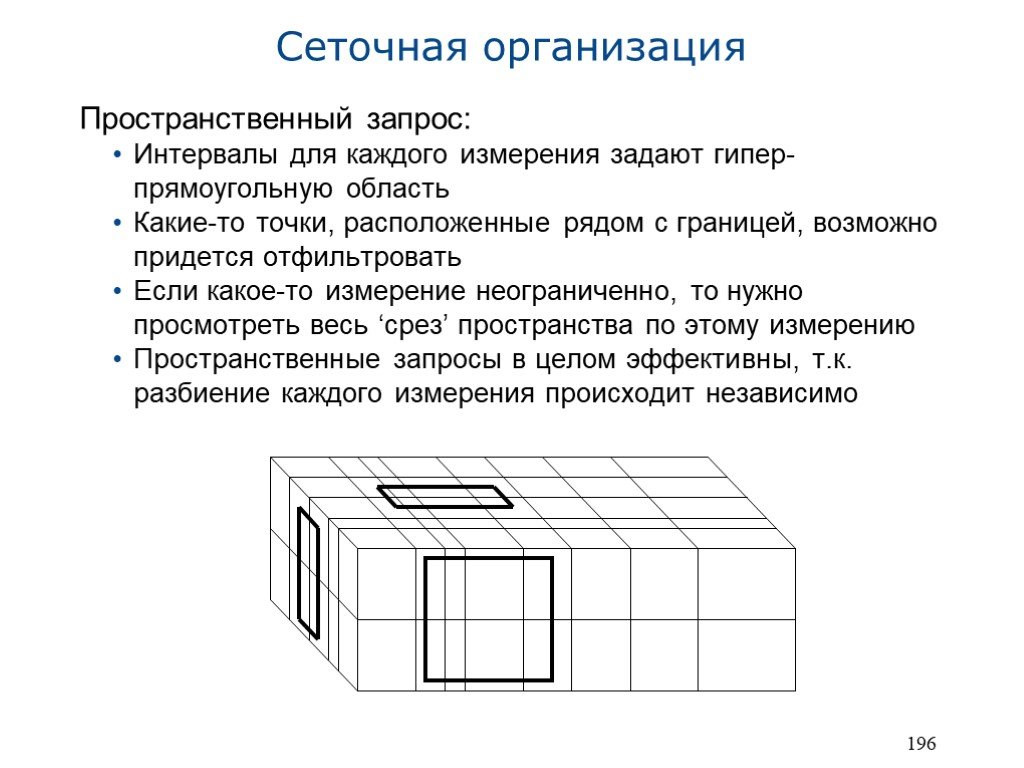
Слайд 19Пространственный запрос: Интервалы для каждого измерения задают гипер-прямоугольную область Какие-то точки, расположенные рядом с границей, возможно придется отфильтровать Если какое-то измерение неограниченно, то нужно просмотреть весь ‘срез’ пространства по этому измерению Пространственные запросы в целом эффективны, т.к. разбиение каждого измерения происходит независимо

Слайд 20197
Операция вставки: Найти нужную страницу (как в запросе по точному совпадению) Далее возможны три альтернативы: Страница вмещает в себя новую точку Страница переполняется, при этом страница описывает область в пространстве, состоящую из более чем одного блока: Разбить область на две выпуклые области по существующей узловой точке (на линейной шкале одного из измерений) Распределить точки между двумя страницами (для каждой из образованных областей) и внести изменения в сеточный массив При разбиении (также как и при слиянии) должно выполняться правило близнецов (деление пополам) Например, разбиение можно произвести по средней узловой точке, относящейся к тому измерению, что имеет наибольшее количество узловых точек в этой области Повторить разбиение в том случае, если все точки оказались в одной половине

Слайд 21198
Операция вставки (продолжение): Страница переполняется, при этом страница описывает только один блок: Пространство должно быть разбито Выбрать измерение по которому будет производиться разбиение (например, в порядке очередности) Точка разбиения – средняя точка интервала в котором произошло переполнение Внести изменения в сеточную директорию: реплицировать элементы (относящиеся к расщепленному интервалу) сеточного массива и обновить соответствующую линейную шкалу На этом шаге получаем ситуацию b), которая возможно потребует еще одного разбиения и т.д., до тех пор пока хотя бы одна точка не окажется в разных с другими точками блоках Эмпирические наблюдения: В стационарном состоянии, коэффициент использования памяти в районе 60-70% Для страниц размером в более чем 10 записей, на одну страницу приходится менее 4 блоков В случае наихудшего сценария (асимметричное распределение точек) структура работает довольно плохо
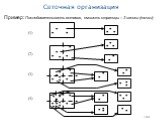
Слайд 22199
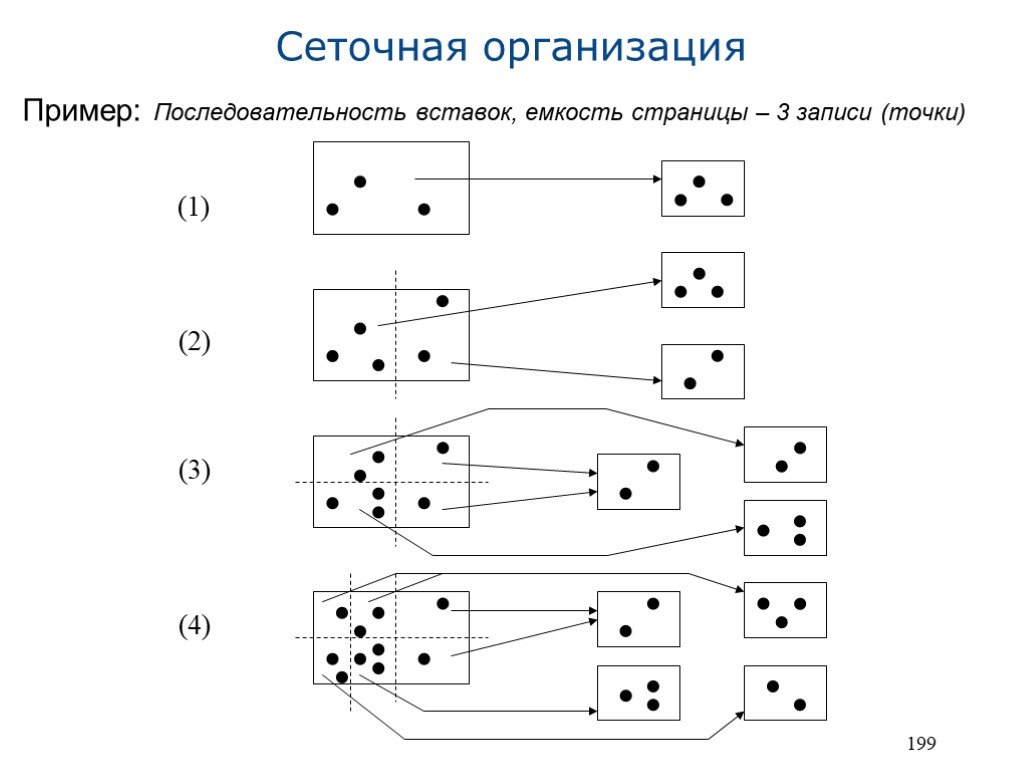
Пример: Последовательность вставок, емкость страницы – 3 записи (точки)
Слайд 23200
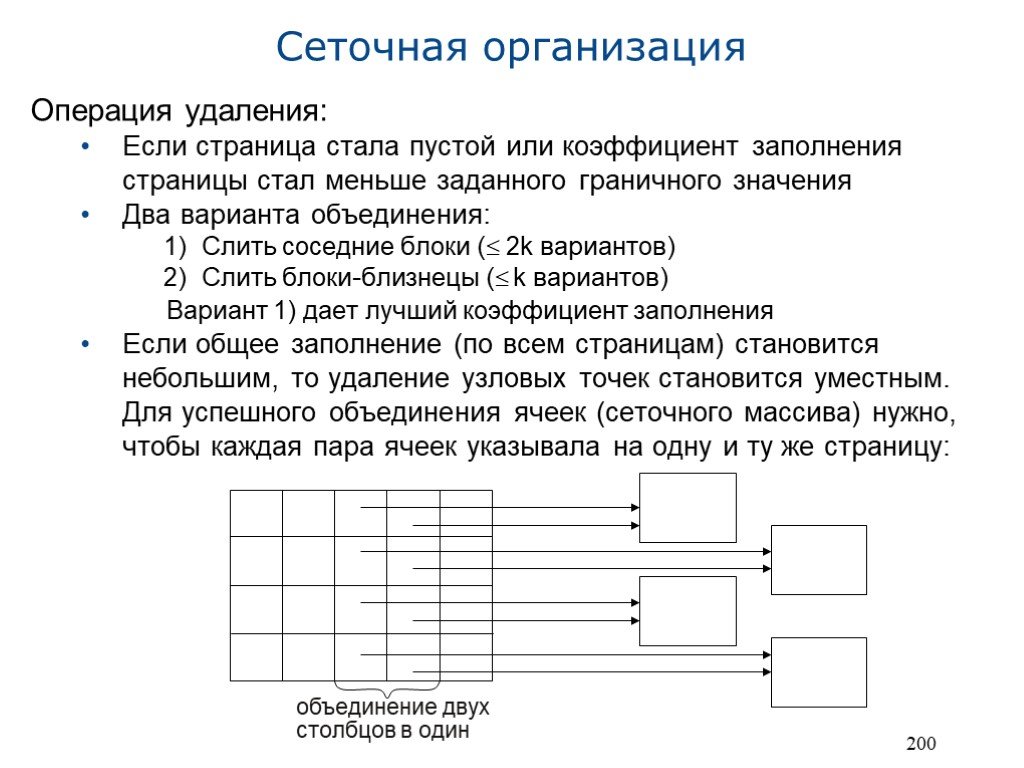
Операция удаления: Если страница стала пустой или коэффициент заполнения страницы стал меньше заданного граничного значения Два варианта объединения: Слить соседние блоки ( 2k вариантов) Слить блоки-близнецы ( k вариантов) Вариант 1) дает лучший коэффициент заполнения Если общее заполнение (по всем страницам) становится небольшим, то удаление узловых точек становится уместным. Для успешного объединения ячеек (сеточного массива) нужно, чтобы каждая пара ячеек указывала на одну и ту же страницу:
объединение двух столбцов в один
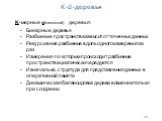
Слайд 24201 K-d-деревья
K-мерные (dimensional) деревья: Бинарные деревья Разбиение пространства зависит от точечных данных Рекурсивное разбиение вдоль одного измерения за раз Измерения по которым происходит разбиение пространства циклически чередуются Изначально, структура для представления данных в оперативной памяти Динамическая балансировка дерева возможна только при создании
Слайд 25202
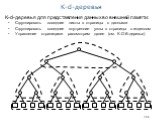
Создание сбалансированного k-d-дерева на основе заданного набора точек (пример на следующем слайде): Отсортировать точки и найти значение медианы для первого измерения (т.е. такое значение для данного измерения, что разделит множество точек на два равных подмножества) По найденному значению медианы разбить множество точек на два подмножества Найденное значение медианы сохранить в корне дерева Поддеревья строятся рекурсивно, при этом измерения по которым определяется следующие значения медиан меняются циклически Сложность: O(N logN) для N точек
Слайд 26203
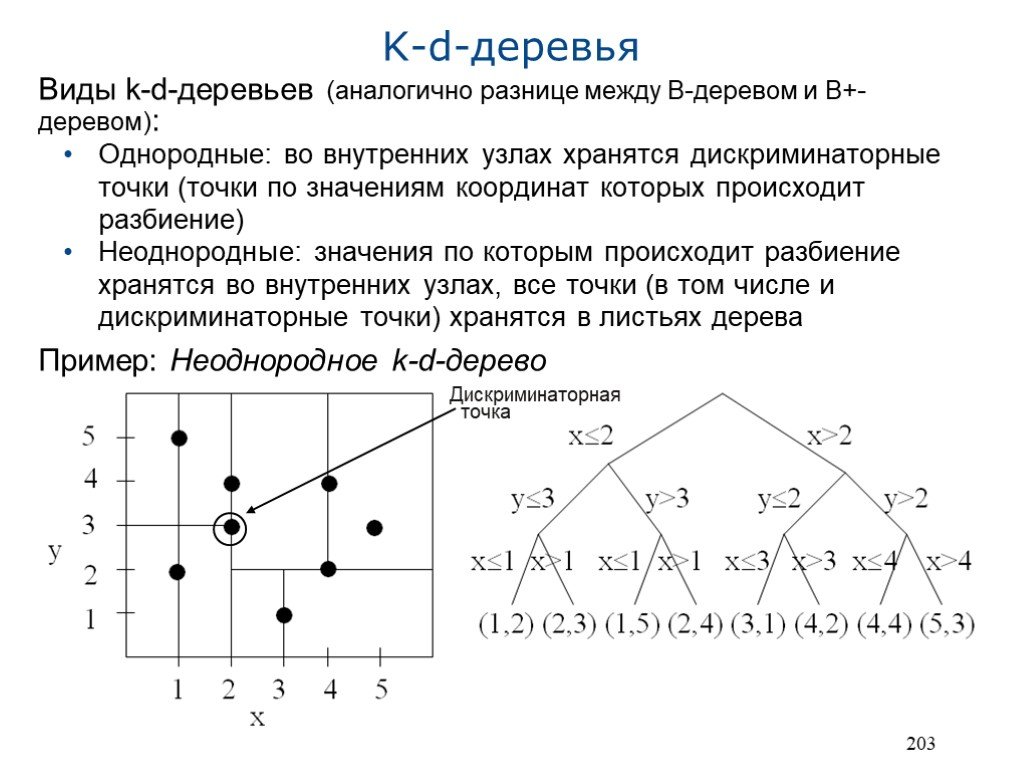
Виды k-d-деревьев (аналогично разнице между B-деревом и B+-деревом): Однородные: во внутренних узлах хранятся дискриминаторные точки (точки по значениям координат которых происходит разбиение) Неоднородные: значения по которым происходит разбиение хранятся во внутренних узлах, все точки (в том числе и дискриминаторные точки) хранятся в листьях дерева Пример: Неоднородное k-d-дерево
Дискриминаторная точка

Слайд 27204
Поиск по (неоднородному) k-d-дереву: а) Запрос по точному совпадению: Двигаться вниз от корневого узла: на i-ом уровне сравнить (i mod k)-ую координату c со значением d в узле Если c d, то продолжить движение по левому поддереву, иначе по правому Продолжая таким образом, дойти до соответствующего листа и, если все координаты совпадают, вернуть точку, хранимую листом Сложность: O(log N) как для сбалансированных, так и для иначе построенных1 деревьев б) Запрос по частичному совпадению: Если i-ое измерение не определено в запросе, то нужно просматривать как правое так и левое поддеревья на уровне s, где s mod k = i Иначе, следовать процедуре, описанной в пункте а) Если зафиксировано t (

Слайд 28205
в) Пространственный запрос: На i-ом уровне: если нижняя и верхняя границы области значений для i mod k-ой координаты меньше значения d в узле, то перейти к левому поддереву; если больше, то перейти к правому поддереву Иначе, просмотреть и правое и левое поддеревья Сложность в наихудшем случае: O(N1-1/k + R), где R – количество точек в результате запроса Вставка и удаление: Модифицированные операции вставки и удаления для двоичных деревьев поиска1 Отсутствует динамическая балансировка дерева Форма дерева зависит от порядка операций вставки Время от времени необходима реорганизация дерева 1 binary search tree (BST)
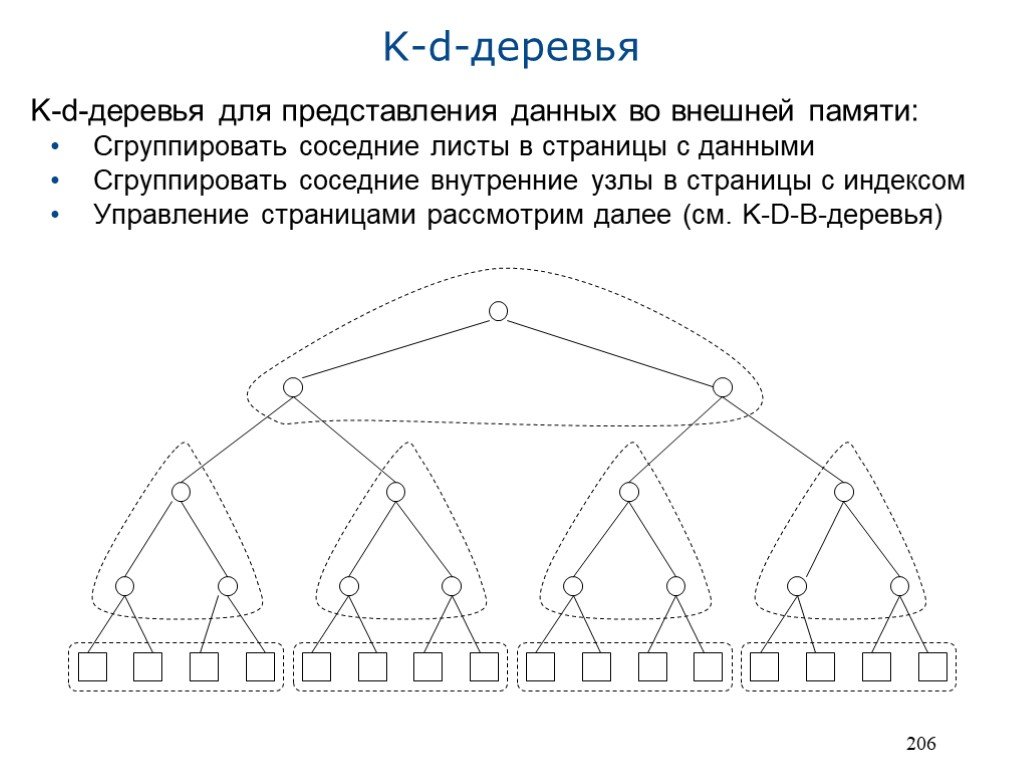
Слайд 29206
K-d-деревья для представления данных во внешней памяти: Сгруппировать соседние листы в страницы с данными Сгруппировать соседние внутренние узлы в страницы с индексом Управление страницами рассмотрим далее (см. K-D-B-деревья)

Слайд 30207
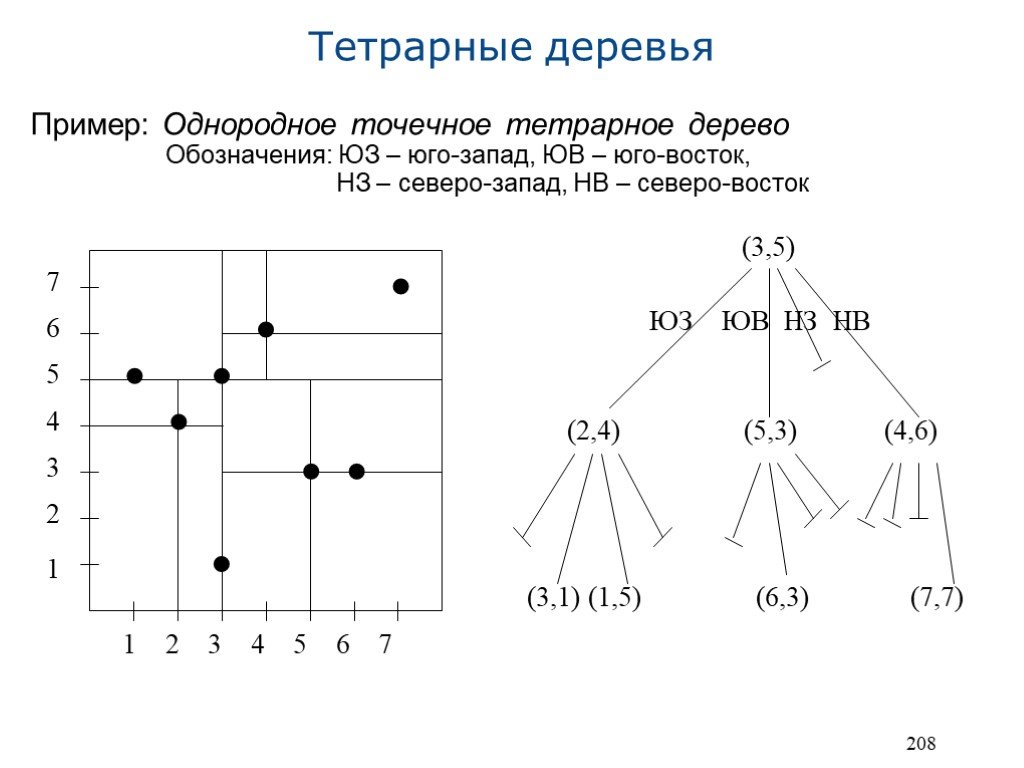
Тетрарные1 деревья
Структура для двухмерного пространства (графические изображения, карты и т.д.) Примечание: аналогичная древовидная структура но для трехмерного пространства называется октадерево2 У каждого узла дерева четыре потомка Узел дерева отображает разбиение области пространства на четыре прямоугольные непересекающиеся области а) Точечное тетрарное дерево3: K-d-дерево в котором каждые два уровня сжаты в один Дискриминаторные точки разбивают пространство по обоим измерениям (в отличие от k-d-дерева, где разбиение только по одному измерению) Можно ожидать, что высота дерева тетрарного дерева – половина высоты соответствующего k-d-дерева (но не во всех случаях) K-d-дерево в сравнении с тетрарным даст больше вариантов разбиения пространства Процесс построения дерева не гарантирует сбалансированность Обработка запросов аналогична обработке у k-d-деревьев Сложная процедура удаления из (однородного) точечного тетрарного дерева: может требоваться удаление и последующая вставка нескольких зависимых точек 1 quadtree 3 point quadtree 2 octree
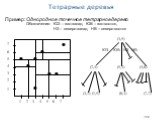
Слайд 31208
Тетрарные деревья
Пример: Однородное точечное тетрарное дерево Обозначения: ЮЗ – юго-запад, ЮВ – юго-восток, НЗ – северо-запад, НВ – северо-восток
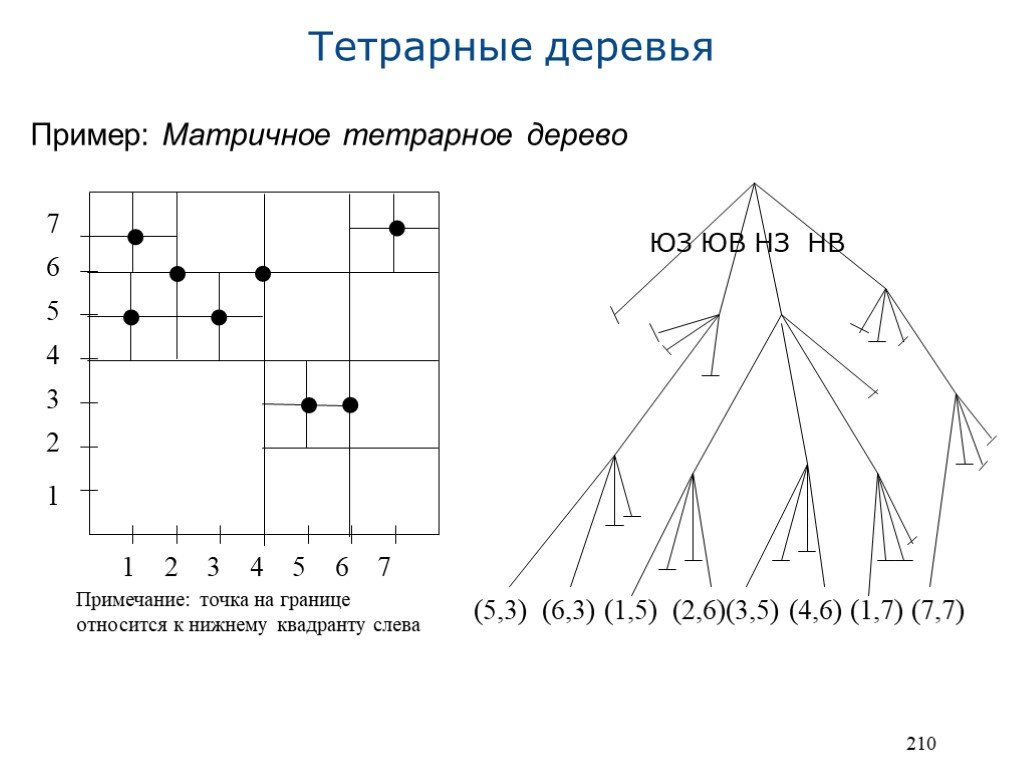
Слайд 32209
б) Матричное тетрарное дерево (MX-quadtree; matrix -> MX): Разбиение пространства происходит не по множеству точек Разбиение на четыре квадранта одинакового размера Все точки хранятся в листьях Форма дерева не зависит от порядка операций вставки Обработка запросов такая же как и в точечных тетрарных деревьях Операция вставки проста, но может потребовать еще одного разбиения Простая процедура удаления, т.к. все точки хранятся в листьях: Узел сворачивается, если все его потомки ничего не содержат Указатель на сворачиваемый узел в узле-предке устанавливается в ноль Процесс ‘свертки’ узлов может идти вплоть до вершины Демонстрация матричных тетрарных деревьев: http://donar.umiacs.umd.edu/quadtree/points/mxquad.html
Слайд 33210
Пример: Матричное тетрарное дерево
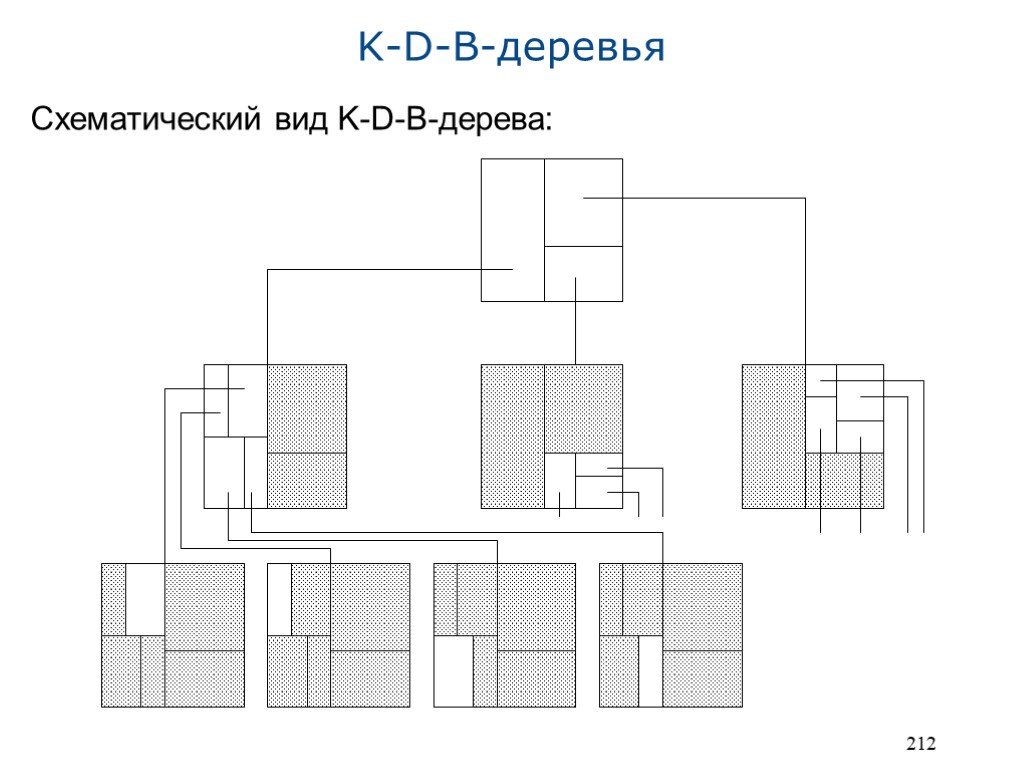
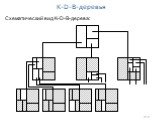
Слайд 34211 K-D-B-деревья
K-d- и тетрарные деревья предназначены (преимущественно) для представления данных в оперативной памяти K-D-B-дерево [4] – одна из первых структур многомерных данных для внешней памяти Заимствованы свойства k-d-деревьев Позже были разработаны более совершенные древовидные структуры Структура K-D-B-дерева: Дерево с множественным ветвлением Два типа узлов: Страницы с областями: Внутренние узлы, представляющие собой индекс Область – прямоугольная область в k-мерном пространстве Страница с областью описывает разбиение области на подобласти Разбиение на подобласти аналогично разбиению для k-d-деревьев Страницы с точками: Листья, непосредственно содержащие точки (k координатных значений на точку)
Слайд 35212
Схематический вид K-D-B-дерева:

Слайд 36213
Поиск по K-D-B-дереву: Запросы по точному совпадению: движение по дереву до листа, содержащим точки в искомой области Запросы по частичному совпадению и пространственные запросы: движение по дереву вдоль нескольких ветвей, т.к. область, задаваемая запросом, может пересекаться с несколькими подобластями, хранимыми деревом Вставка точки: Вставить в соответствующий лист, если в нем есть место Если лист переполняется, то необходимо разбиение (например, для этого может использоваться медианное значение для ‘очередного’ измерения) Если переполняется внутренний узел, то необходимо разбиение, которое разделит подобласти, задаваемые двумя новыми (заменяющими старый) узлами. Для подобласти возможны три позиции относительно плоскости разбиения: Если подобласть слева от плоскости, то отнести подобласть к левому узлу Аналогично если справа Если плоскость разбивает подобласть, то разбить подобласть на две половины, слева и справа от плоскости, и внести изменения в соответствующие узлы-потомки Переполнение может распространяться как вниз так и вверх по дереву

Слайд 37214
Удаление точки: Найти и удалить из соответствующего листа Незаполненность: коэффициент заполнения страницы меньше определенного значения Затруднение: область с которой возможно объединение может быть разбита на подобласти (т.е. описываться на нескольких страницах) Выход: Перестроить эту часть дерева Коэффициент использования памяти: Около 60% 10%, т.е. неплохой Заключение: Далеко не идеальная структура После 1981г. появились многомерные деревья (для внешней памяти) лучше, чем K-D-B-деревья
![215. Другие типы многомерных деревьев. TV-дерево1 [5]: Специально предназначено для представления точечных данных в пространствах очень большой размерности; например, текстовых бд (векторы терминов, SVD-трансформированные вектора, сигнатуры) Затруднения с пространствами большой размерности: Области 215. Другие типы многомерных деревьев. TV-дерево1 [5]: Специально предназначено для представления точечных данных в пространствах очень большой размерности; например, текстовых бд (векторы терминов, SVD-трансформированные вектора, сигнатуры) Затруднения с пространствами большой размерности: Области](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen38.jpg)
Слайд 38215
Другие типы многомерных деревьев
TV-дерево1 [5]: Специально предназначено для представления точечных данных в пространствах очень большой размерности; например, текстовых бд (векторы терминов, SVD-трансформированные вектора, сигнатуры) Затруднения с пространствами большой размерности: Области сильно перекрываются; совпадение большей части координатных значений у рядом находящихся точек В индексе должны использоваться такие координатные значения, что наилучшим образом разделяют подмножества точек Каждый узел содержит “центр” и “радиус” У каждого узла есть набор “активных измерений”, которые используются при определении расстояний между точками Телескопирование: при разбиении число активных измерений у получившихся подмножеств может вырасти; при вставке число активных измерений может уменьшиться Крайне удобно для поиска p ближайших соседей 1 Telescopic-Vector tree
![216. M-дерево [6]: Предназначено для объектов в метрическом пространстве: Функция расстояния (метрика) должна быть: симметричной, неотрицательной, и для нее должно выполняться неравенство треугольника (см. математическое определение метрического пр-ва) Разработано специально для мультимедийных баз д 216. M-дерево [6]: Предназначено для объектов в метрическом пространстве: Функция расстояния (метрика) должна быть: симметричной, неотрицательной, и для нее должно выполняться неравенство треугольника (см. математическое определение метрического пр-ва) Разработано специально для мультимедийных баз д](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen39.jpg)
Слайд 39216
M-дерево [6]: Предназначено для объектов в метрическом пространстве: Функция расстояния (метрика) должна быть: симметричной, неотрицательной, и для нее должно выполняться неравенство треугольника (см. математическое определение метрического пр-ва) Разработано специально для мультимедийных баз данных; расстояние между объектами вычисляется на основе мультимедийных характеристик объекта Является метрическим деревом: объекты не имеют абсолютных позиций в пространстве, вместо используются относительные расстояния между объектами Внутренние узлы содержат так называемые направляющие (routing) объекты, а все потомки этого узла содержат объекты, лежащие в пределах определенного расстояния от этого направляющего объекта M-деревья – сбалансированные деревья; периодическая реорганизация не требуется Виды запросов: нахождение ближайшего соседа, нахождение p ближайших соседей, пространственные запросы Возможна оптимизация дерева с целью уменьшения нагрузки на процессор (вычисление расстояний) и операций ввод/вывода

Слайд 40217 Упражнения
Рассмотрим дискретное целочисленное трехмерное пр-во - (0..7, 0..7, 0..7). Отсортируйте следующие точки в Z-порядке: (4, 2, 5), (1, 3, 4), (3, 0, 6), (2, 0, 7), (5, 2, 1), (7, 1, 2), (1, 4, 3), (2, 6, 3). Определите расстояния между соседними точками в отсортированной последовательности (семь расстояний). Произошла ли кластеризация точек? Для следующих точек: (4, 6), (1, 5), (5, 3), (5, 5), (3, 4), (6, 1), (7, 6), (2, 1) построить: неоднородное тетрарное дерево однородное тетрарное дерево
![218. Ссылки на литературу. [1] Böhm et al. Searching in High-Dimensional Spaces – Index Structures for Improving the Performance of Multimedia Databases. ACM Computing Surveys, 33(3), 2001 [2] Gaede and Günther. Multidimensional Access Methods. ACM Computing Surveys, 30(2), 1998 [3] Bayer. The unive 218. Ссылки на литературу. [1] Böhm et al. Searching in High-Dimensional Spaces – Index Structures for Improving the Performance of Multimedia Databases. ACM Computing Surveys, 33(3), 2001 [2] Gaede and Günther. Multidimensional Access Methods. ACM Computing Surveys, 30(2), 1998 [3] Bayer. The unive](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen41.jpg)
Слайд 41218
Ссылки на литературу
[1] Böhm et al. Searching in High-Dimensional Spaces – Index Structures for Improving the Performance of Multimedia Databases. ACM Computing Surveys, 33(3), 2001 [2] Gaede and Günther. Multidimensional Access Methods. ACM Computing Surveys, 30(2), 1998 [3] Bayer. The universal B-Tree for multidimensional Indexing: General Concepts. WWCA-97, 1997 [4] Robinson. The K-D-B-tree: a search structure for large multidimensional dynamic indexes. SIGMOD-1981, 1981 [5] Lin et al. The TV-tree: An index structure for high-dimensional data. VLDB Journal, 3(4), 1994 [6] Ciaccia et al. M-tree: An Efficient Access Method for Similarity Search in Metric Spaces. VLDB-1997, 1997













































![195. Запрос по точному совпадению: С помощью шкал найти точное расположение нужной записи в (k-мерном) сеточном массиве (возможно потребуется обращение к диску) По указателю перейти к нужной странице Пример: Двухмерное пространство: Запрос: найти . [0, 1000, 1500, 1750, 1875, 2000]. [a, g, m, t, z] 195. Запрос по точному совпадению: С помощью шкал найти точное расположение нужной записи в (k-мерном) сеточном массиве (возможно потребуется обращение к диску) По указателю перейти к нужной странице Пример: Двухмерное пространство: Запрос: найти . [0, 1000, 1500, 1750, 1875, 2000]. [a, g, m, t, z]](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen18.jpg)













![211 K-D-B-деревья. K-d- и тетрарные деревья предназначены (преимущественно) для представления данных в оперативной памяти K-D-B-дерево [4] – одна из первых структур многомерных данных для внешней памяти Заимствованы свойства k-d-деревьев Позже были разработаны более совершенные древовидные структуры 211 K-D-B-деревья. K-d- и тетрарные деревья предназначены (преимущественно) для представления данных в оперативной памяти K-D-B-дерево [4] – одна из первых структур многомерных данных для внешней памяти Заимствованы свойства k-d-деревьев Позже были разработаны более совершенные древовидные структуры](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen34.jpg)


![215. Другие типы многомерных деревьев. TV-дерево1 [5]: Специально предназначено для представления точечных данных в пространствах очень большой размерности; например, текстовых бд (векторы терминов, SVD-трансформированные вектора, сигнатуры) Затруднения с пространствами большой размерности: Области 215. Другие типы многомерных деревьев. TV-дерево1 [5]: Специально предназначено для представления точечных данных в пространствах очень большой размерности; например, текстовых бд (векторы терминов, SVD-трансформированные вектора, сигнатуры) Затруднения с пространствами большой размерности: Области](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen38.jpg)
![216. M-дерево [6]: Предназначено для объектов в метрическом пространстве: Функция расстояния (метрика) должна быть: симметричной, неотрицательной, и для нее должно выполняться неравенство треугольника (см. математическое определение метрического пр-ва) Разработано специально для мультимедийных баз д 216. M-дерево [6]: Предназначено для объектов в метрическом пространстве: Функция расстояния (метрика) должна быть: симметричной, неотрицательной, и для нее должно выполняться неравенство треугольника (см. математическое определение метрического пр-ва) Разработано специально для мультимедийных баз д](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen39.jpg)

![218. Ссылки на литературу. [1] Böhm et al. Searching in High-Dimensional Spaces – Index Structures for Improving the Performance of Multimedia Databases. ACM Computing Surveys, 33(3), 2001 [2] Gaede and Günther. Multidimensional Access Methods. ACM Computing Surveys, 30(2), 1998 [3] Bayer. The unive 218. Ссылки на литературу. [1] Böhm et al. Searching in High-Dimensional Spaces – Index Structures for Improving the Performance of Multimedia Databases. ACM Computing Surveys, 33(3), 2001 [2] Gaede and Günther. Multidimensional Access Methods. ACM Computing Surveys, 30(2), 1998 [3] Bayer. The unive](https://prezentacii.org/upload/cloud/19/04/139279/images/thumbs/screen41.jpg)