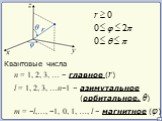
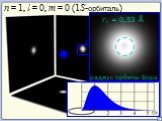
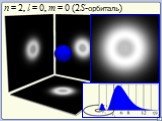
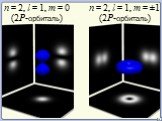
Презентация "Уравнение Шредингера" по физике – проект, доклад
Презентацию на тему "Уравнение Шредингера" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 53 слайд(ов).
Слайды презентации
Список похожих презентаций
Уравнение Шредингера. Элементы квантовой механики
Общее уравнение Шредингера. ШРЁДИНГЕР, ЭРВИН австрийский физик. Нобелевская премия по физике 1933 ( с П.Дираком). Стационарное уравнение Шредингера. ...Уравнение состояния идеального газа. Газовые законы
Макроскопические параметры – это…:. Масса, давление, объем, температура. давление, объем, температура. Состояние газа данной массы характеризуется ...Уравнение состояния идеального газа
Цель урока:. Вывести зависимость между макроскопическими параметрами, характеризующими состояние газа. Проверить экспериментально уравнение состояния ...Уравнение состояния идеального газа
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой T. Между ...Уравнение состояния идеального газа
Физический диктант. Что называют идеальным газом? Какие параметры называют макроскопическими? Как определяется давление идеального газа? С чем связывают ...Уравнение Максвелла и его свойства
. . . . Рассмотрим цепь переменного тока, содержащую плоский конденсатор. . . . - Закон полного тока. . . . Закон полного тока. Теорема Гаусса. . ...Уравнение Максвелла для электромагнитного поля
Первое уравнение Максвелла. представляет собой закон полного тока: Смысл первого уравнения Максвелла состоит в том, что любой ток проводимости I порождает ...Уравнение движения
. . . . . ...Температура. Уравнение состояния
Если обозначить среднюю энергию молекулы, приходящуюся на одну степень свободы через , то полная кинетическая энергия поступательного движения всех ...Уравнение состояния идеального газа. Газовые законы
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА ГАЗОВЫЕ ЗАКОНЫ. На титульный лист. Состояние данной массы газа характеризуется тремя макроскопическими параметрами: ...Закон сохранения внутренней энергии. Уравнение теплового баланса
Цели урока. познакомиться с законом сохранения внутренней энергии и уравнением теплового баланса; научиться применять полученные знания при решении ...Поверхностное натяжение. Уравнение Бернулли
Свойства жидкости и газа. Жидкие тела характерны тем, что не оказывают сопротивления сдвигу и поэтому способны изменять свою форму под воздействием ...Лампы накаливания физика
Актуальность. 2 июля 2009 года Президент России Дмитрий Медведев, выступая на заседании президума Госсовета по вопросам повышения энергоэффективности ...Квантовая физика
П Л А Н 1. СТО А. Эйнштейна. 2. Тепловое излучение. 3. Фотоэффект. 4. Люминесценция. 5. Химическое действие света. 6. Световое давление. 7. Физический ...Капиллярные явления физика
Ищем:. Капиллярные явления Модель капиллярного вечного двигателя Объяснение невозможности создания такого двигателя. Капиллярные явления. Заключаются ...Интересная физика
Интересная физика. Предметная область Физика, информатика Участники: учащиеся 7 – 11 классов, учителя, родители. Цели и задачи: Изучить физику в более ...Свободное падение физика
Свободное падение тел впервые исследовал Галилей, который установил, что свободно падающие тела движутся равноускоренно с одинаковым для всех тел ...Строение атома Квантовая физика
строение атома 11 квантовая физика ФИЗИКА КЛАСС. Данный урок проводится по типу телевизионной передачи…. Квантовая физика. Строения атома. ВЫХОД. ...Радиосвязь физика
Вопросы. Что такое и колебательный контур? Для чего он предназначен Какие превращения энергии происходят в колебательном контуре? Чем отличается открытый ...Презентации и физика
Актуальность. «Главная задача современной школы - это раскрытие способностей каждого ученика, воспитание личности, готовой к жизни в высокотехнологичном, ...Конспекты
Уравнение состояния идеального газа
Власова Надежда Ивановна. учитель физики. МКОУ Петропавловская СОШ. Тема урока. «Уравнение состояния идеального газа». ...Уравнение состояния идеального газа
Уравнение состояния идеального газа. . Цель. :. сформировать умение описывать состояние термодинамической системы данной массы газа с помощью 3 макропараметров. ...Уравнение состояния идеального газа
Урок физики. Тема:. . Уравнение состояния идеального газа. Цели:. 1. Добиться понимания уравнения состояния идеального газа и научить решать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 ноября 2018
Категория:Физика
Содержит:53 слайд(ов)
Поделись с друзьями:
Скачать презентацию





























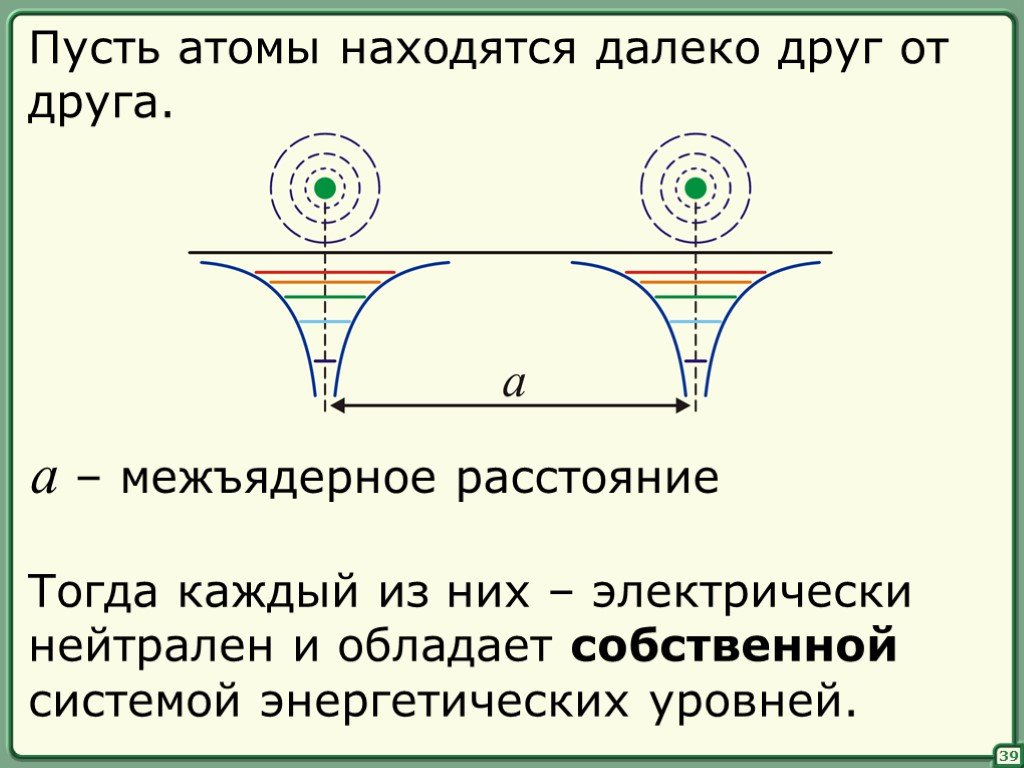
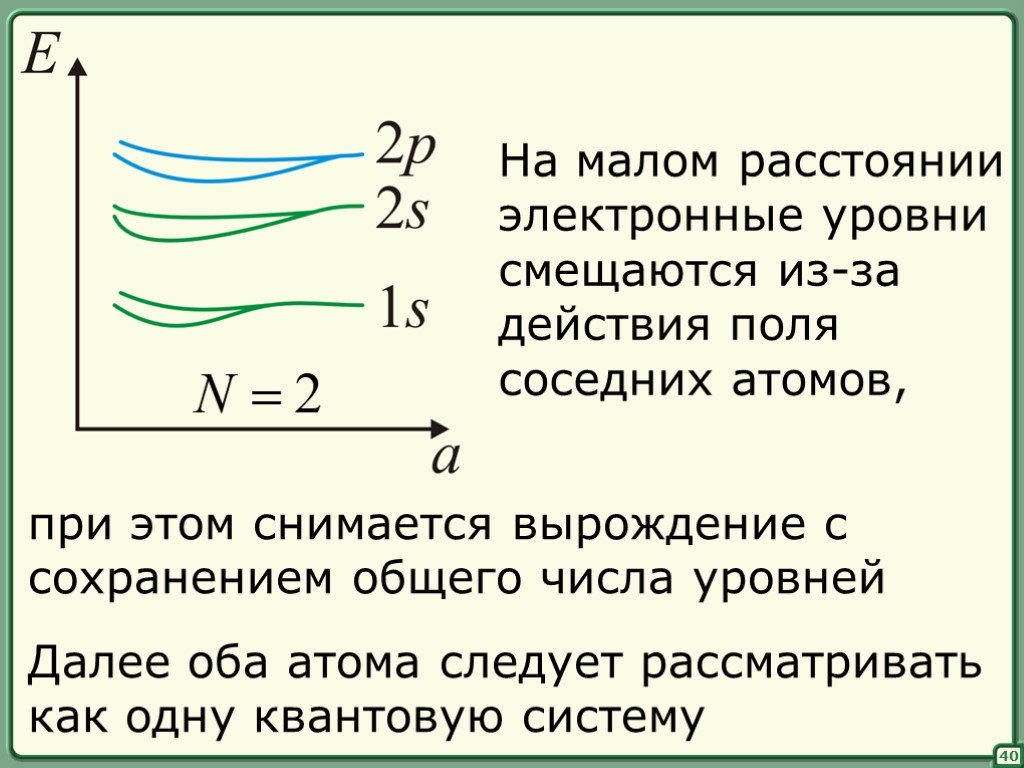

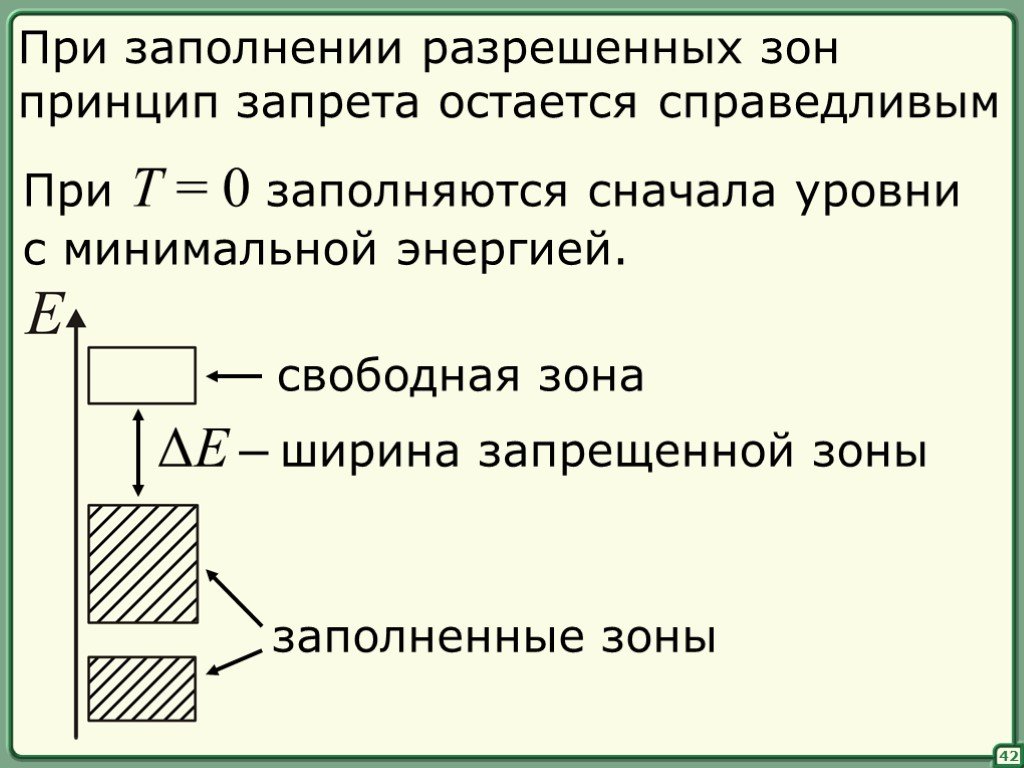





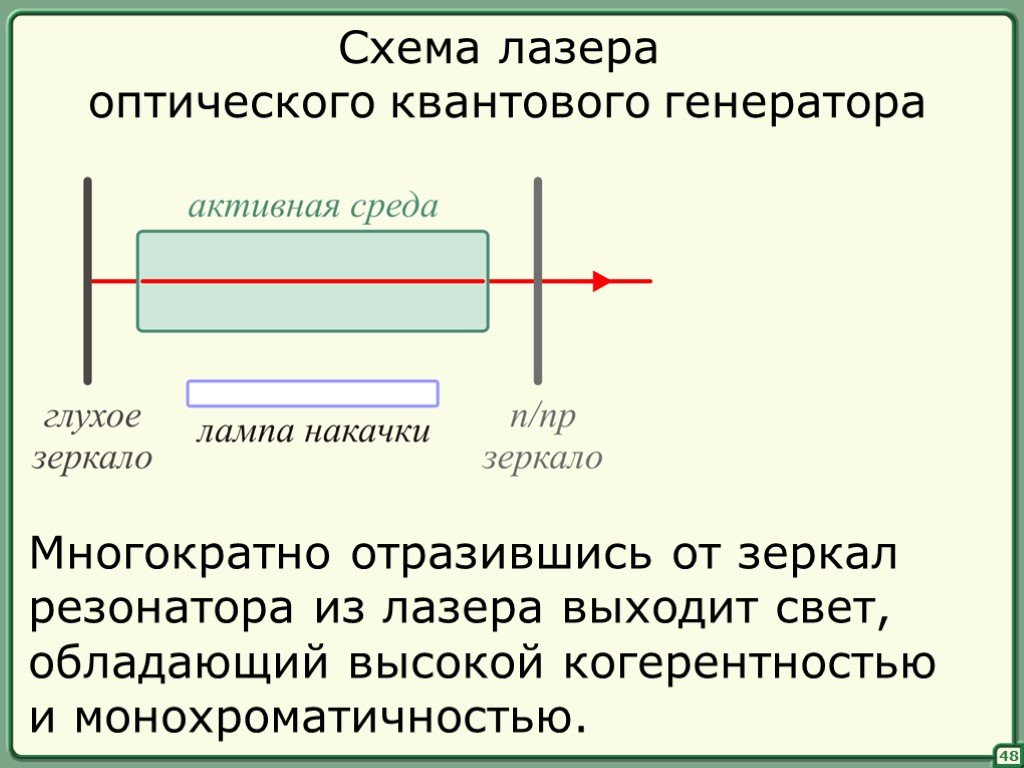











![Поскольку (интенсивность) – величина, пропорциональная вероятности обнаружить частицу, – вероятность обнаружения частицы в интервале [x, x+dx]. Во всем пространстве. то необходимо ввести нормировку. Поскольку (интенсивность) – величина, пропорциональная вероятности обнаружить частицу, – вероятность обнаружения частицы в интервале [x, x+dx]. Во всем пространстве. то необходимо ввести нормировку.](https://prezentacii.org/upload/cloud/18/11/94644/images/thumbs/screen7.jpg)