Слайд 1Молекулярная физика и термодинамика Дмитриевский Александр Александрович 2010
Слайд 2Литература: 1. Кудрявцев Б.Б., Курс физики: Теплота и молекулярная физика. – М.: Учпедгиз, 1960. 210 с. 2. Савельев И.В. Курс общей физики Т. 1, Механика, колебания и волны, молекулярная физика, - М.: Наука, 1966. 404 с. 3. Кикоин И.К., Кикоин А.К. Молекулярная физика.-М.: Наука, 1976. 500 с. 4. Матвеев А.Н. Молекулярная физика.- М.: Высшая школа. 5. Сивухин Д.В. Общий курс физики, т.2. - М.: Наука. 6. Яковлев В.Ф. физики: Теплота и молекулярная физика. 7. Волькенштейн В.С. Сборник задач по общему курсу физики.- М. 8. Сборник задач по общему курсу физики: Термодинамика и молекулярная физика // В.Л. Гинзбург. Л.М.Левин, Д.В.,Сивухин, И.Я. Яковлев. - М.: Наука, 1976.- 208 с.
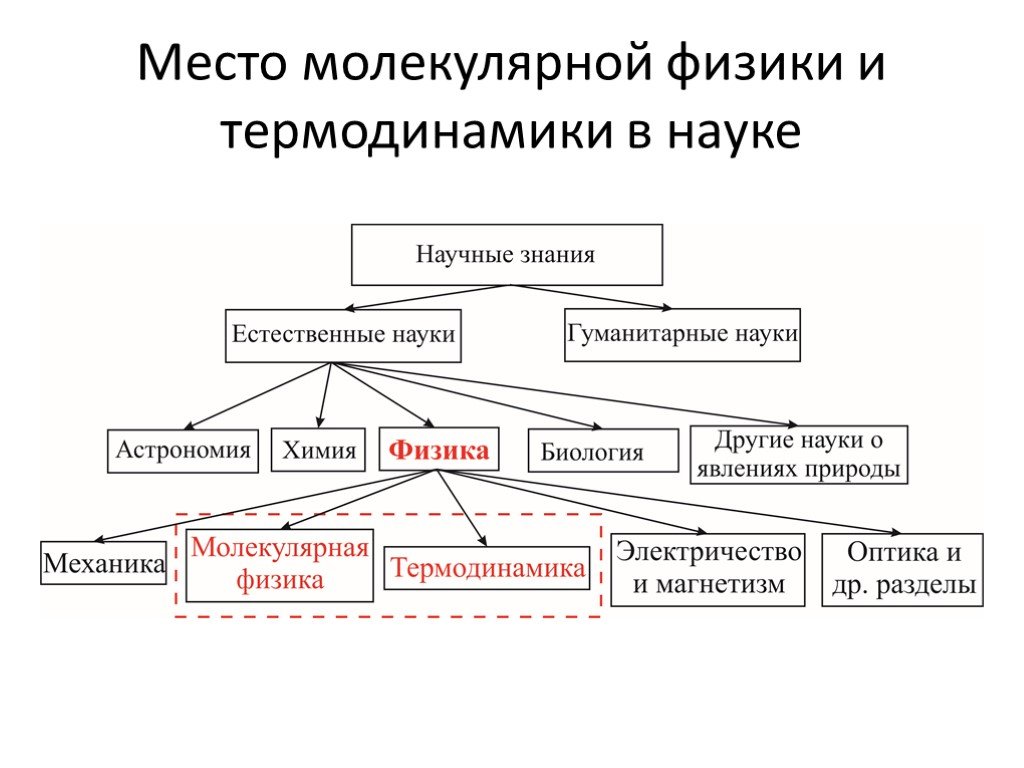
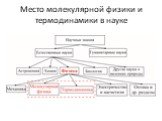
Слайд 3Место молекулярной физики и термодинамики в науке
Слайд 4§ 1. Молекулярно кинетическая теория газов и термодинамика
Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя из так называемых молекулярно-кинетических представлений. Согласно этим представлениям, любое тело – твердое, жидкое или газообразное – состоит из большого количества весьма малых обособленных частиц – молекул. Молекулы всякого вещества находятся в беспорядочном, хаотическом, не имеющим какого-либо преимущественного направления движении. Его интенсивность зависит от температуры вещества.
Слайд 5Броуновское движение
Броуновское движение - тепловое движение взвешенных в жидкости или газе частиц.
Слайд 6Из истории развития МКТ
Фундаментом МКТ является атомистическая гипотеза: все тела в природе состоят из мельчайших структурных единиц – атомов и молекул.
Слайд 7Молекулярно-кинетическая теория ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются на опыте (Р, Т, V и др.) как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц, следовательно другое название – статистическая физика.
Изучением различных свойств тел и изменений состояния вещества занимается также термодинамика. Однако в отличие от МКТ термодинамика изучает макроскопические свойства тел и явлений природы, не интересуясь их микроскопической картиной. Не вводя в рассмотрение молекулы и атомы, не входя в микроскопическое рассмотрение процессов, термодинамика позволяет делать целый ряд выводов относительно их протекания.

Слайд 8§ 2. Состояние системы. Процесс.
Системой тел, или просто системой называется совокупность рассматриваемых тел. Пример системы: жидкость + пар. Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.д. Подобные величины, характеризующие состояние системы, называют параметрами состояния. Не всегда какой-либо параметр имеет определенное значение. Если например, температура в разных точках неодинакова, то телу нельзя приписать определенное значение параметра Т. В этом случае состояние называется неравновесным. Если такое тело изолировать от других тел и предоставить самому себе, то Т выровняется и примет одинаковое для всех точек значение Т – тело перейдет в равновесное состояние. Итак, равновесным состоянием системы называется такое состояние при котором все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго. Имеют место флуктуации…

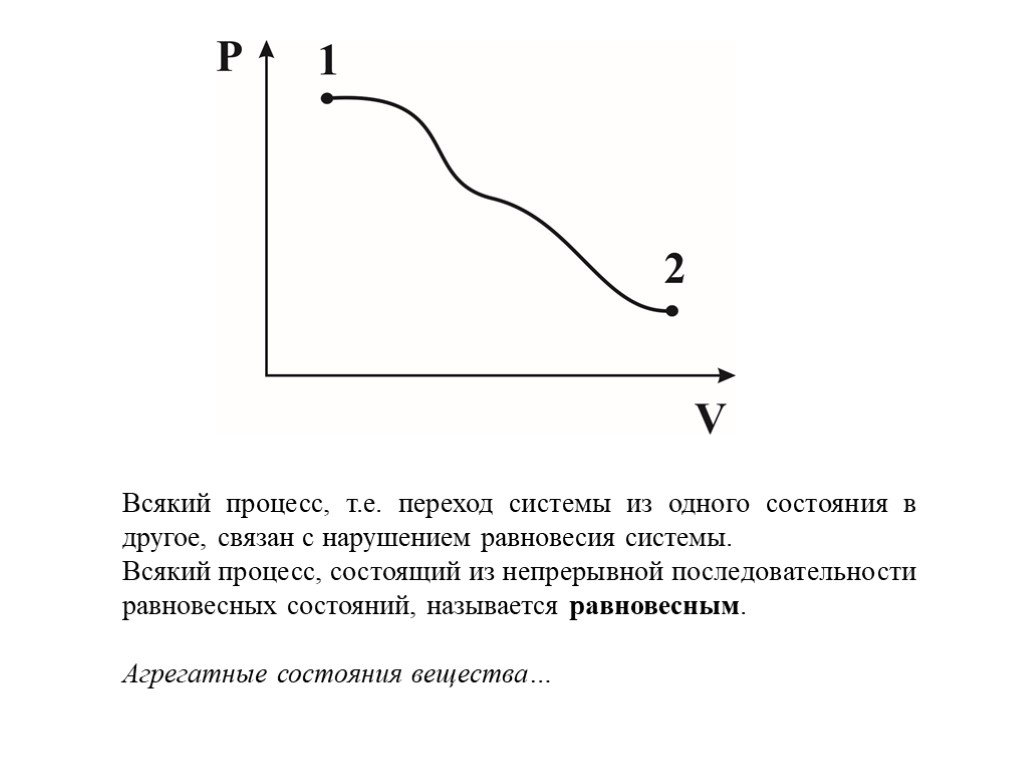
Слайд 9Всякий процесс, т.е. переход системы из одного состояния в другое, связан с нарушением равновесия системы. Всякий процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным. Агрегатные состояния вещества…
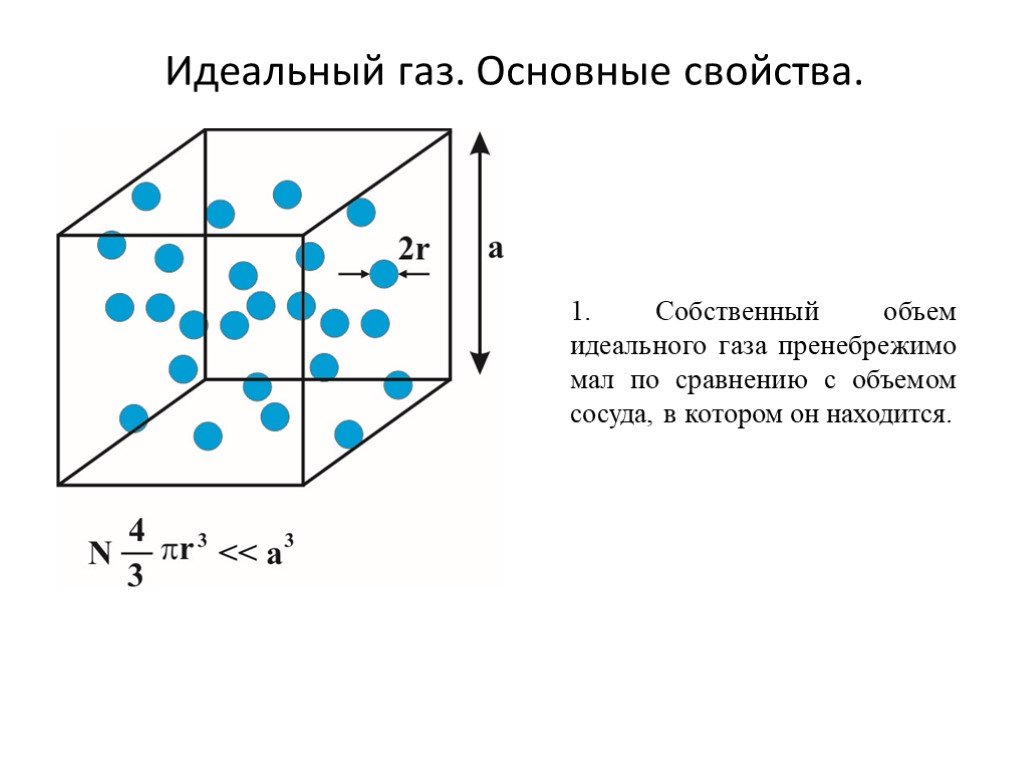
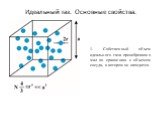
Слайд 10Идеальный газ. Основные свойства.
1. Собственный объем идеального газа пренебрежимо мал по сравнению с объемом сосуда, в котором он находится.
Слайд 112. Между молекулами идеального газа отсутствуют силы взаимодействия.
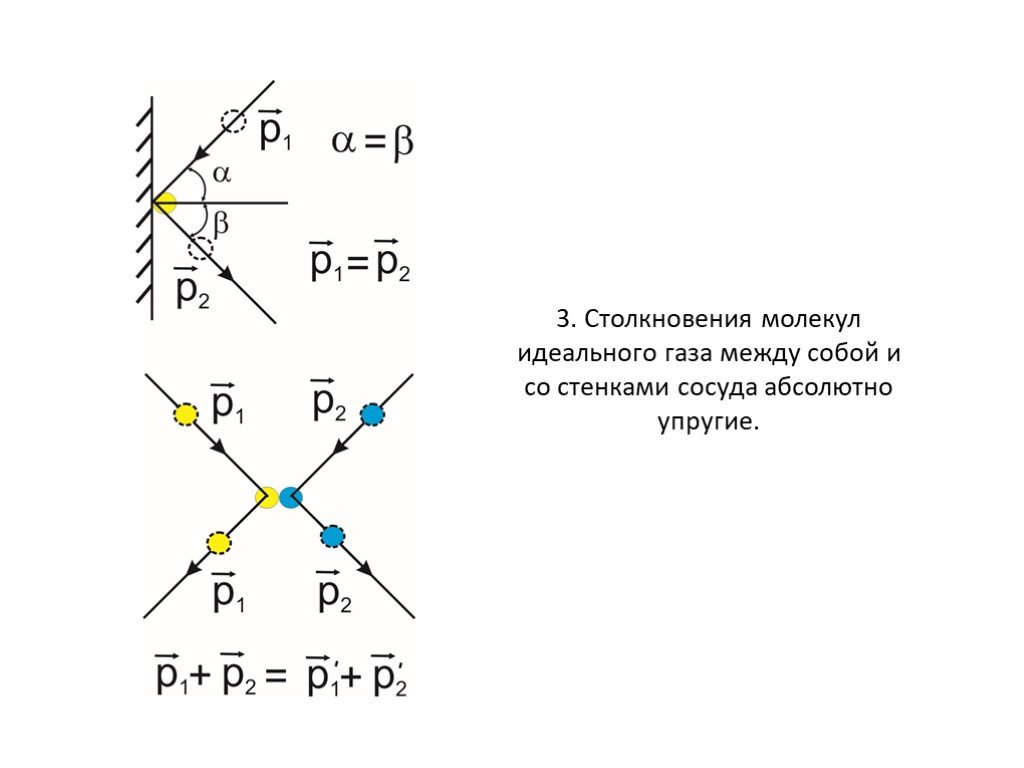
Слайд 123. Столкновения молекул идеального газа между собой и со стенками сосуда абсолютно упругие.
Слайд 13§ 3. Уравнение состояния идеального газа
Состояние некоторой массы газа определяется значением трех параметров: Р, Т, и V. Эти параметры связаны между собой. Изменение одного ведет к изменению другого. Связь может быть задана аналитически: F(Р, Т, V) = 0 или P = f(V,T)
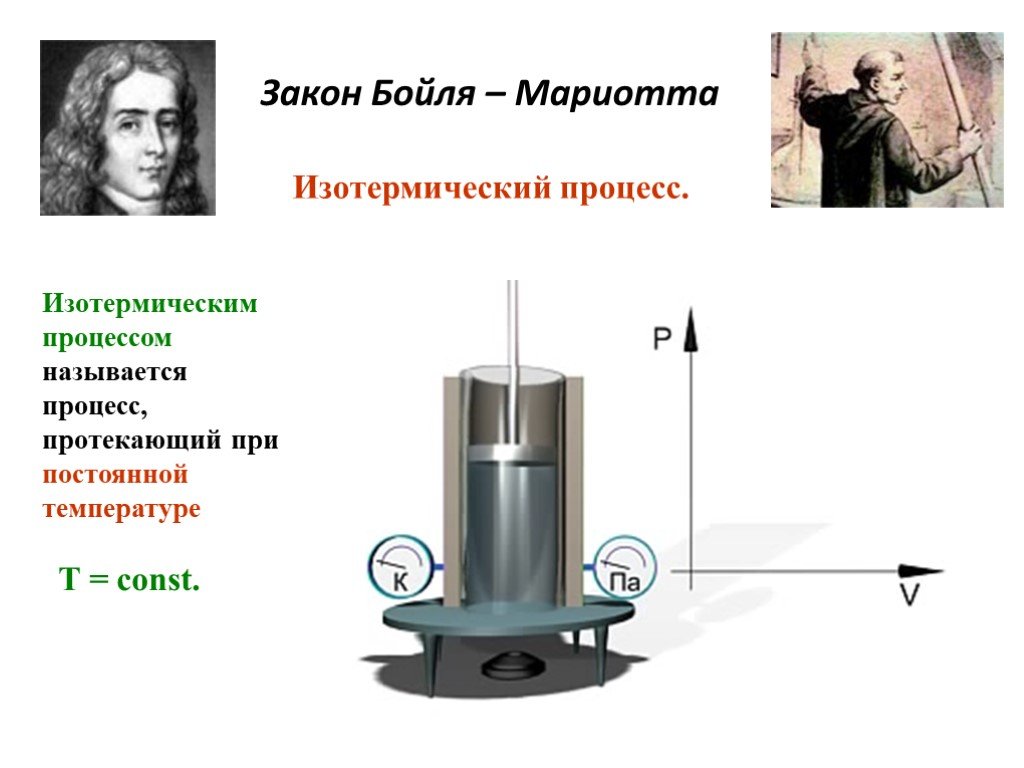
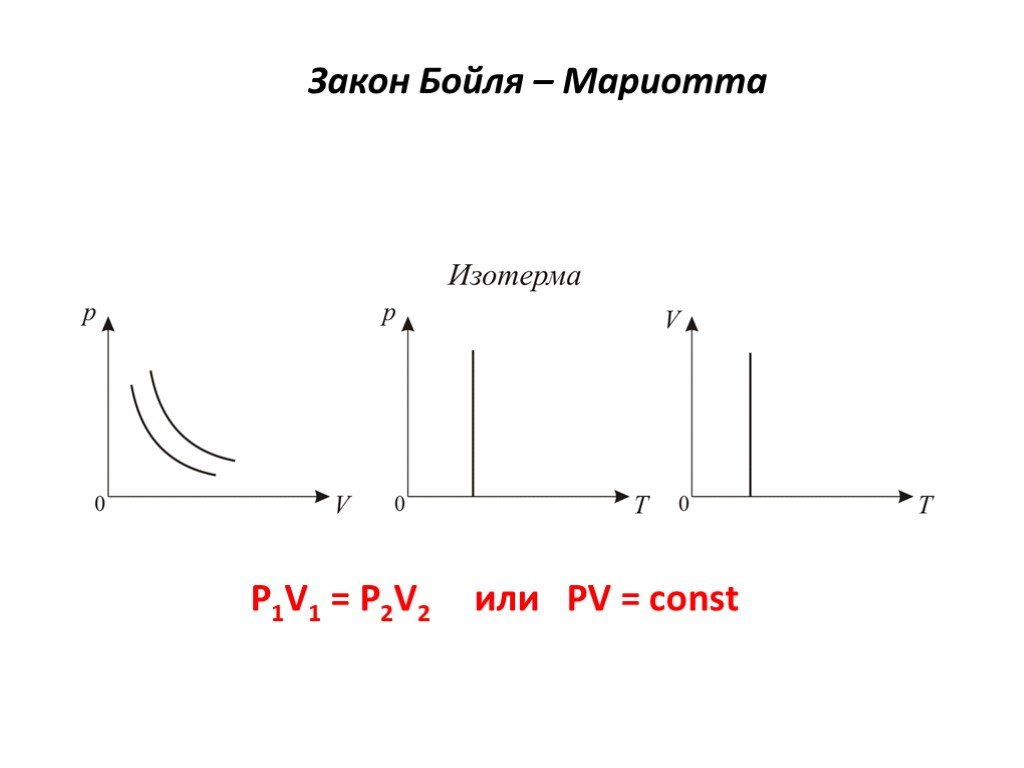
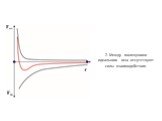
Слайд 14Закон Бойля – Мариотта
Изотермический процесс.
Изотермическим процессом называется процесс, протекающий при постоянной температуре
T = const.
Слайд 15P1V1 = P2V2 T1 T2 T1 < T2 или PV = const
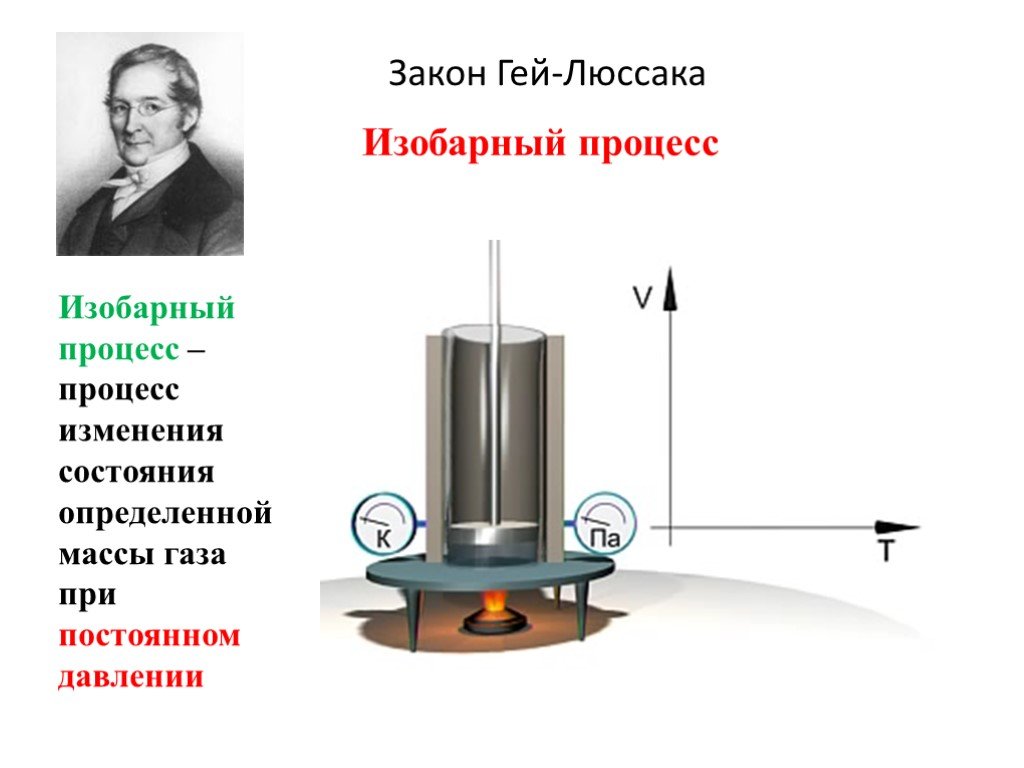
Слайд 16Закон Гей-Люссака
Изобарный процесс – процесс изменения состояния определенной массы газа при постоянном давлении
Изобарный процесс
Слайд 17P = const V = V0 + kt При t = - 273 V = 0; тогда 0 = V0 – 273k отсюда k = V0/273 α = 1/273 V = V0 (1+αt)
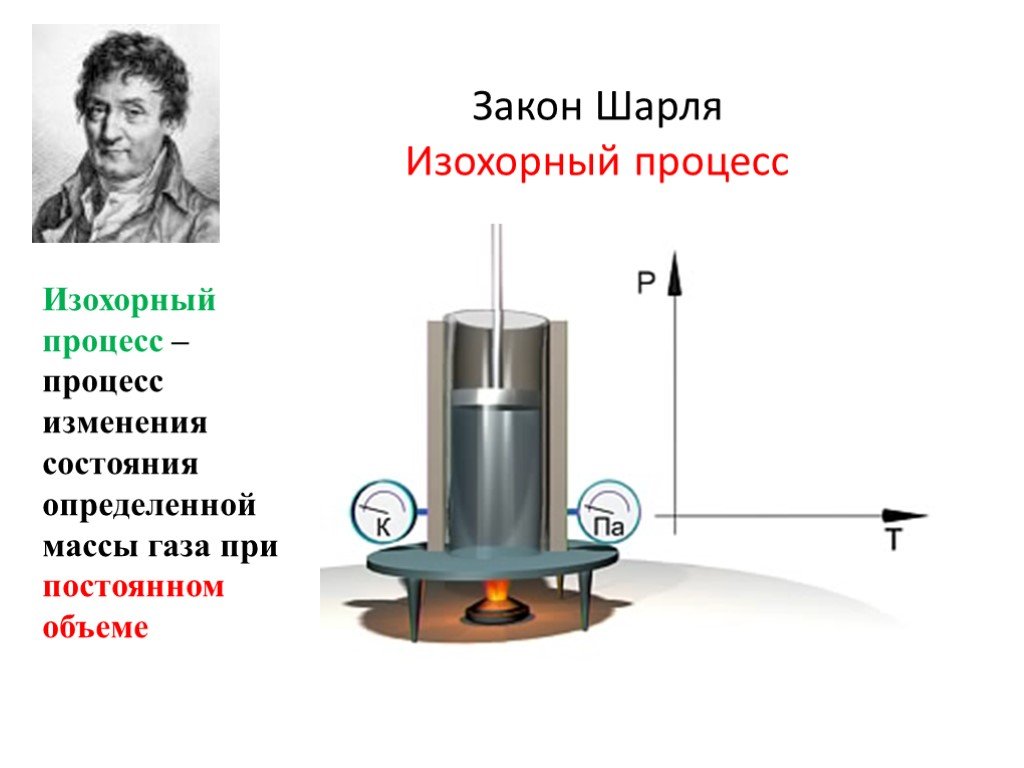
Слайд 18Закон Шарля Изохорный процесс
Изохорный процесс – процесс изменения состояния определенной массы газа при постоянном объеме
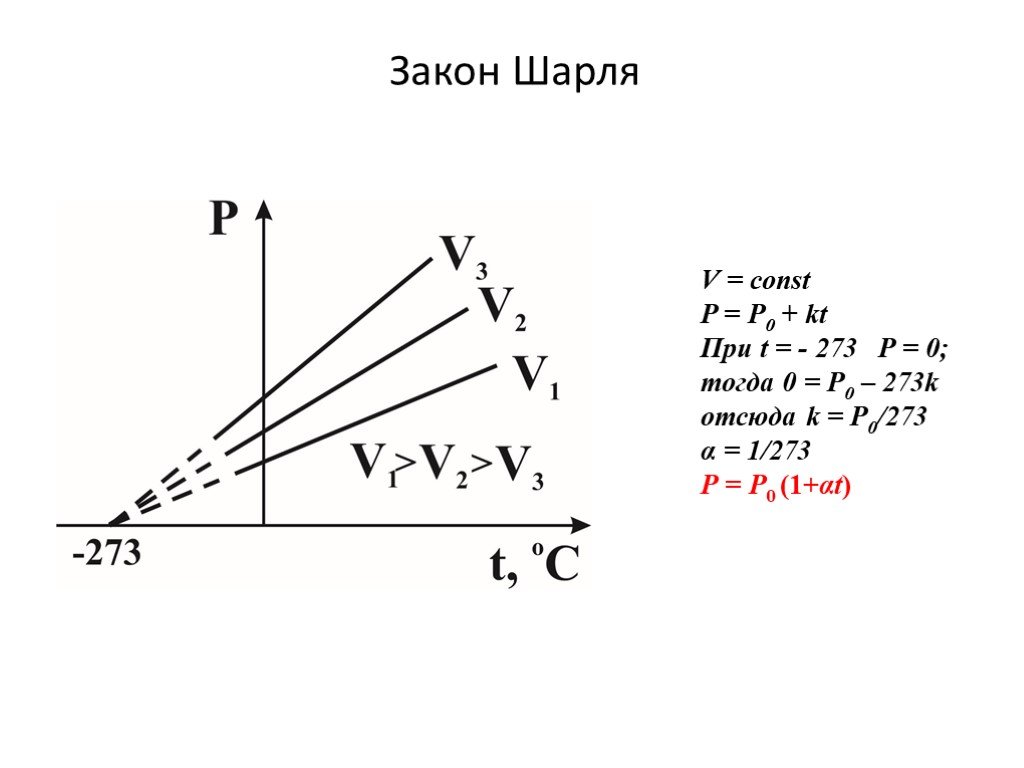
Слайд 19Закон Шарля
V = const P = P0 + kt При t = - 273 P = 0; тогда 0 = P0 – 273k отсюда k = P0/273 α = 1/273 Р = Р0 (1+αt)
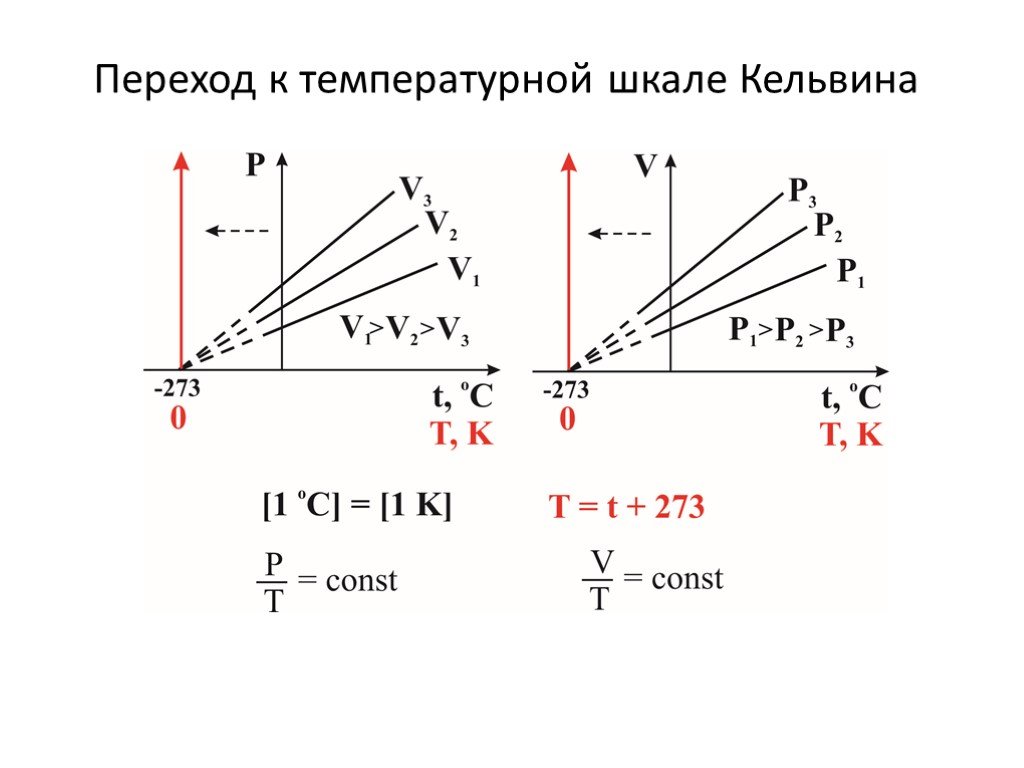
Слайд 20Переход к температурной шкале Кельвина
Слайд 21Атомная единица массы. Количество вещества. Число Авогадро. Молярная масса.
Атомная единица массы (а.е.м.) – mед – единица массы, равная 1/12 массы изотопа углерода С12.
mед = 1,66·1027 кг
Количество вещества, в котором содержится число молекул, равное числу атомов в 12 г С12 (изотопа углерода) называется молем (в 12 кг – киломолем).
Число молекул в одном моле называется числом Авагадро
NА = 6,02·1023 моль1 = 6,02·1026 кмоль 1
Молярная масса – масса одного моля (µ)
При одинаковых температурах и давлениях все газы содержат в единице объёма одинаковое число молекул. Число молекул, содержащихся в 1 м3 при нормальных условиях, называется числом Лошмидта: NL = р0/kT0 = 2,68·1025 м 3.
Нормальные условия: P0 = 105 Па; Т0 =273 К
Слайд 22Уравнение Клайперона
Объединив уравнения Бойля – Мариотта и Шарля, можно найти уравнение идеального газа:
Слайд 23Универсальная газовая постоянная
;
, где В – постоянная для данной массы газа;
, где R – универсальная газовая постоянная; R = 8,31 Дж/К моль Vмоль = V/ν
- количество молей, где m – масса газа, а μ – молярная масса.

Слайд 24§ 4. Основные положения МКТ
1. Вещество состоит из мельчайших частиц атомов или молекул, находящихся в непрерывном движении. 2. В любом, даже очень маленьком, объеме газа, к которому еще применимы выводы МКТ, число молекул очень велико. 3. При отсутствии внешних сил молекулы газа распределяются равномерно по всему объему, предоставленного газу. 4. Направления движения молекул распределены хаотично, значения скоростей изменяются в широких пределах. 5. Соударение молекул друг с другом и со стенками сосуда абсолютно упругие. 6. Размеры молекул малы по сравнению с расстоянием между ними. 7. Молекулы взаимодействуют друг с другом только в момент непосредственного «соударения». В остальное время силами взаимодействия можно пренебречь. 8. Собственный объем молекул газа мал по сравнению с объемом сосуда, предоставленного газу.

Слайд 25§ 5. Основное уравнение МКТ
У реальных газов молекулы обладают конечными размерами и взаимодействуют друг с другом с силами, быстро убывающими с увеличением расстояния между молекулами. По мере уменьшения плотности газа собственный объем молекул делается все меньше по сравнению с объемом, занимаемым газом, а средние расстояния между молекулами становятся настолько большими, что силами взаимодействия молекул между собой можно пренебречь. При ударе о стенку сосуда молекула сообщает ей импульс. Каждый элемент поверхности стенки ΔS непрерывно подвергается бомбардировке большим количеством молекул, в результате чего за время Δt получает суммарный импульс Δp1, направленный по нормали к ΔS.

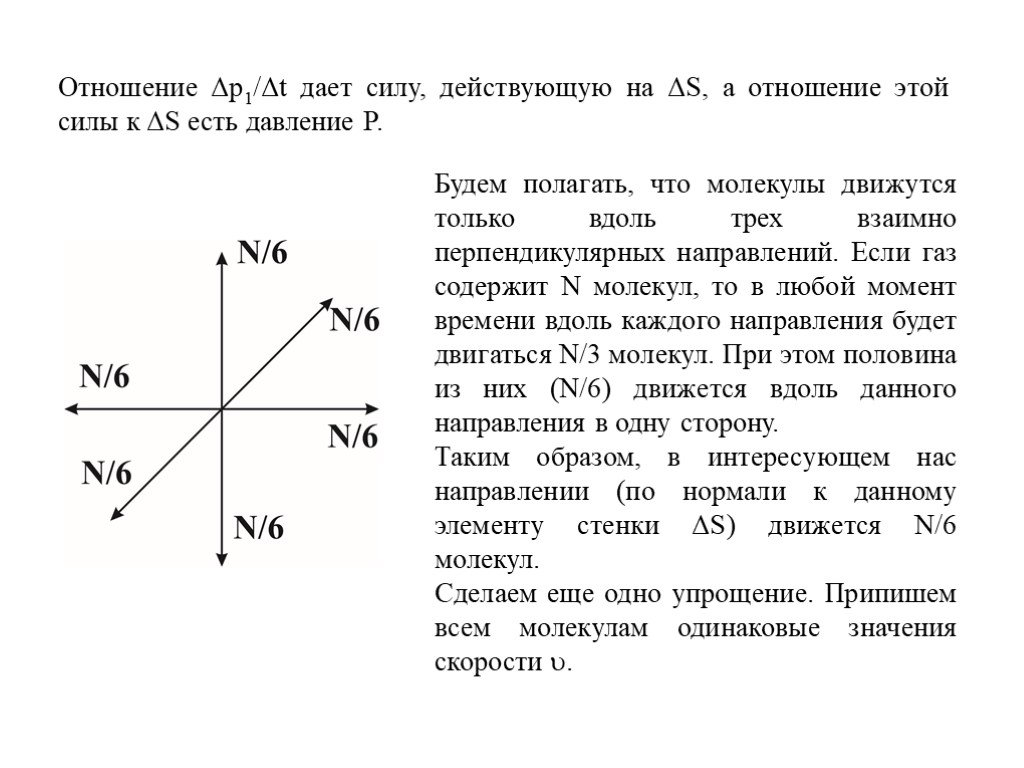
Слайд 26Отношение Δp1/Δt дает силу, действующую на ΔS, а отношение этой силы к ΔS есть давление P.
Будем полагать, что молекулы движутся только вдоль трех взаимно перпендикулярных направлений. Если газ содержит N молекул, то в любой момент времени вдоль каждого направления будет двигаться N/3 молекул. При этом половина из них (N/6) движется вдоль данного направления в одну сторону. Таким образом, в интересующем нас направлении (по нормали к данному элементу стенки ΔS) движется N/6 молекул. Сделаем еще одно упрощение. Припишем всем молекулам одинаковые значения скорости .

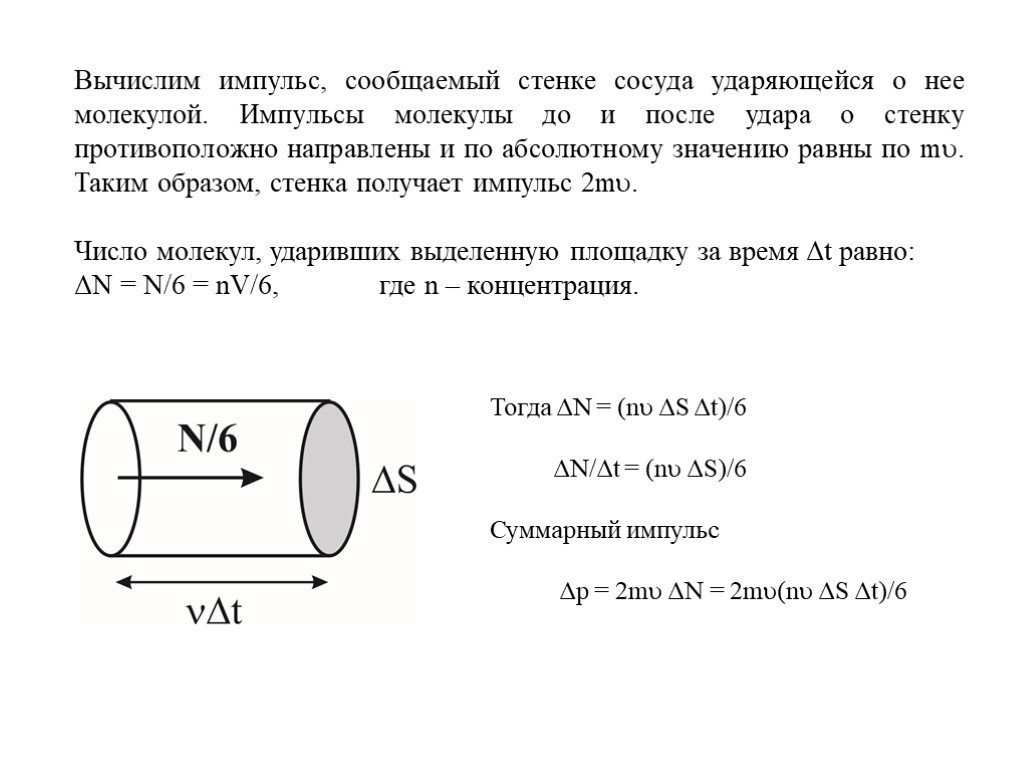
Слайд 27Вычислим импульс, сообщаемый стенке сосуда ударяющейся о нее молекулой. Импульсы молекулы до и после удара о стенку противоположно направлены и по абсолютному значению равны по m. Таким образом, стенка получает импульс 2m. Число молекул, ударивших выделенную площадку за время Δt равно: ΔN = N/6 = nV/6, где n – концентрация.
Тогда ΔN = (n ΔS Δt)/6 ΔN/Δt = (n ΔS)/6 Суммарный импульс Δp = 2m ΔN = 2m(n ΔS Δt)/6
Слайд 28Δp/Δt – сила, действующая на площадку, Δp/(Δt ΔS) – давление газа, оказываемое им на стенку сосуда. Δp/(Δt ΔS) = P = 2m(n ΔS Δt)/(6 ΔS Δt) = (mn2)/3 Учитывая, что (m2)/2 – есть кинетическая энергия поступательного движения молекул, получаем: P = 2/3 nE C учетом распределения молекул по скоростям, возникает необходимость рассмотрения средних значений скоростей, импульсов и энергий. Это уравнение является основным уравнением кинетической теории газов.
Слайд 29Домножим обе части уравнения на молярный объем. PVмоль = 2/3 (n Vмоль)E (n Vмоль) = NА С другой стороны, PVмоль = RT, тогда RT = 2/3 (n Vмоль)E = 2/3 NА E. Следовательно, E = 3/2 T R/NА. R/NА = k – постоянная Больцмана (k = 1,38×10-23 Дж/К). Таким образом, E = 3/2 kT
Слайд 30Из полученного выражения следует важный вывод: абсолютная температура есть величина, пропорциональная средней энергии движения молекул. Этот вывод справедлив не только для газов, но и для вещества в любом агрегатном состоянии. Подставим полученное для энергии выражение в основное уравнение МКТ: P = 2/3 nE = 2/3 n 3/2 kT P = nkT
Слайд 31§ 6. Следствие из основного уравнения
Воспользуемся полученной формулой: P = nkT Поскольку k = R/NА, то P = nTR/NА Концентрация молекул есть отношение количества молекул к объему сосуда, в котором они находятся: n = N/V, тогда P = (N/V)TR/NА = (N/NА) RT/V Откуда следует: PV = (N/NА)RT = νRT или PV/T = (m/μ)RT - уравнение Менделеева-Клайперона.
Слайд 32Если имеется смесь нескольких газов, разные по массе молекулы будут иметь различную скорость, но средняя энергия будет одна и та же. Поскольку P = nkT = (n1 + n2 + n3 + …)kT, где n1, n2, n3, … - обозначают концентрации элементов 1-го, 2-го и т.д. сорта, то P = n1 kT + n2 kT + n3 kT + … Следует заметить, что n1kT – это давление P1, которое было бы в сосуде, если бы в нем находились только молекулы 1-го сорта. Аналогично: n2 kT – это давление P2, n3 kT – это давление P3 и т.д.
Слайд 33Давление, обусловленное молекулами какого-либо одного сорта, при условии, что они присутствуют в сосуде в том количестве, в котором они содержатся в смеси, называется парциальным давлением соответствующей компоненты газовой смеси. P = P1 + P2 + P3 + … Закон Дальтона: Давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.
Слайд 34§ 7. Распределение молекул газа в поле земного тяготения
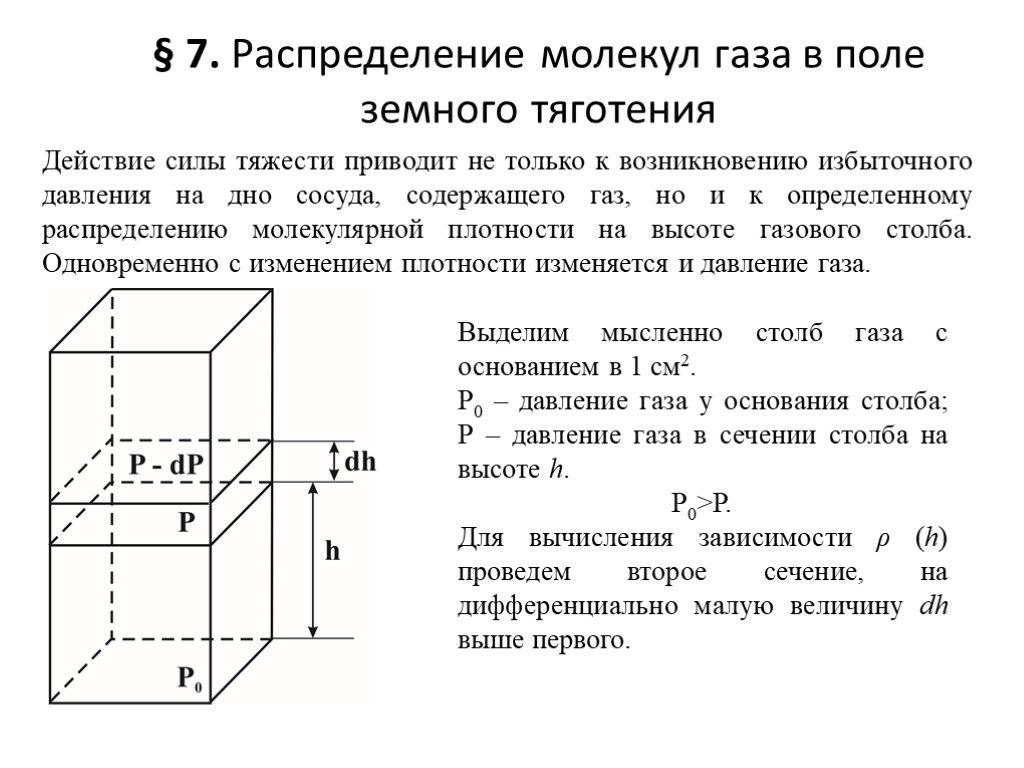
Действие силы тяжести приводит не только к возникновению избыточного давления на дно сосуда, содержащего газ, но и к определенному распределению молекулярной плотности на высоте газового столба. Одновременно с изменением плотности изменяется и давление газа.
Выделим мысленно столб газа с основанием в 1 см2. Р0 – давление газа у основания столба; Р – давление газа в сечении столба на высоте h. Р0>Р. Для вычисления зависимости ρ (h) проведем второе сечение, на дифференциально малую величину dh выше первого.
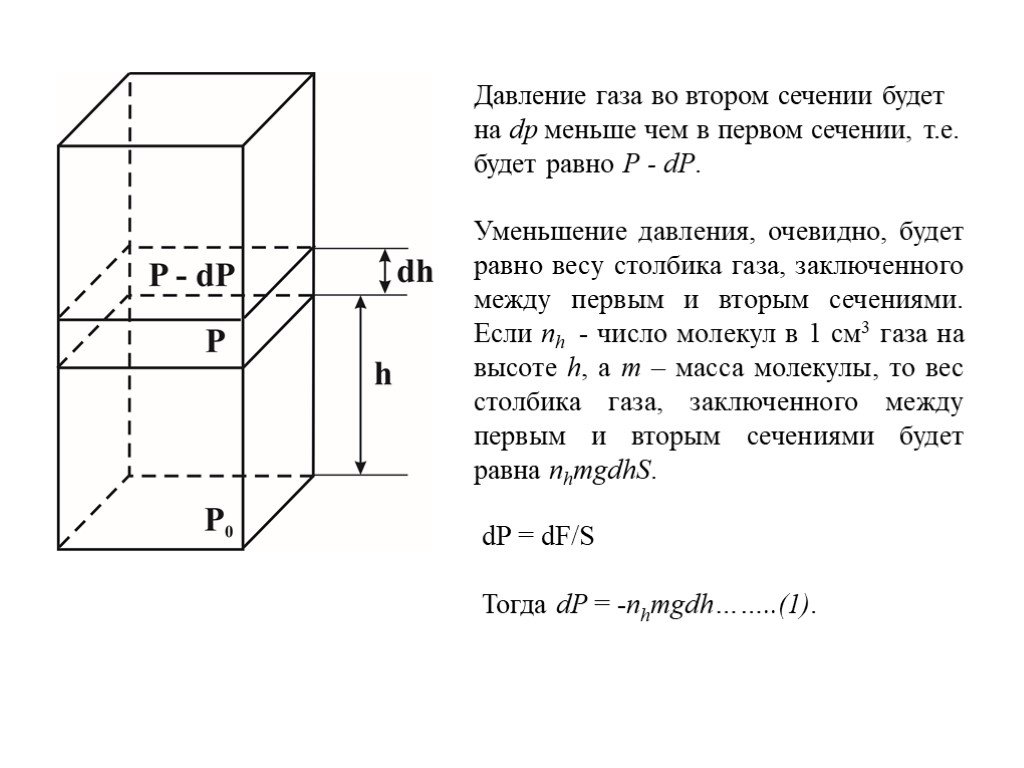
Слайд 35Давление газа во втором сечении будет на dp меньше чем в первом сечении, т.е. будет равно P - dP.
Уменьшение давления, очевидно, будет равно весу столбика газа, заключенного между первым и вторым сечениями. Если nh - число молекул в 1 см3 газа на высоте h, а m – масса молекулы, то вес столбика газа, заключенного между первым и вторым сечениями будет равна nhmgdhS.
dP = dF/S Тогда dP = -nhmgdh……..(1).
Слайд 36Поскольку P = nkT = nhTR/NA , то
Приравняем (1) к (2), получим: -nhmgdh = dnhTR/NA
Интегрируем: ……….(2)
Слайд 37При h = 0 nh = n0 следовательно const = ln n0, тогда
……………..(3)
Поскольку mnh = ρh, а mn0 = ρ0, то
Слайд 38Из (3), домножая на кТ получаем:
Данная формула впервые была получена Лапласом и называется барометрической формулой Лапласа. Если учесть, что μgh – изменение потенциальной энергии одного моля газа при перемещении его от уровня, на котором в 1 см3 содержится n0 частиц до уровня, на котором в 1 см3 – nh частиц, то
Слайд 39§ 8. Распределение Больцмана
Из уравнения
легко получить, что
где m – масса одной молекулы, k – постоянная Больцмана. Отсюда следует, что с понижением температуры число частиц на высотах, отличных от 0, убывает, обращаясь в 0 при Т = 0. При абсолютном нуле все молекулы расположились бы на земной поверхности. При высоких температурах, напротив, n слабо убывает с высотой, так что молекулы оказываются распределенными на высоте почти равномерно. (Причины: притяжение молекул к Земле и тепловое движение).

Слайд 40На разной высоте молекула обладает различным запасом потенциальной энергии: En = mgh. Следовательно, распределение молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. Тогда
где n0 – число молекул в единице объема в том месте, где потенциальная энергия молекулы равна 0, n – число молекул в единице объема в том месте, где потенциальная энергия молекулы равна Еn.
Следовательно, молекулы располагаются с большей плотностью в местах, где их потенциальная энергия меньше. Тогда
где n1 и n2 - количества молекул в единице объема в местах, где их потенциальные энергии соответственно равны Еn1 и Еn2.
Слайд 41как и вытекающая из него формула
справедливы не только в случае потенциального поля сил Земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В соответствии с этим, распределение
называют Распределением Больцмана.
Больцман доказал, что распределение

Слайд 42§ 7. Опыты Перрена. Экспериментальное определение числа Авогадро.
Работы Перрена, сыгравшие исключительную роль в деле утверждения молекулярных представлений, связаны с использованием полученной выше барометрической формулы. Основная идея опытов Перрена сводилась к предположению, что законы МКТ определяют поведение не только атомов и молекул, но и гораздо более крупных частиц, состоящих из многих тысяч молекул.
Предполагается, что средние кинетические энергии очень мелких частиц, совершающих броуновское движение в жидкости, совпадают со средними кинетическими энергиями молекул газа, если температура газа и жидкости одинакова. Точно также распределение по высоте частиц, взвешенных в жидкости, подчиняются тому же закону, что и распределение по высоте молекул газа.
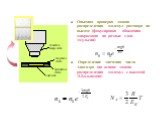
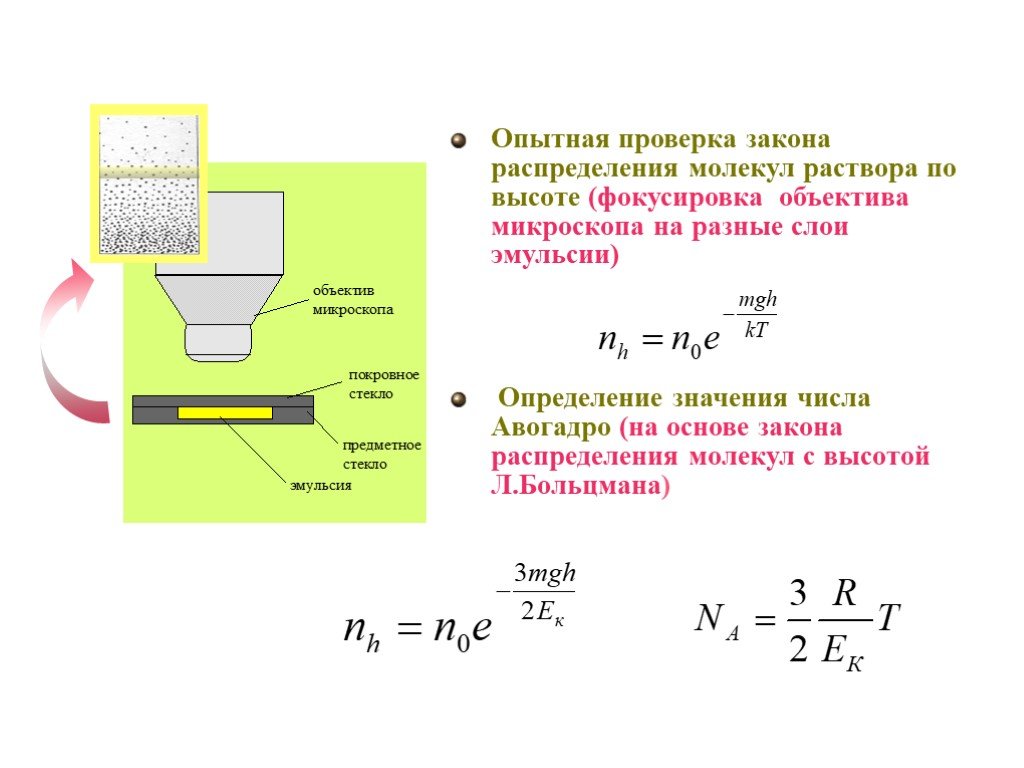
Слайд 43Опытная проверка закона распределения молекул раствора по высоте (фокусировка объектива микроскопа на разные слои эмульсии) Определение значения числа Авогадро (на основе закона распределения молекул с высотой Л.Больцмана)
Слайд 44«…совпадение броуновского движения с требованиями кинетической гипотезы... дает теперь право самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория возведена в ранг научной, прочно обоснованной теории».
О значимости работ Перрена можно судить по следующим высказываниям:
В. Оствальд
«Блестящее определение числа атомов Перреном завершило триумф атомизма ... Атом химиков стал теперь реальностью»
А.Пуанкаре
Таким образом, опыты Перрена являются наиболее ярким экспериментальным подтверждением представлений молекулярно-кинетической теории строения вещества