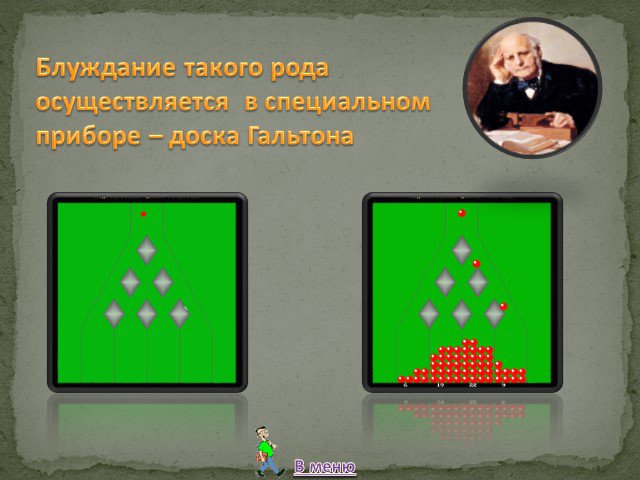
Презентация "Теория вероятностей. Треугольник Паскаля" по математике – проект, доклад
Презентацию на тему "Теория вероятностей. Треугольник Паскаля" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 39 слайд(ов).
Слайды презентации
Список похожих презентаций
Теория вероятностей. Комбинаторика. Комбинаторные методы решения задач
Цель урока: Выработать умение решать задачи на определение классической вероятности с использованием основных формул комбинаторики. Оборудование: ...Теория по молекулярной физике
Литература. Термодинамика. Молекулярная физика – раздел физики, изучающий свойства тел в зависимости от характера движения и взаимодействия частиц, ...Теория относительности Эйнштейна
Задумываясь, какое именно событие все-таки знаменовало зарождение современной науки, я нередко останавливаю свой выбор на одном малоизвестном событии, ...Теория относительности и Альберт Эйнштейн
Альберт Эйнштейн (1879–1955). Кратко об Эйнштейне. Альберт Эйнштейн родился в 1879 г. В 1900 г. окончил Цюрихский политехнический институт. В 1902 ...Теория относительности 1
ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. Постулаты СТО. Кинематика СТО. Современная физика. Классическая физика. СТО. Цель:. Уточнить и углубить ...Теория относительности
Содержание. 1. Рождение теории 2. Принцип относительности 3. Преобразования Галилея 4. Преобразования Лоренца 5. Специальная теория относительности ...Теория электростатической ионизации А. А. Смурова
Введение. Биография А. А. Смурова. Александр Антонович Смуров — русский учёный-физик в области электротехники, специалист по технике высоких напряжений ...Теория электролитической диссоциации
Диссоциация Электролит Неэлектролит Катод, анод Катион, анион Гидратация Диполи Ассоциация Тест Знания. Вещества делятся на:. Электролиты Растворимые ...Закон Паскаля
Цель урока:. Сформулировать закон Паскаля. Опытным путем доказать передачу давления жидкостей и газов во все стороны. Новые понятия. Закон Паскаля, ...Закон Паскаля
ТЕМА УРОКА «Передача давления жидкостями и газами. Закон Паскаля». Перышкин А.В.,. Физика 7 кл. Учебник для общеобразовательных учреждений. §36. Цель ...Закон Паскаля
По горизонтали:. 1. Агрегатное состояние вещества. 2. Воздушная оболочка, окружающая Землю. 3. Агрегатное состояние вещества. 4. Мельчайшая частица ...Закон Паскаля
Сформулировать правила построения изображений в линзах; Научиться строить изображения, даваемые тонкой линзой. Цели урока:. Какие линзы бывают? Линзой ...Давление и закон Паскаля
Наука раскрывает тайны Природы …. Как ответить на шуточный вопрос: «Что легче: тонна железа или тонна пуха?». Почему тяжёлые суда не тонут в воде? ...Давление газов. Закон Паскаля
Сегодня на уроке …. 1 Почему газ давит? 2 От чего зависит давление газа? 3 Как газ передает давление? Повторение Па. Формула расчета давления. Единицы ...Теория света
Физический диктант. 1.Что такое электромагнитная волна? 2.Как доказать, что электромагнитная волна поперечна? 3.При каком условии происходит излучение ...Теория фотоэффекта
Уравнение Эйнштейна для фотоэффекта:. где A – работа выхода электронов из металла. Уравнение получено в предположении, что каждый вылетающий электрон ...Закон Паскаля
Блез Паскаль (1623-1662) — французский математик, физик, религиозный философ и писатель. Сформулировал одну из основных теорем проективной геометрии. ...Теория электролитической диссоциации
Терминология Фарадея. Майкл Фарадей (1791 -1867). Ион Катион Анион Электролит Катод Анод Электролиз Диэлектрическая проницаемость. 1833-1834 гг. Предыстория ...Опыт Паскаля
Блез Паскаль(1623-1662). Французский математик, физик и философ. Первый научный трактат написал в 16 лет. Изобрёл счётную машину. Плодотворно занимался ...Давление газа. Закон Паскаля
Выразите в паскалях давление:. 10 кПа = ? 0,1ГПа = ? 0,025 кПа = ? в углу стоит стол, на столе стопка книг, будет ли оказывать давление стол на все ...Конспекты
Фотоэффект. Теория фотоэффекта
Урок 57. Фотоэффект. Теория фотоэффекта. Цель:. дать понятие явления фотоэффекта; рассмотреть зарождение новой КВАНТОВОЙ ФИЗИКИ и ее влияние ...Передача давления жидкостями и газами. Закон Паскаля
Урок разработан в ТРКМ. Физика 7 класс (35. урок). Тема «Передача давления жидкостями и газами. Закон Паскаля». Задачи:. . Рассмотреть физическое ...Фотоэффект. Теория фотоэффекта
Урок 57. Фотоэффект. Теория фотоэффекта. 11 класс. Разработали: Самойлова Л.И. учитель физики МОКУ «Покровская средняя школа». Никулина О.И. учитель ...Передача давления жидкостями и газами. Закон Паскаля
Новосибирская область, Мошковский район, МБОУ «Сокурская СОШ». Учитель физики Онькова Ольга Владимировна. Урок. в 7 классе. . Тема. «Передача ...Образование электромагнитных волн. Теория Максвелла
Разработка уроков. Образование электромагнитных волн. Теория Максвелла. Тема. . Образование электромагнитных волн. Теория Максвелла. Тип:. сообщение ...Закон Паскаля
Урок по теме: «Закон Паскаля». 7 класс. Цель урока:. познакомить учащихся с законом Паскаля и его практическим применением. . . План урока. ...Закон Паскаля
Урок № 38 7 класс Дата____________. Тема: Закон Паскаля. . Цели:. 1.Введение закона Паскаля. 2.Развитие навыков рассуждения и проведения логического ...Закон Паскаля
Тема. «Закон Паскаля». 7 класс. Цели для ученика:. Общая цель. : совершенствовать знания о давлении твердых тел жидкостей и газов. Образовательные ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Физика
Содержит:39 слайд(ов)
Поделись с друзьями:
Скачать презентацию