Слайд 1Молекулярная физика
Лектор Кунашенко Юрий Петрович ----------------------- д.ф.м.н. профессор
http://portal.main.tpu.ru:7777/SHARED/k/KUNASHENKO
Слайд 3Термодинамика
Молекулярная физика – раздел физики, изучающий свойства тел в зависимости от характера движения и взаимодействия частиц, образующих тело.
Термодинамика анализирует условия и количественные соотношения превращения энергии.
Её первоначальная задача – изучение закономерностей превращения тепла в работу (в тепловых машинах). Основным содержанием современной физической термодинамики является изучение закономерностей тепловой формы движущейся материи и связанных с ней физических явлений.

Слайд 4Совокупность тел, составляющих макроскопическую систему, называется термодинамической системой.
Система может находиться в различных состояниях. Величины, характеризующие состояние системы называются параметрами состояния: давление, температура, объём и так далее.
Любой параметр, имеющий определённое значение для каждого равновесного состояния, является функцией состояния
Равновесной называется такая система, параметры состояния которой одинаковы во всех точках системы и не изменяются со временем (при неизменных внешних условиях).
Процесс – переход из одного равновесного состояния в другое.
Релаксация – возвращение системы в равновесное состояние

Слайд 5Атомная единица массы (а.е.м.) – mед – единица массы, равная 1/12 массы изотопа углерода С12.
mед = 1,66·1027 кг
Количество вещества, в котором содержится число молекул, равное числу атомов в 12 г С12 (изотопа углерода) называется молем (в 12 кг – киломолем).
Число молекул в одном моле называется числом Авагадро
NА = 6,02·1023 моль1 = 6,02·1026 кмоль 1
Молярная масса – масса одного моля (µ)
µ = АmедNА.
При одинаковых температурах и давлениях все газы содержат в единице объёма одинаковое число молекул. Число молекул, содержащихся в 1 м3 при нормальных условиях, называется числом Лошмидта: NL = р0/kT0 = 2,68·1025 м 3.
Нормальные условия: p0 = 105 Па; Т0 =273 К; k – постоянная Больцмана равная 1,38·10 23Дж/К.

Слайд 6Давление. Основное уравнение молекулярно-кинетической теории.
n – концентрация молекул в сосуде; m0 – масса одной молекулы
в единицу времени (1/6) nυ молекул
при абсолютно-упругом ударе m0υx – (m0υx) = 2m0υx
За время dt о стенку, площадью S успеет удариться n = Sυxdt число молекул
Общий импульс, который получит стенка S:
p = dF/dS.
Слайд 7Более точно случайную величину характеризует среднеквадратичная величина.
где Ek – средняя энергия одной молекулы. Это и есть основное уравнение молекулярно-кинетической теории газов.
Иногда за основное уравнение принимают p = nkT. Единицы измерения давления: 1 Па = 1 Н/м2; 1 ат. = 9,8 Н/см2 = 98066 Па 105 Па 1 мм.рт.ст. = 1 тор = 1/760 ат. = 133,3 Па 1 бар = 105 Па; 1 ат. = 0,98 бар.
Слайд 8Температура.
Чем выше температура тела тем больше кинетическая энергия его молекул!
Чтобы связать единицу энергии с градусом, Больцман ввел коэффициент пропорциональности k который впоследствии был назван его именем: k – постоянная Больцмана равная 1,38·1023 Дж·К1
на одну молекулу идеального газа
R – универсальная газовая постоянная
для молярной массы и газа
р = nkT
Слайд 9Изопроцессы идеальных газов.
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
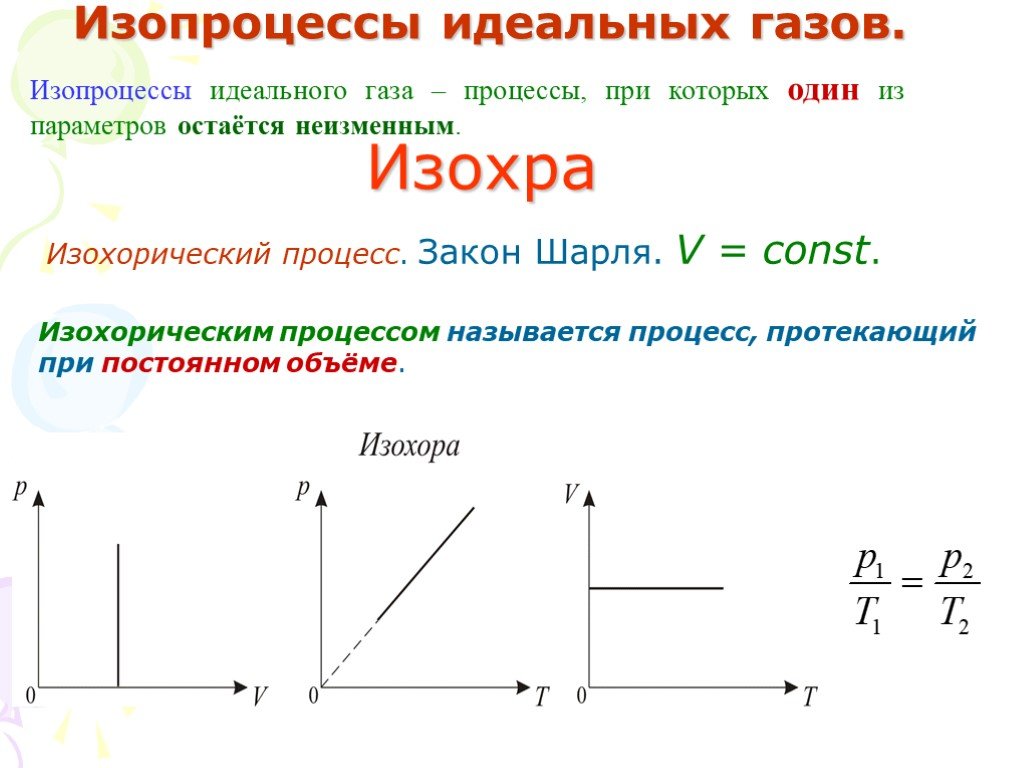
Изохра
Изохорический процесс. Закон Шарля. V = const.
Изохорическим процессом называется процесс, протекающий при постоянном объёме.
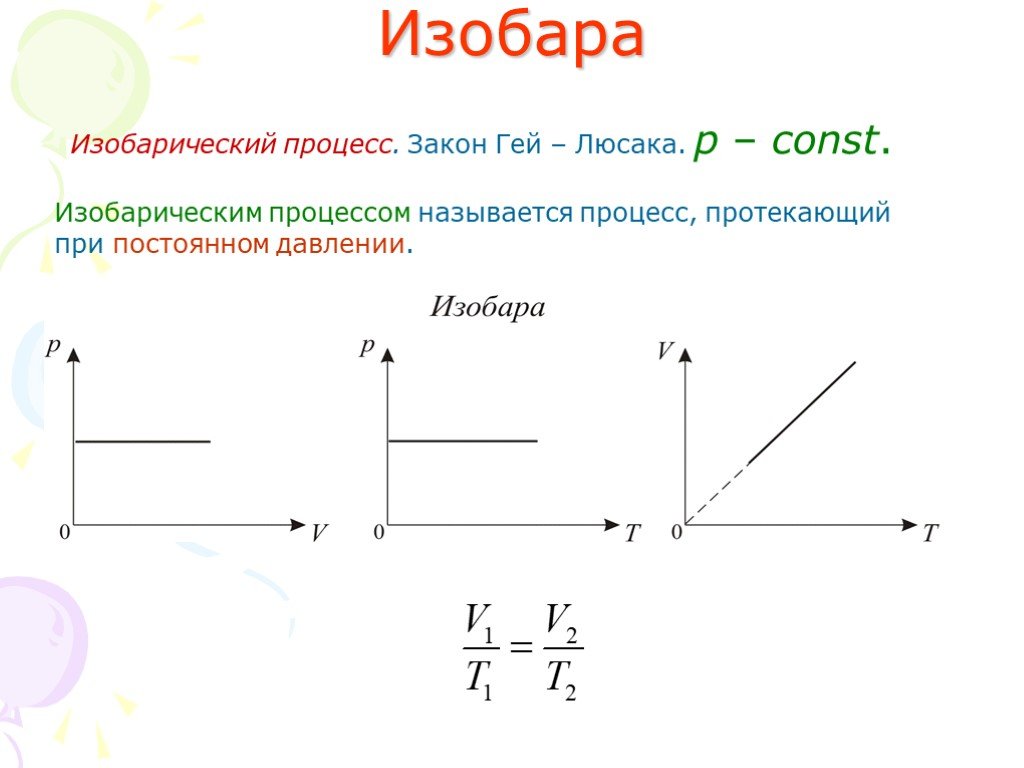
Слайд 10Изобара
Изобарический процесс. Закон Гей – Люсака. р – const.
Изобарическим процессом называется процесс, протекающий при постоянном давлении.
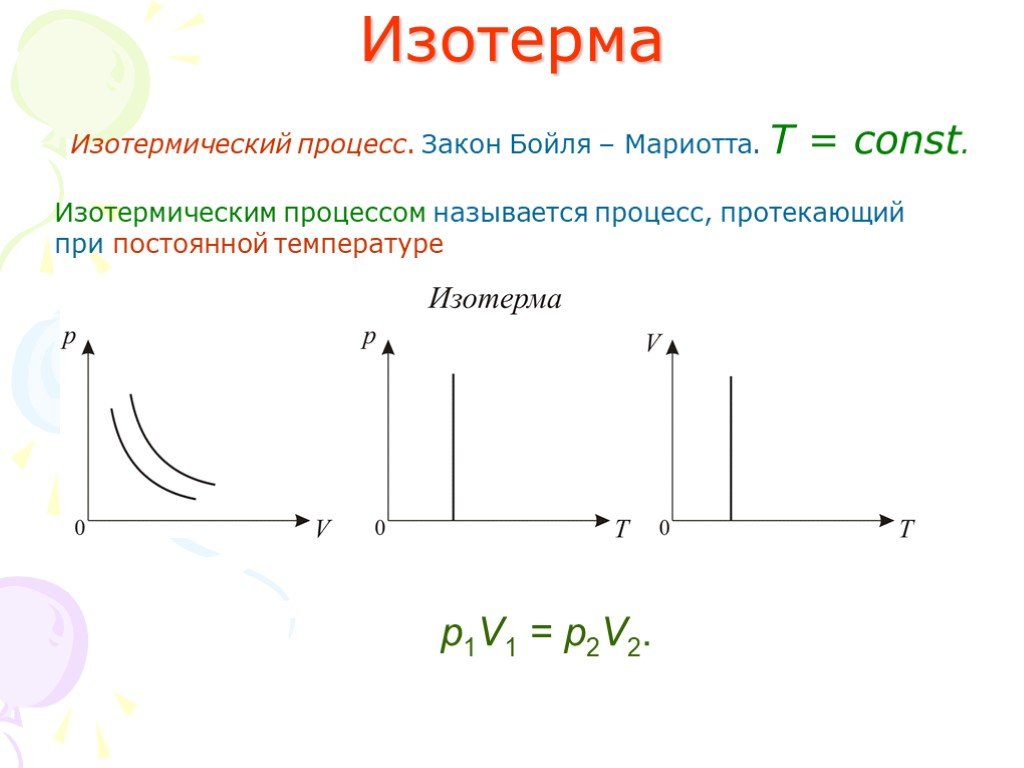
Слайд 11Изотерма
Изотермический процесс. Закон Бойля – Мариотта. T = const.
Изотермическим процессом называется процесс, протекающий при постоянной температуре
р1V1 = р2V2.
Слайд 12Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.
Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA = 6,02·1023 молекул (число Авогадро).
Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений р, входящих в неё газов р = р1 + р2 + ... + рn (р1 – давление, которое оказывал бы определённый газ из смеси, если бы он занимал весь объём)
Слайд 13Объединённый газовый закон (Закон Клапейрона).
Из законов Бойля – Мариотта и Гей – Люссака можно сделать заключение, что для данной массы газа
Слайд 14Уравнение состояния идеального газа - уравнение Менделеева - Клапейрона.
Идеальный газ - газ, молекулы которого пренебрежимо малы, по сравнению расстояния между ними, и не взаимодействуют друг с другом на расстоянии.
МЕНДЕЛЕЕВ объединил известные законы Бойля-Мариотта, Гей – Люсака и Шарля с законом Авогадро.
m – масса газа; μ – молярная масса газа; R – универсальная газовая постоянная; V – объём газа;
– это уравнение Менделеева – Клапейрона для смеси газов
Слайд 15ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Внутренняя энергия. Работа и теплота.
под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул
Тогда: внутренняя энергия U одного моля идеального газа равна
Обмен механической энергией характеризуется совершенной работой (А), а обмен внутренней энергии – количеством переданного тепла (Q).
Слайд 16U = Q – А
изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы
Q = U + А
количество теплоты, сообщаемой телу идёт на увеличение внутренней энергии и на совершение телом работы
Или
Это есть первое начало термодинамики или закон сохранения энергии в термодинамики.
dQ = dU + dA.
Если U = 0, то согласно первому началу термодинамики А = Q т.е. нельзя построить периодически действующий двигатель, который совершал бы большую работу, чем количество сообщенной ему энергии. Иными словами вечный двигатель первого рода невозможен. Это одна из формулировок первого начала термодинамики.
![Теплоёмкость идеального газа. Уравнение Майера. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус. Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на один градус [Cуд] = Дж/К. молярной Теплоёмкость идеального газа. Уравнение Майера. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус. Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на один градус [Cуд] = Дж/К. молярной](https://prezentacii.org/upload/cloud/19/02/128715/images/thumbs/screen17.jpg)
Слайд 17Теплоёмкость идеального газа. Уравнение Майера.
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус
Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на один градус [Cуд] = Дж/К.
молярной теплоемкостью Сμ количество теплоты необходимое для нагревания 1 кмоля газа на 1 градус
Сμ = Суд μ
молярная масса – масса одного моля:
Μ = А mед NА
где А – атомная масса; mед атомная единица массы; NА число Авогадро; μ (моль) – количество вещества

Слайд 18Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
Если газ нагревать при постоянном объёме СV, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии.
Если нагревать газ при постоянном давлении (Ср) в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу. Следовательно проводимое тепло затрачивается и на нагревание и на совершение работы. Ср > CV.
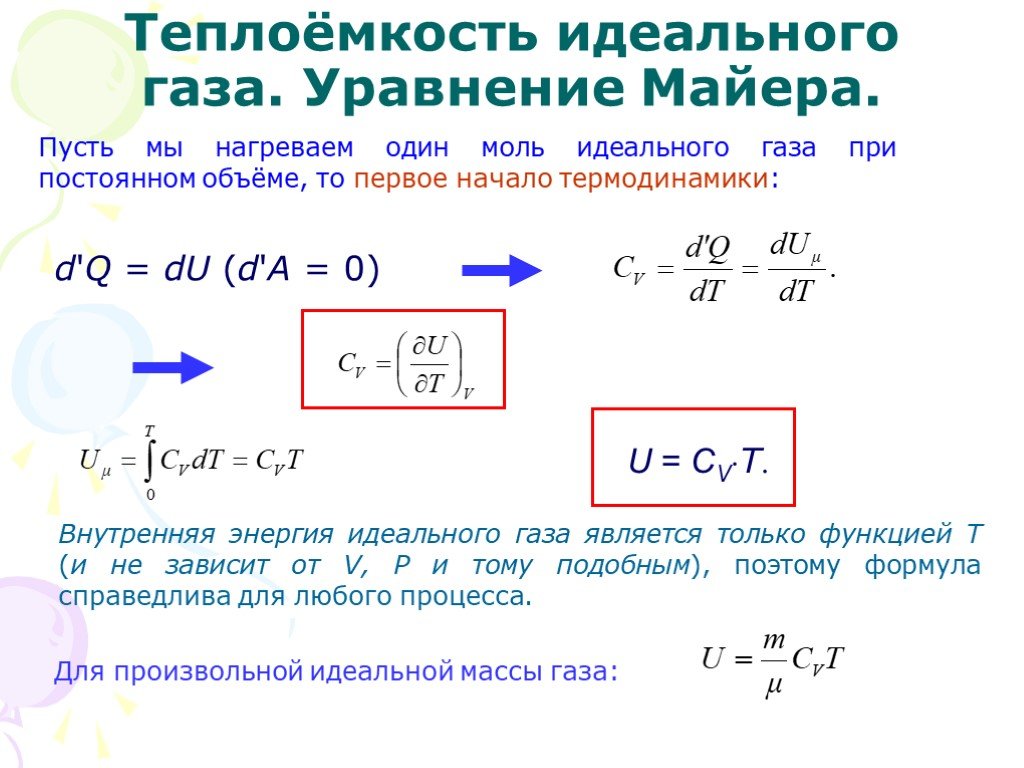
Слайд 19Пусть мы нагреваем один моль идеального газа при постоянном объёме, то первое начало термодинамики:
d'Q = dU (d'А = 0)
Внутренняя энергия идеального газа является только функцией Т (и не зависит от V, Р и тому подобным), поэтому формула справедлива для любого процесса.
U = CVT.
Для произвольной идеальной массы газа:
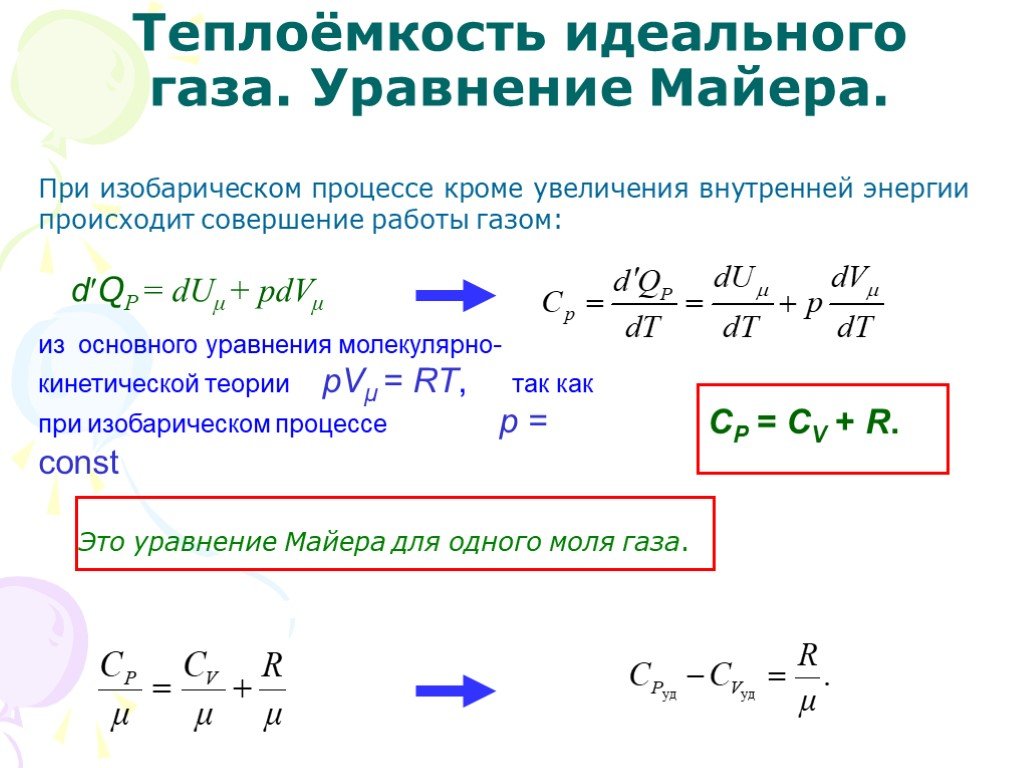
Слайд 20При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы газом:
dQP = dUμ + рdVμ
из основного уравнения молекулярно-кинетической теории рVμ = RT, так как при изобарическом процессе р = const
СР = СV + R.
Это уравнение Майера для одного моля газа.
Слайд 21Теплоёмкости одноатомных газов
Так как энергия одной молекулы идеального газа
, то внутренняя энергия одного моля идеального газа равна
Внутренняя энергия произвольного количества газа:
Её изменение:
Теплоёмкости одноатомных газов СV и СР:
Слайд 22для изобарических процессов можно записать:
dQP = dUμ + RdT (для одного моля).
или
внутренняя энергия
Учитывая:
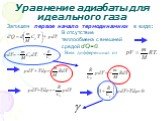
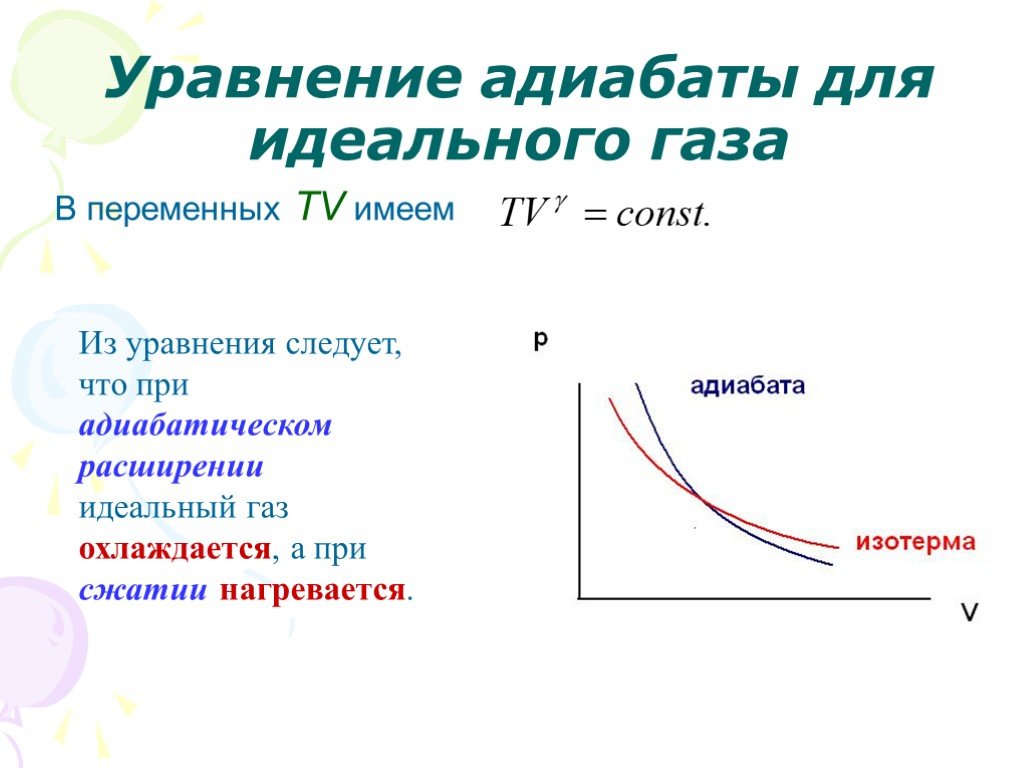
Слайд 23Уравнение адиабаты для идеального газа
P = const – изобарический процесс; V = const - изохорический процесс; T = const – изотермический процесс. При изотермическом процессе pV=const (ур. изотермы). Процесс, протекающий без обмена энергий с внешней средой – адиабатический.
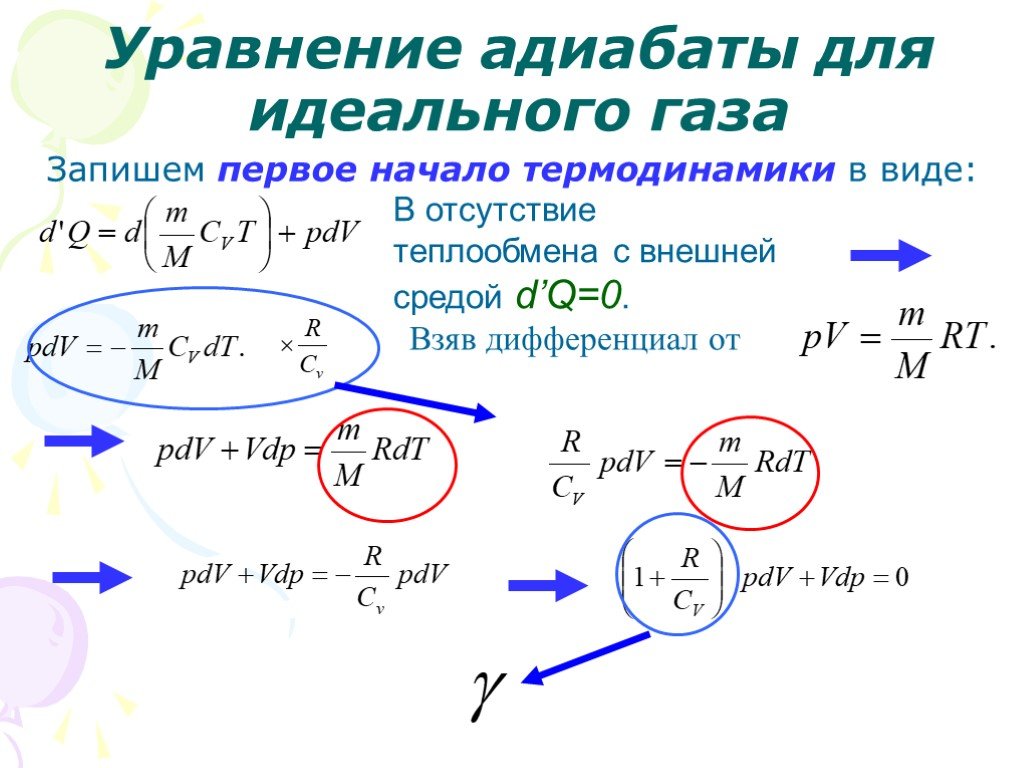
Слайд 24Запишем первое начало термодинамики в виде:
В отсутствие теплообмена с внешней средой d’Q=0.
Взяв дифференциал от
Слайд 25
Слайд 26В переменных TV имеем
Из уравнения следует, что при адиабатическом расширении идеальный газ охлаждается, а при сжатии нагревается.
Слайд 27Политропические процессы.
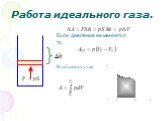
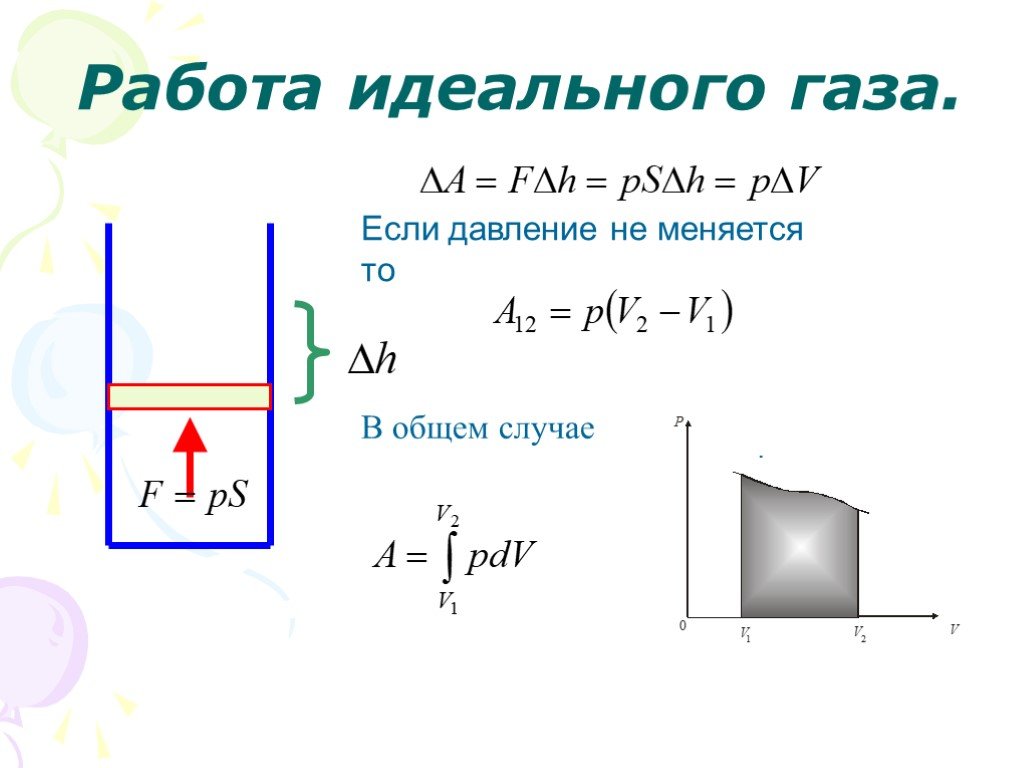
Слайд 28Работа идеального газа.
Если давление не меняется то
В общем случае
Слайд 29Работа А не определяется знанием начального и конечного состояния системы. Её значение зависит от способа («пути») перехода из начального в конечное состояние.
Рассмотрим работу, совершаемую 1 молем идеального газа при изотермическом (T=const) процессе.
Учитывая PV = RT = const, имеем
Слайд 30Уравнение политропы идеального газа
откуда , и работа При Используя
Эта формула справедлива для любого политропического процесса, кроме процесса изотермического (n=1).
Слайд 31Для адиабатического процесса
Слайд 32СТАТИСТИЧЕСКАЯ ФИЗИКА Сведения из теории вероятности
Случайная величина
может иметь значения:
В результате измерений получили:
- относительная частота.
Слайд 33Сведения из теории вероятности
Теорема о сложении вероятностей:
Пусть система характеризуется x и y вероятность которых, равна:
- теорема об умножении вероятностей: вероятность одновременного появления статически независимых событий равна произведению вероятностей этих событий
Среднее значение
Слайд 34Непрерывная случайная величина характеризуется функцией распределения вероятности
Слайд 35Характер теплового движения
В равновесии в газе молекулы движутся хаотически. Изменение скоростей при столкновениях происходит случайным образом. Скорость молекул газа не может быть больше некоторой
Давление газа на стенку
- число молекул в единице объёма,
m - масса молекулы
‹v›- средняя скорость молекул
‹Ek› - средняя кинетическая энергия поступательного движения молекул
Средняя энергия молекул
Слайд 36Так как
Здесь учтена только энергия поступательного движения. Наряду с поступательным движением возможны также вращение молекулы и колебание атомов, входящих в состав молекулы.
Числом степеней свободы механической системы называется число независимых величин, с помощью которых может быть задано положение системы.
Слайд 37Материальная точка задаётся 3-мя координатами; Твердое тело - 3-мя координатами и 2-мя углами и т.д.
Закон равнораспределения – на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная
Слайд 38Для идеального газа
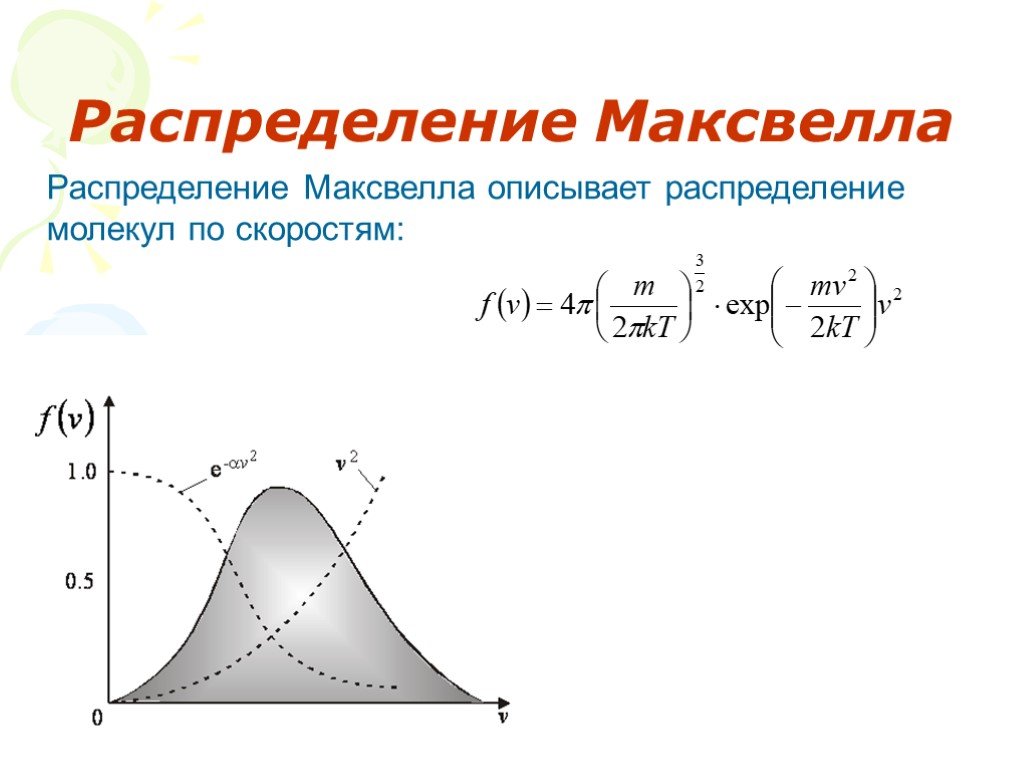
Слайд 39Распределение Максвелла
Распределение Максвелла описывает распределение молекул по скоростям:
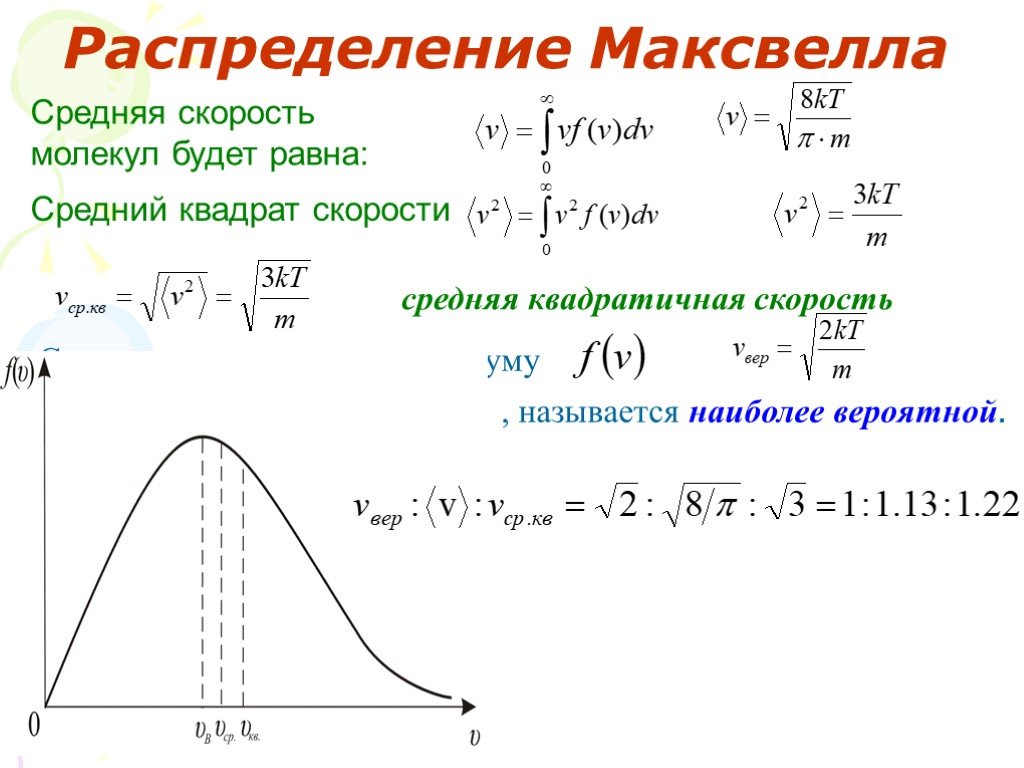
Слайд 40Средняя скорость молекул будет равна:
Средний квадрат скорости
средняя квадратичная скорость
Скорость, отвечающая максимуму
, называется наиболее вероятной.
Слайд 41Для некоторых приложений удобно записать распределение Максвелла как функцию
Это уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры.
Слайд 42Используя очевидное соотношение
Таким образом распределение Максвелла – это распределение молекул по кинетической энергии.
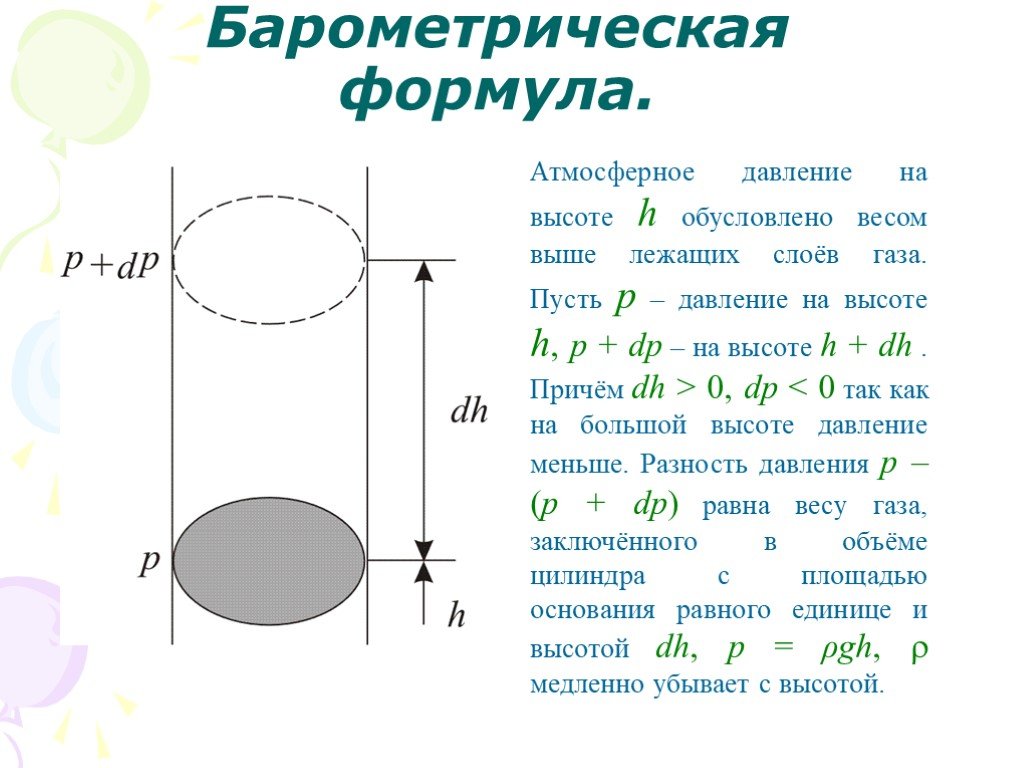
Слайд 43Барометрическая формула.
Атмосферное давление на высоте h обусловлено весом выше лежащих слоёв газа. Пусть p – давление на высоте h, p + dp – на высоте h + dh . Причём dh > 0, dр
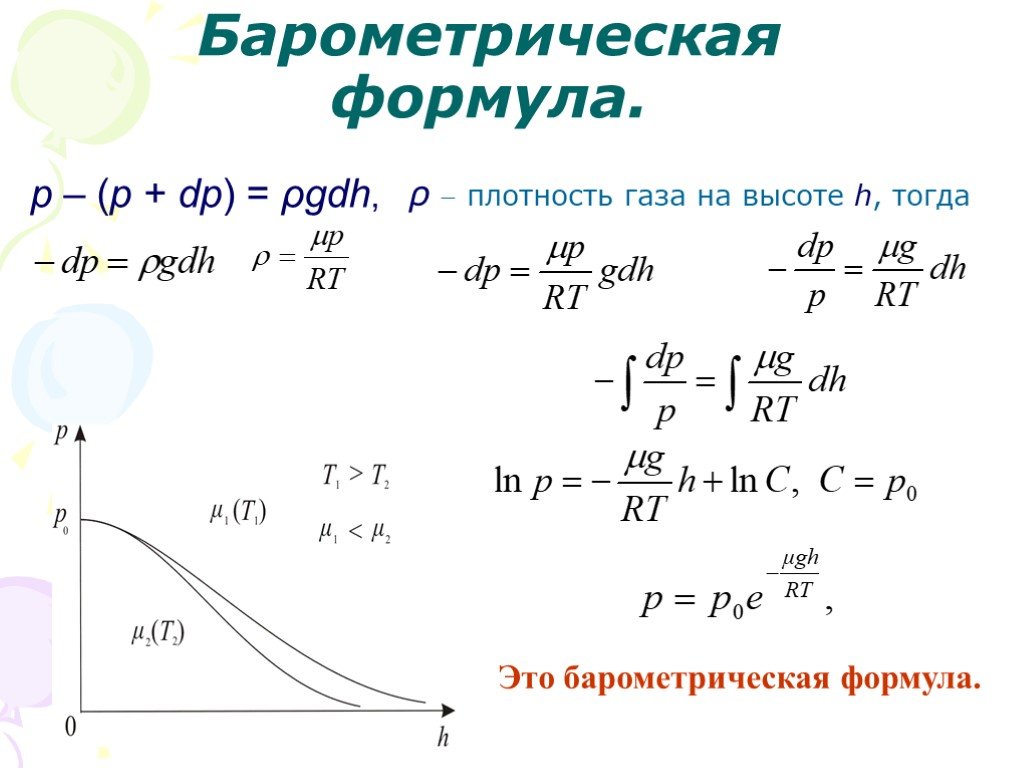
Слайд 44p – (p + dp) = ρgdh,
ρ плотность газа на высоте h, тогда
Это барометрическая формула.
Слайд 45РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА .
Плотность частиц равна
В гравитационном поле Земли
n0 – плотность молекул на уровне моря, p0 – давление уровне моря, h - высота.
В центрифуге
n0 и p0 плотность частиц и давление в центре центрифуги, r – расстояние от центра
Слайд 46Таким образом, молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия
Распределение Максвелла и Больцмана можно объединить в один закон Максвелла – Больцмана
A – нормировочная константа, U – потенциальная mv2/2 – кинетическая, E = U + mv2/2 – полная энергия.
N0 –полное число молекул
Слайд 47Распределение Бозе – Эйнштейна, Ферми – Дирака.
Если у нас имеется термодинамическая система состояния из N частиц, энергии которых могут принимать дискретные значения (W1, W2 ... Wn), то говорят о системе квантовых чисел.
Распределение Бозе – Эйнштейна:
Распределение Ферми – Дирака:
квантовые частицы с целым спином (собственный момент движения) - бозоны (например фотоны)
квантовые частицы с полуцелым спином - фермионы, например: электроны, протоны, нейтроны
Слайд 48Круговые процессы. Тепловые машины.
Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние.
Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – 2) и сжатия (2 – 1) газа.
Работа расширения (определяется площадью фигуры 1a2V2V11) положительна (dV > 0)
Работа сжатия (определяется площадью фигуры 2b1V1V22) отрицательна (dV
Следовательно, работа, совершаемая за цикл, определяется площадью, охватываемой кривой.
Слайд 49Если за цикл совершается положительная работа
то он называется прямым
Если за цикл совершается отрицательная работа
он называется обратным
Слайд 50В результате кругового процесса система возвращается в исходное состояние, полное изменение внутренней энергии газа равно нулю. Первое начало термодинамики для кругового процесса
Q = U + A = A
работа, совершаемая за цикл, равна количеству полученной извне теплоты
система может теплоту как получать, так и отдавать
Q = Q1 – Q2
коэффициент полезного действия
Слайд 51Процесс называют обратимым, если он протекает таким образом, что после окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что в прямом процесс.
никаких изменений в среде, окружающей систему, не произойдет
Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния
Нельзя осуществить необратимый круговой процесс, чтобы нигде в окружающей среде не осталось никаких изменений.
Максимальным КПД обладают машины у которых только обратимые процессы.
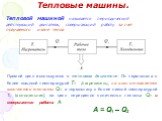
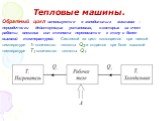
Слайд 52Тепловые машины.
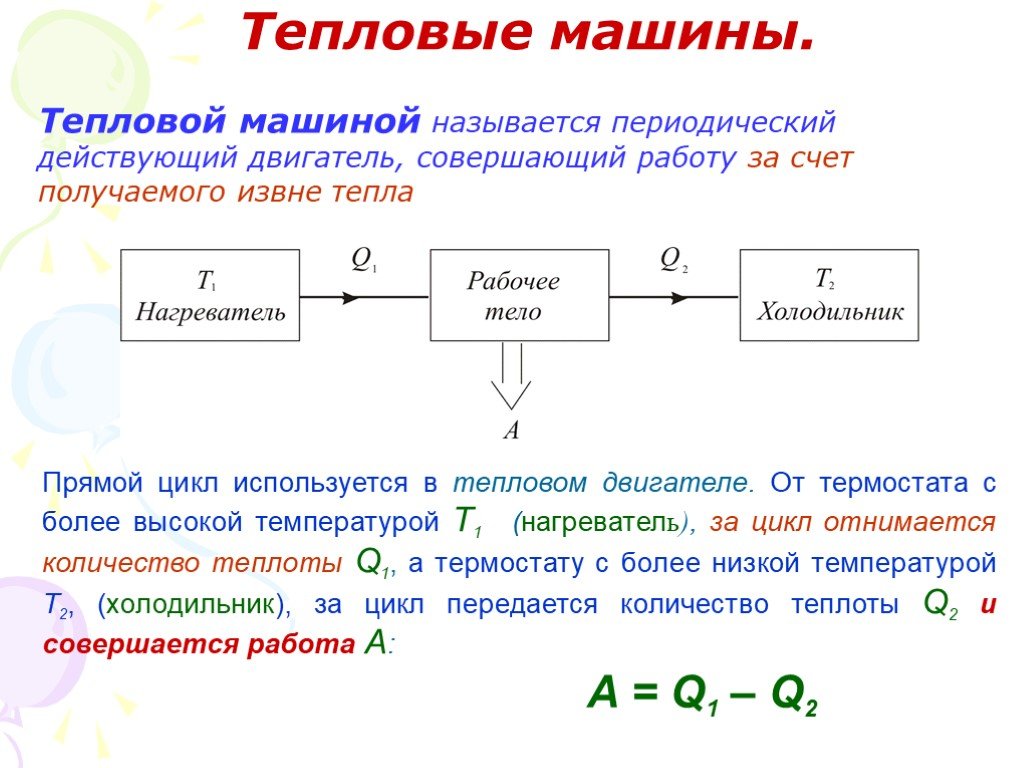
Тепловой машиной называется периодический действующий двигатель, совершающий работу за счет получаемого извне тепла
Прямой цикл используется в тепловом двигателе. От термостата с более высокой температурой Т1 (нагреватель), за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, (холодильник), за цикл передается количество теплоты Q2 и совершается работа A:
A = Q1 – Q2
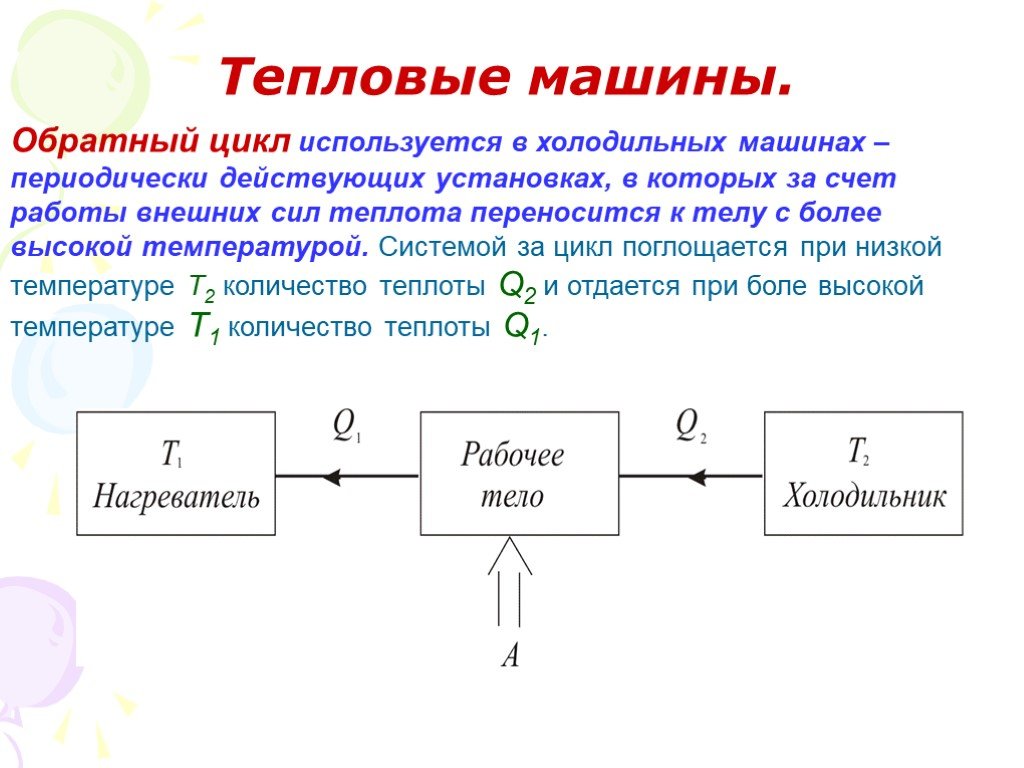
Слайд 53Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. Системой за цикл поглощается при низкой температуре Т2 количество теплоты Q2 и отдается при боле высокой температуре Т1 количество теплоты Q1.
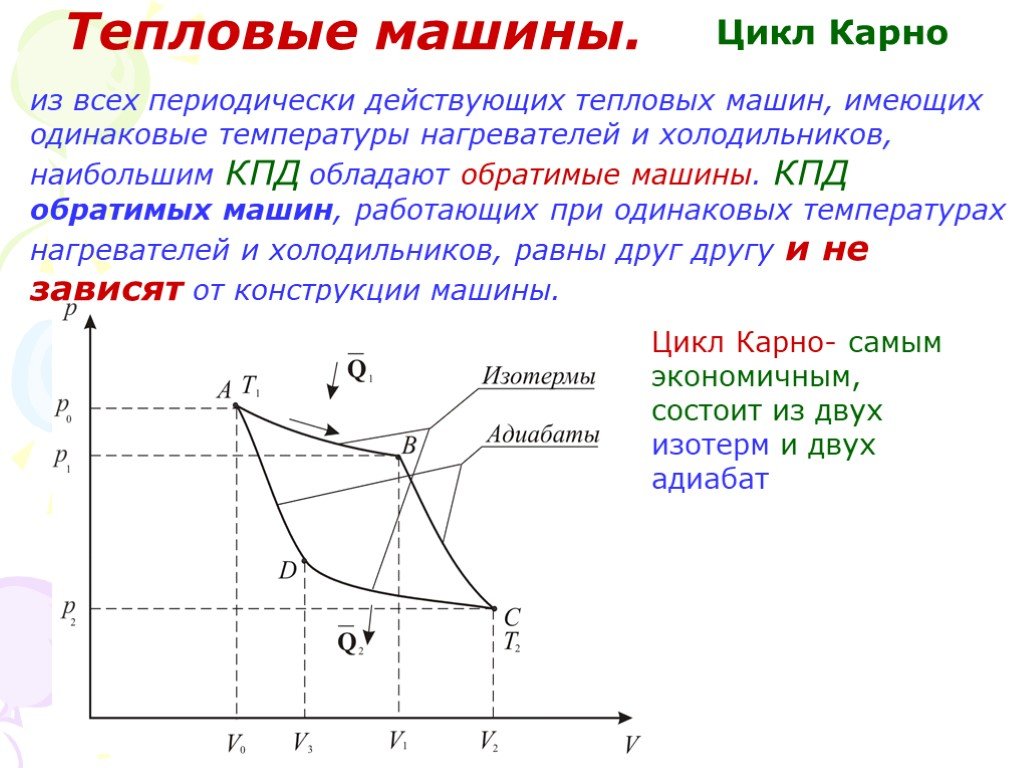
Слайд 54Цикл Карно
из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников, наибольшим КПД обладают обратимые машины. КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машины.
Цикл Карно- самым экономичным, состоит из двух изотерм и двух адиабат
Слайд 55Работа и КПД цикла Карно
Процесс А-В. Положительная работа, совершенная газом при изотермическом расширении одного моля газа от V0 до V1. Тепло, полученное от нагревателя Q1, изотермически расширяется совершая при этом работу А1:
Процесс В-С – адиабатическое расширение. Работа расширения А2 совершается за счет изменения внутренней энергии. Уравнение адиабаты:
Полученная работа на этой стадии
Слайд 56Процесс С-D – изотермическое сжатие. На третьем этапе газ изотермический сжимается V2 до V3. Теплота Q2, отданная газом холодильнику при изотермическом сжатии, равна работе сжатия А3 – это работа совершаемая над газом:
Q2 – тепло, отданное холодильнику
работа сжатия на последнем этапе:
Слайд 57Значит работа совершаемая газом больше работы внешних сил: Работа равна площади ограниченной кривой АВСDА. Из равенств следует:
полезная работа А = Q1 Q2. КПД η равен:
Слайд 58Необратимый цикл. Холодильная машина.
Предположим, что необратимость цикла обусловлена тем, что теплообмен между рабочим телом и источником теплоты (холодильник - “источник”, отрицательной температуры) происходит при конечных разностях температур, т.е. нагреватель, отдавая тепло, охлаждается на ∆T, а холодильник нагревается на ΔТ.
Для необратимого цикла
ηобр > ηнеобр
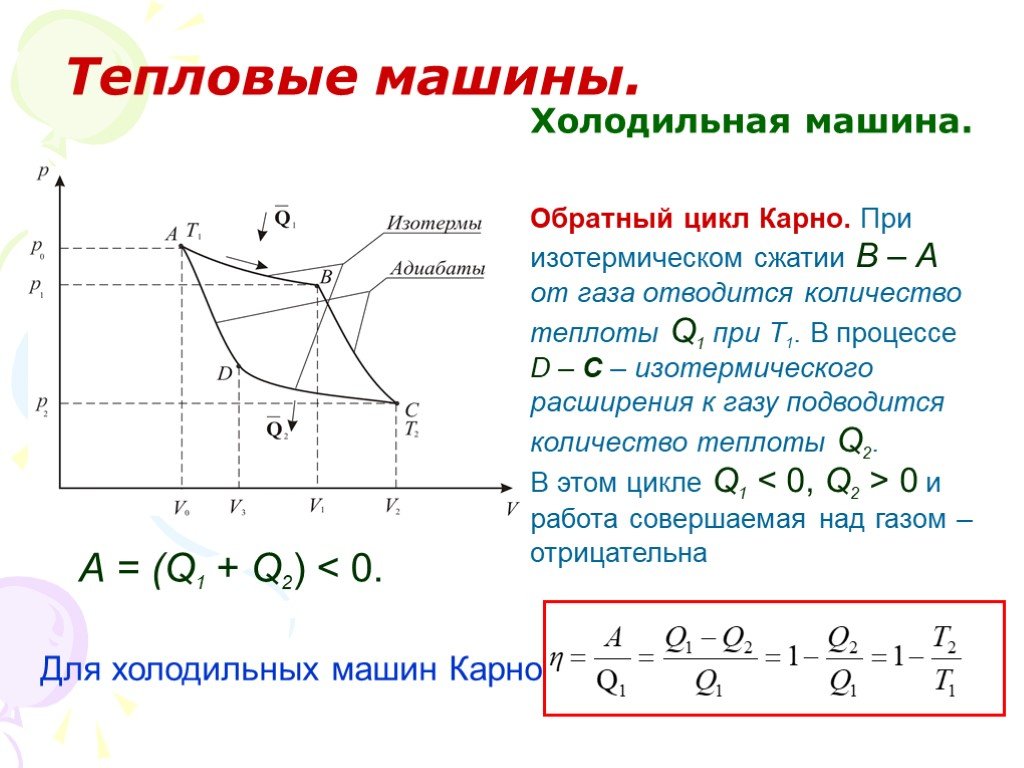
Слайд 59Холодильная машина.
Обратный цикл Карно. При изотермическом сжатии В – А от газа отводится количество теплоты Q1 при Т1. В процессе D – С – изотермического расширения к газу подводится количество теплоты Q2. В этом цикле Q1 0 и работа совершаемая над газом – отрицательна
А = (Q1 + Q2) Для холодильных машин Карно
Слайд 60ЭНТРОПИЯ. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.
Из цикла Карно видно, что равны между собой отношения теплот к температурам, при которых они были получены или отданы:
в изотермическом процессе
Отношение теплоты Q1, в изометрическом процессе, к температуре, при которой происходила передача теплоты, называется приведенной теплотой Q*.
в обратном цикле Карно имеем:
Этот результат справедлив для любого обратимого процесса.
Слайд 61Из равенства нулю интеграла взятого по замкнутому контуру, следует, что
полный дифференциал некоторой функции, которая определяется только состоянием системы и зависит от пути, каким система пришла в это состояние.
Функция состояния, дифференциал которой
, называется – энтропией.
Энтропия обозначается S – это отношение полученной или отданной теплоты к температуре при которой произошла эта отдача.
Для обратимых процессов изменение энтропии
равенство Клаузиуса
Слайд 62Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии:
Последняя формула определяет энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно.
Слайд 63найдем изменения энтропии в процессах идеального газа используя
Слайд 64изменение энтропии S12 идеального газа при переходе его из состояния 1 в состояние 2 зависит от вида перехода 1 2.
изохорического процесса:
изобарического процесса:
p1 = p2
изотермического процесса:
Т1 = Т2
адиабатного процесса:
то
S = const, адиабатный процесс по другому называют – изоэнтропийным процессом
Слайд 65Изменения энтропии при обратимых и необратимых процессах .
Обратимый цикл Карно.
Энтропия (S) – величина аддитивная, т.е.
она равна сумме всех тел входящих в систему.
так как газ возвращается в исходное состояние
так как
Слайд 66Необратимый цикл. ηобр > ηнеобр, т.е.
При любом необратимом процессе в замкнутой системе энтропия возрастает dS > 0. Таким образом для произвольного процесса
где «=» – для обратимого; «>» для необратимого, и для замкнутой системы
Слайд 67Изменения энтропии при обратимых и необратимых процессах . ЭНТРОПИЯ. Второе начало термодинамики.
Второе начало термодинамики.
A = Q1 – Q2.
Работа теплового двигателя.
Чтобы кпд теплового двигателя был = 1, должно быть выполнено условие Q2 = 0
вечный двигатель Второго рода
Невозможно создание вечного двигателя Второго рода подтверждается вторым началом термодинамики:
М. Карно доказал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами.
Слайд 68Невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя в эквивалентной ей работе (формулировка Кельвина). Невозможен двигатель Второго рода (Томсон-Планк). Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему (Клаузиус).
dS 0
Слайд 69При обратном процессе
Клаузиус доказал, что при необратимом процессе
изменение энтропии больше приведенной теплоты, тогда dQ
тогда первое и второе начала термодинамики в объединенной форме будут иметь вид:
Слайд 70Свободная и связанная энергии
в обратимом процессе:
F – разность двух функций состояния, а поэтому и сама является функцией состояния. Ее назвали свободной энергией.
Если тело совершает обратный изометрический процесс, то
dT = 0,
Слайд 71Аизот = F1 – F2 - свободная энергия есть работа, которая могло бы совершить тело в обратном изотермическом процессе или,
свободная энергия – есть максимальная возможная работа, которую может совершить система, запасом внутренней энергии:
U = F + TS
Внутренняя энергия системы равна сумме свободной (F) и связанной энергии (TS).
Связанная энергия – часть внутренней энергии, которая не может быть превращена в работу
Слайд 72При одной и той же температуре, связанная энергия тем больше, чем больше энтропия.
При необратимом процессе энтропия увеличивается, до того пока не прекратятся какие-либо процессы (F = 0). Это произойдет, при достижении замкнутой системы равновесного состояния. Вывести систему из этого равновесного состояния можно затратив энергию из вне.
В термодинамике есть еще понятие
– энергетическая потеря в изолированной системе
Tmin температура окружающей среды.
Слайд 73Статистический смысл энтропии.
Макросостояние – это состояние вещества характеризующее его термодинамические параметры.
Состояние же системы, характеризуемое состоянием каждой входящей в систему молекулы называют – микросостояниями.
Термодинамической вероятностью или статистическим весом макросостояния W называется число микросостояний, которым она может быть осуществлена
Термодинамическая вероятность W максимальна, когда система находится в равновесном состоянии.
В состоянии равновесия энтропия максимальна
Слайд 74S – аддитивная величина.
где S энтропия системы;
сумма энтропий тел, входящих в систему.
Вероятность сложного события
где W1 – первое состояние; W2 – второе состояние.
Поэтому аддитивной величиной является логарифм W:
Поэтому Больцман предложил
Слайд 75Связь между S и W позволяет несколько иначе сформулировать второе начало термодинамики:
Наиболее вероятным изменением энтропии является ее возрастание.
Энтропия – вероятностная статистическая величина.
Энтропия системы – максимальна, при достижении системы (замкнутой) равновесного состояния.
Слайд 76Третье начало термодинамики .
Энтропия любой равновесной системы при абсолютном нуле температуры равна нулю.
Отсюда следует, что при T 0
сходится на нижнем пределе S(0) = const или S(0) = 0,
равенство нулю рассматривается как наиболее вероятное
теорема Нернста
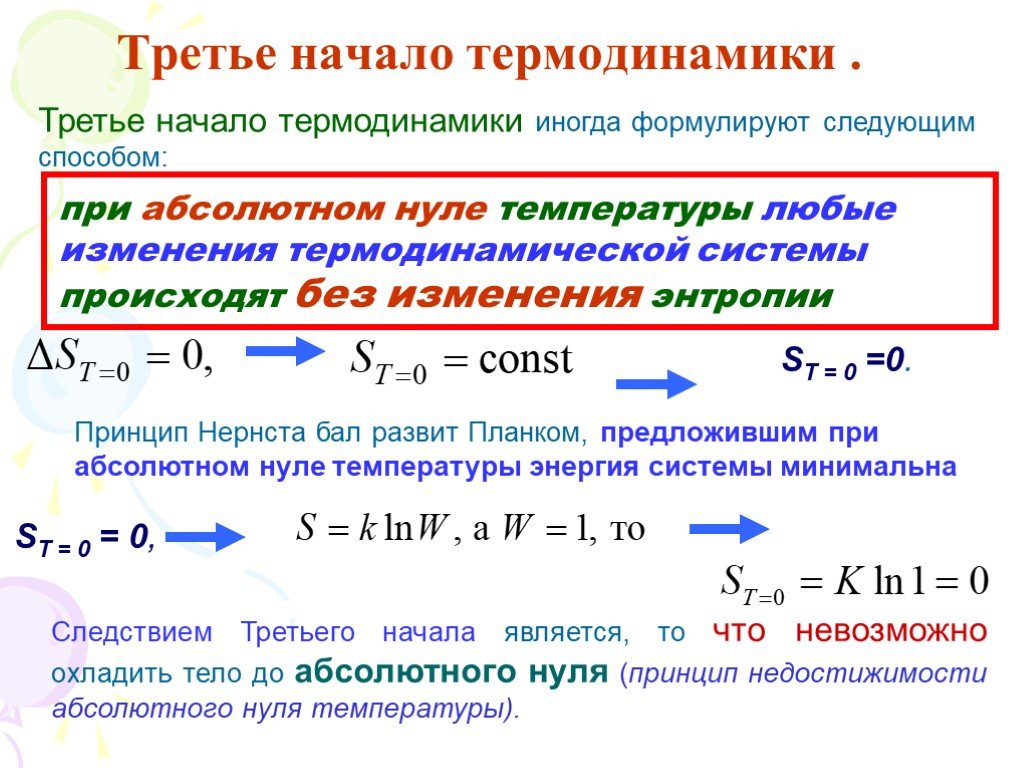
Слайд 77Третье начало термодинамики иногда формулируют следующим способом:
при абсолютном нуле температуры любые изменения термодинамической системы происходят без изменения энтропии
ST = 0 =0.
Принцип Нернста бал развит Планком, предложившим при абсолютном нуле температуры энергия системы минимальна
ST = 0 = 0,
Следствием Третьего начала является, то что невозможно охладить тело до абсолютного нуля (принцип недостижимости абсолютного нуля температуры).
Слайд 78Термодинамические потенциалы.
Термодинамические потенциалы – функции состояния.
Внутренняя энергия
Свободная энергия:
Энтальпия:
Термодинамический потенциал Гиббса:














































































![Теплоёмкость идеального газа. Уравнение Майера. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус. Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на один градус [Cуд] = Дж/К. молярной Теплоёмкость идеального газа. Уравнение Майера. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус. Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на один градус [Cуд] = Дж/К. молярной](https://prezentacii.org/upload/cloud/19/02/128715/images/thumbs/screen17.jpg)