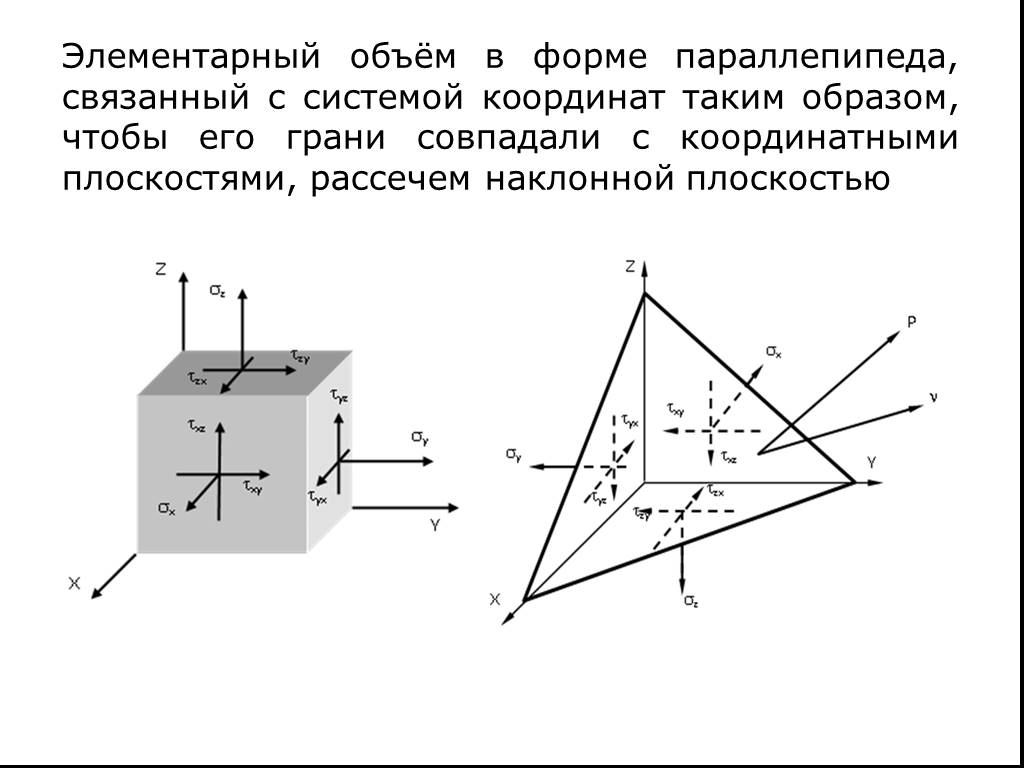
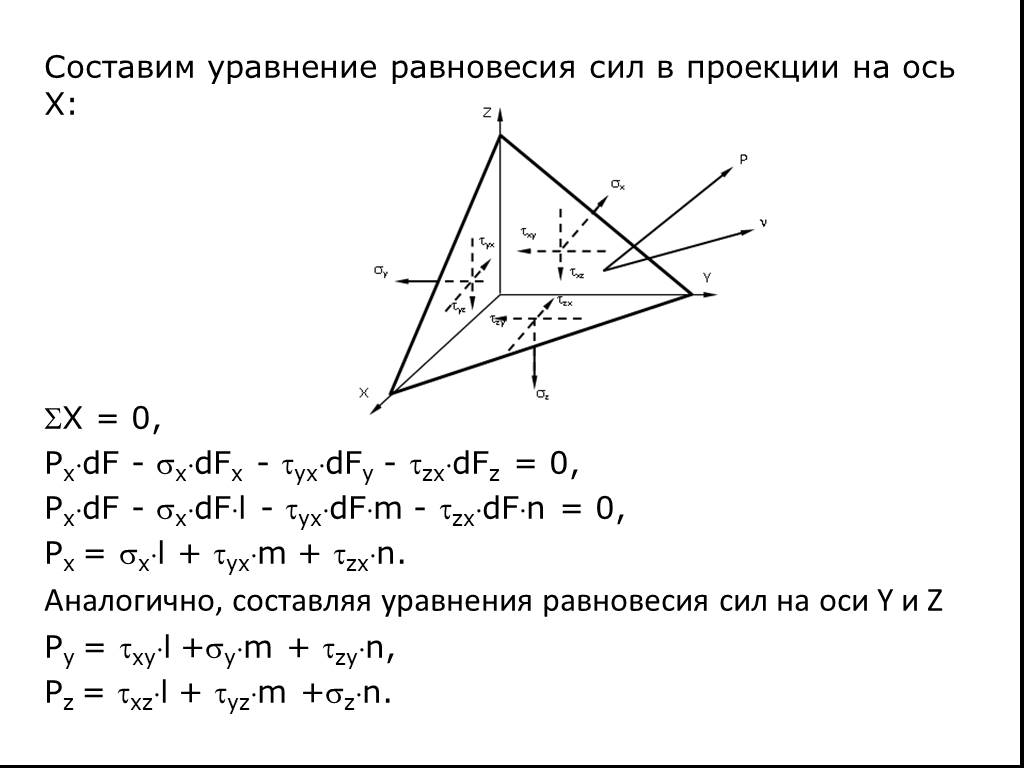
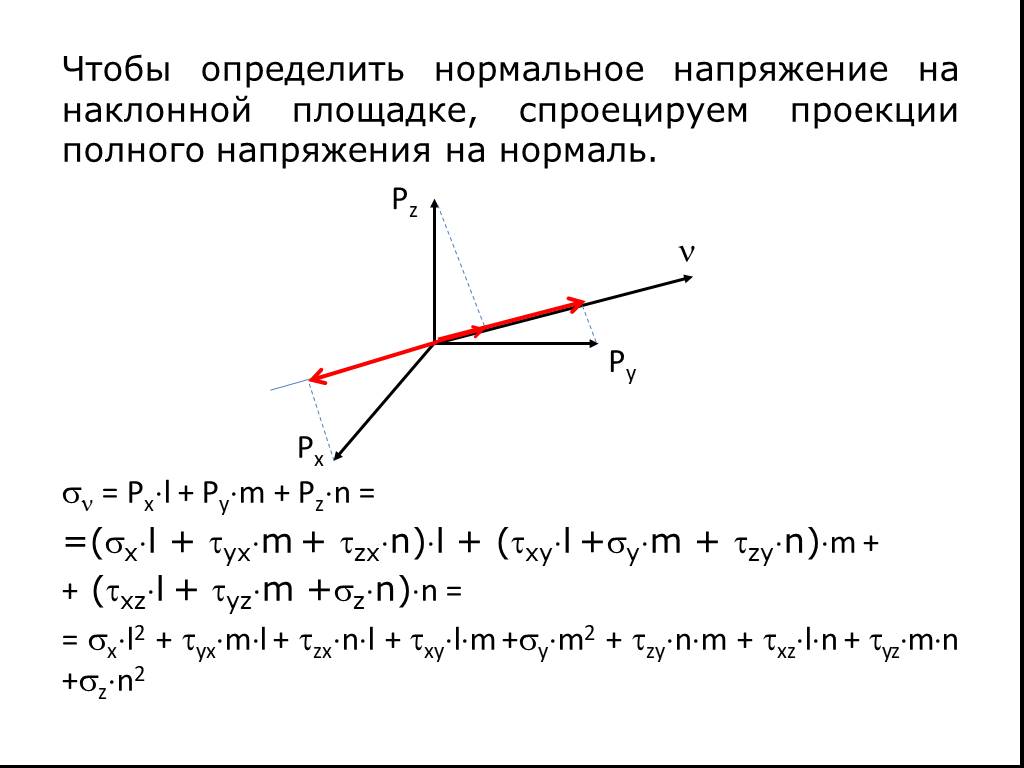
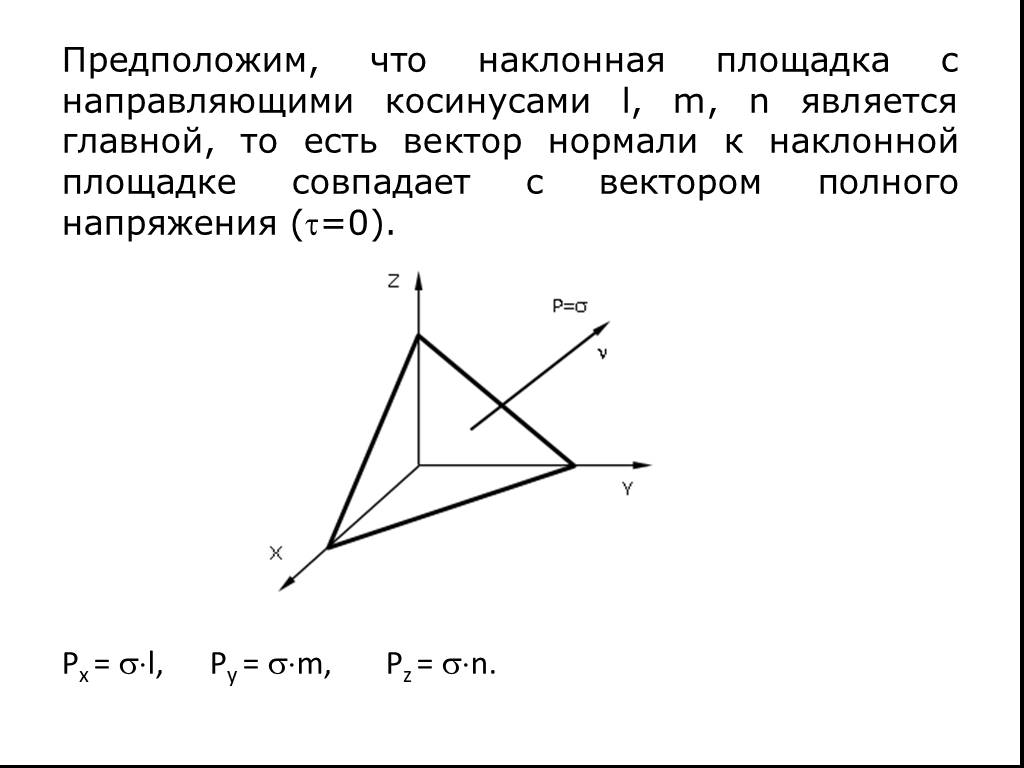
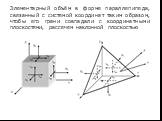
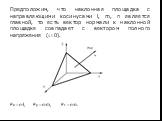
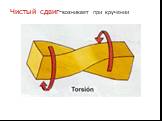
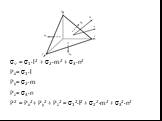
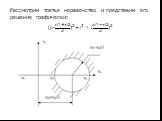
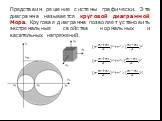
Презентация "Определение напряжений на различных площадках" (8 класс) по физике – проект, доклад
Презентацию на тему "Определение напряжений на различных площадках" (8 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Влияние различных видов звуков на организм человека
Часть I. О ВЛИЯНИИ ПЕСЕН «ТЯЖЕЛОГО МЕТАЛЛА» И РОК-МУЗЫКИ НА САМОЧУСТВИЕ ЧЕЛОВЕКА. «Путь праведного — уклонение от зла: тот бережет душу свою, кто ...Влияние различных участков спектра видимого света на скорость роста растений
Восходишь - все оживает. Заходишь - и все умирает. Ты жизни мерило и первопричина её. ( Гимн Солнцу). Работу выполнил Ученик 8 «Б» класса МОУ СОШ ...Барометр-анероид. Атмосферное давление на различных высотах
Внешний вид. анероид - безжидкостный. Устройство:. 1. металлическая коробочка 2. пружина 3. передаточный механизм 4. стрелка-указатель 5. шкала, деления ...Атмосферное давление на различных высотах
Что такое атмосферное давление? Земля окружена атмосферой - воздушной оболочкой, состоящей из смеси различных газов. Молекулы этих газов, находясь ...Алгоритм решения задач на определение к.п.д. теплового цикла по графику зависимости давления от объема
Задача на определение коэффициента полезного действия по графику зависимости давления от объема. Рассчитайте КПД тепловой машины, использующей в качестве ...Влияние электромагнитных волн на организм человека
Электромагнитные волны – неизбежные спутники бытового комфорта. Они пронизывают пространство вокруг нас и наши тела: источники ЭМ-излучения согревают ...Влияние электромагнитного излучения микроволновой печи на прорастание и рост растений
Гипотеза исследования:. Если электромагнитное излучение отрицательно влияет на организм человека, то оно должно угнетать интенсивность прорастания ..."Мне звезда упала на ладошку"
Мне звезда упала на ладошку. Я ее спросил - Откуда ты? - Дайте мне передохнуть немножко, я с такой летела высоты. А потом добавила сверкая, словно ...Действие электрического тока на тело человека
Виды действия электрического тока. Термическое действие тока проявляется в ожогах отдельных участков тела, нагреве до высокой температуры кровеносных ...Акустический шум и его воздействие на человека
Цель: Исследовать воздействие акустического шума на организм. Задачи: Дать понятие акустики Выявить, как шум воздействует на организм человека? Выяснить, ...Давление на поверхность
Давление твердых тел. I. Повторяем. Назвать указанные физические величины. р. F. S. Какие вы знаете единицы давления? Запишите формулу для давления. ...Воздействие шумов на организм человека
Актуальность исследования. Все процессы в биосфере взаимосвязаны. Человек на протяжении веков стремился не приспособиться к природной среде, а сделать ...Биологические действия радиоактивных излучений на растения…
Мутации растений!!!! По последним исследованиям, это излучение практически безвредно для человека, но очень неблагоприятно действует на растения . ...Биологические действия радиоактивных излучений на животный мир
ДоЗа ИзЛуЧеНиЯ…. Воздействие излучений на живые организмы характеризуется дозой излучения. Поглощенной дозой излучения называется отношение поглощенной ...Антропогенное воздействие на биосферу
Цель:. Выяснить суть влияния человека на биосферу и найти пути выхода из критической ситуации. Нас, как и каждого жителя планеты волнует проблема ...Воздействие радиации на живые организмы
Радиоактивность – отнюдь не новое явление, новизна состоит лишь в том, как люди пытались ее использовать. Радиоактивность, и сопутствующие ей ионизирующие ...Влажность воздуха и его влияние на здоровье человека
Изучить литературы по данной теме. Установить зависимость влажности воздуха и здоровья учащихся. Наблюдать изменение влажности воздуха. Сравнить результаты ...Воздействие радиации на человека
Радиоактивностью называют неустойчивость ядер некоторых атомов, которая проявляется в их способности к самопроизвольному превращению (по научному ...Влияние атмосферного давления и температуры на формирование снежинок
Цель: исследование влияния атмосферного давления и температуры на формирование снежинок, изучение их форм и видов. Задачи:. 1.Узнать, при каких погодных ...Давление в жидкости и газе. Расчёт давления жидкости на дно и стенки сосуда
1.Какую физическую величину называют давлением? Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, ...Конспекты
Барометр – анероид. Атмосферное давление на различных высотах
Тема урока. : Барометр – анероид. Атмосферное давление на различных высотах. Цели:. . Образовательная. :. . 1) изучить работу и устройство барометра-анероида;2) ...Определение КПД при подъёме тела по наклонной плоскости
Тема:. « Определение КПД при подъёме тела по наклонной плоскости». Цели урока:. Образовательная -. . способствовать усвоению учащимися. темы ...Измерение напряжения на различных участках электрической цепи
Тема урока: Лабораторная работа «Измерение напряжения на различных участках электрической цепи». Цели урока:. Предметная:. закрепить ЗУН учащихся ...Определение выталкивающей силы, действующей на погруженное в жидкость тело
Урок, разработанный и проведенный. учителем физики Белой Е. И. в 7 классе. . Тема:. «Определение выталкивающей силы, действующей на погруженное ...Решение задач на расчет давления жидкости на дно и стенки сосуда
Тема урока «Решение задач на расчет давления жидкости на дно и стенки сосуда». 7 КЛАСС (ЗПР). Учитель Пармухина Г.А. Цели:. . . Создать ...Решение задач на применение законов Ньютона
Урок физики в 10 классе по теме: (слайд №1). «Решение задач на применение. законов Ньютона». Цель урока:. Систематизация знаний о законах Ньютона. ...Решение задач на закон Ома для участка цепи
ОТКРЫТЫЙ УРОК по физике. «Решение задач на закон Ома для участка цепи». Учитель: _______ Васильева Зоя Константиновна. Урок по теме. : Решение ...Расчет давления жидкости на дно и стенки сосуда
Учитель:. Смирнова Ирина Владимировна. Класс:. 7. Учебник: «Физика 7 класс», Перышкин А.В. Тема. : Решение задач по теме «Расчет давления жидкости ...Простые механизмы. Рычаг. Равновесие сил на рычаге
Урок. Простые механизмы. Рычаг. Равновесие сил на рычаге. Тип урока. : изучение нового материала. . Цель урока. :. . Обеспечить усвоение ...Определение ускорения свободного падения при помощи маятника
ПЛАН-КОНСПЕКТ УРОКА Тема: Лабораторная работа. . «Определение ускорения свободного падения при помощи маятника». . ФИО. . . Задорожина ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:22 марта 2019
Категория:Физика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию