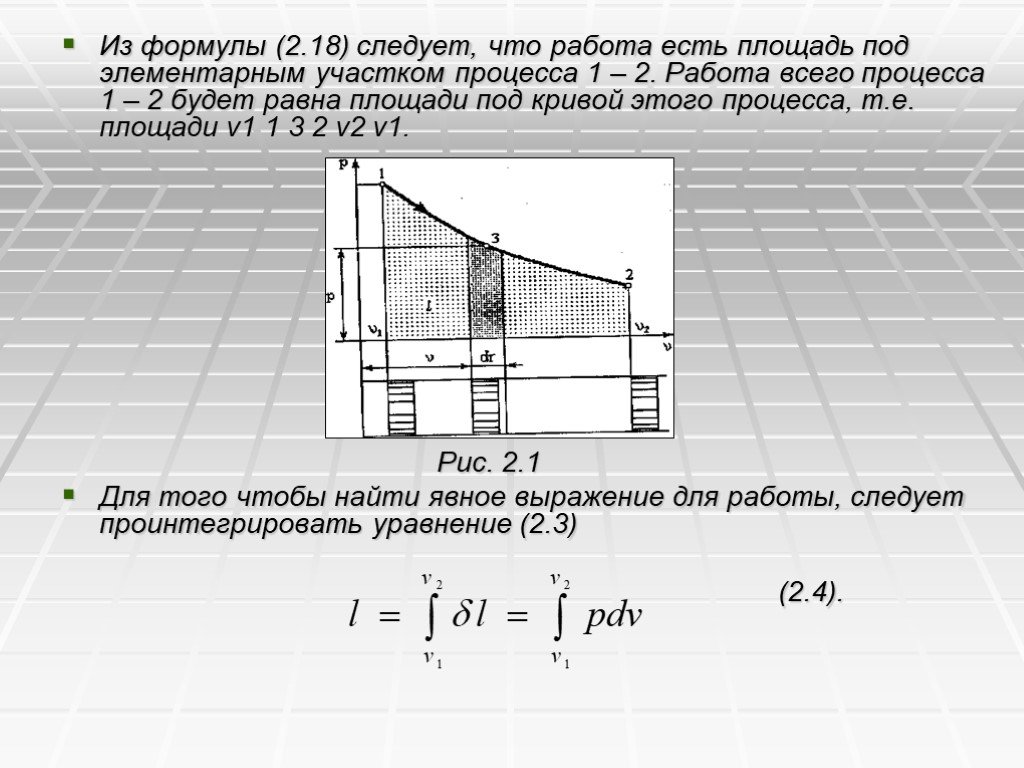
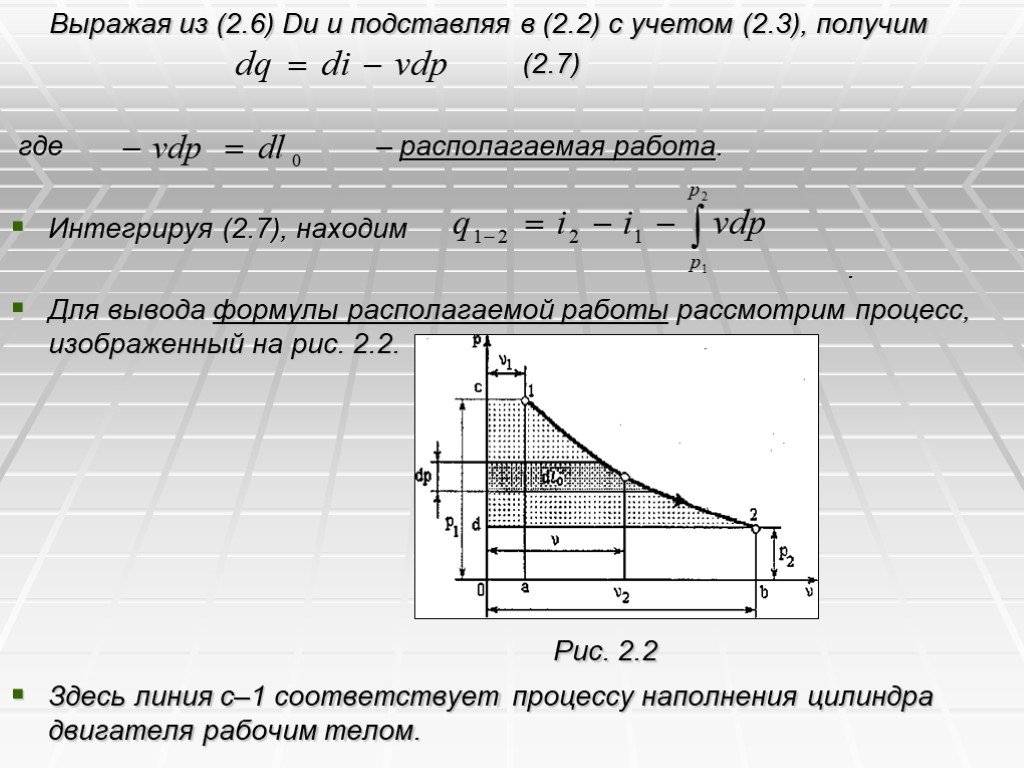
Презентация "Первый закон термодинамики" по физике – проект, доклад

Тема № 2. Первый закон термодинамики

2.1. ЭНЕРГИЯ. ВНУТРЕННЯЯ ЭНЕРГИЯ Энергия является мерой различных форм движения материи. Увеличение или уменьшение энергии системы означает изменение в ней движения в количественном и качественном отношении. Всеобщий закон сохранения и превращения энергии в термодинамике трансформируется в "первое начало" или "первый закон термодинамики". В термодинамике полная энергия макросистемы равна , где Екин – кинетическая энергия системы; Епот – потенциальная энергия системы во внешних силовых полях; U – внутренняя энергия. Кинетическая энергия системы, имеющей массу m и скорость w, определяется по формуле .

Изменение потенциальной энергии системы равно работе, совершаемой над системой при перемещении ее из одного места силового поля в другое. Внутренняя энергия – это энергия, заключенная в системе. Она состоит из кинетической энергии поступательного, вращательного и колебательного движения молекул, потенциальной энергии взаимодействия молекул, энергии внутриатомных и внутриядерных движений частиц и др. Внутренняя энергия является однозначной функцией внутренних параметров состояния (температуры, давления) и состава системы. Ввиду того, что внутренняя энергия является функцией состояния, то ее изменение DU не зависит от формы пути процесса, а определяется лишь ее значениями в конечном и начальном состояниях т.е.

2.2. ТЕПЛОТА И РАБОТА

При протекании термодинамического процесса тела, участвующие в нем, обмениваются между собой энергией. В итоге энергия одних тел возрастает, а других – уменьшается. Передача энергии от одних тел к другим может происходить двумя способами. Первый способ передачи энергии представляет собой передачу энергии в форме теплоты. Такая передача энергии происходит между телами, имеющими различную температуру и приведенными в соприкосновение, либо между телами, находящимися на расстоянии, посредством электромагнитных волн (тепловое излучение). При этом передача энергии происходит от более нагретых к менее нагретым телам. Количество энергии, переданное таким способом, называют количеством теплоты. Теплота, как и любая энергия, измеряется в Джоулях. Произвольное количество принято обозначать буквой Q, а удельное (отнесенное к 1 кг) – q. Подведенная теплота считается положительной, отведенная – отрицательной.

Второй способ передачи энергии называется передачей энергии в форме работы, а количество переданной энергии называется работой. Передача энергии в этом случае происходит при перемещении всего тела или его части в пространстве. Для передачи энергии этим способом тело должно либо двигаться в силовом поле, либо изменять свой объем под действием внешнего давления. Если тело получает энергию в форме работы, то считается, что над этим телом совершается работа. При отдаче телом энергии в форме работы – тело затрачивает работу. Затраченная телом работа считается положительной, а работа, совершенная над телом, – отрицательной. Работа, как и теплота, измеряется в Джоулях. Произвольное количество энергии, переданное в форме работы, обозначается буквой L, а удельное – l. Таким образом, теплота и работа являются двумя качественно и количественно различными формами передачи энергии от одних тел к другим. Работа представляет собой макрофизическую форму передачи энергии, а теплота является совокупностью микрофизических процессов. Передача энергии в виде теплоты происходит на молекулярном уровне без видимого движения тел.

2.3. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Первый закон (первое начало) термодинамики в общем виде представляет собой закон сохранения и превращения энергии. Этот закон налагает строгое условие на все процессы природы, которые при всем их разнообразии ограничены условием сохранения энергии. Дадим несколько формулировок первого закона. 1.Все виды энергии могут взаимно превращаться в строго равных друг другу количествах, т.е. энергия не возникает из ничего и не исчезает, а переходит из одного вида в другой. При переходе механической энергии в теплоту ее отношение к соответствующему количеству теплоты называется термическим эквивалентом работы, который равен J=L/Q=4,1868 Дж/кал, если работа измеряется в Джоулях, а теплота в калориях. Если теплота и работа измеряются в одних единицах, то J=l. Величина, обратная термическому эквиваленту работы, называется механическим эквивалентом теплоты A=l/J=Q/L. 2.Невозможно построить такую периодически действующую машину, с помощью которой можно было бы получить полезную работу без затраты энергии извне, т.е., черпая энергию из ничего. Подобное устройство называется вечным двигателем первого рода, построение и работа которого в соответствии с законом сохранения энергии невозможно.

3. Внутренняя энергия полностью изолированной системы есть величина постоянная. Доказательство этой формулировки будет дано ниже. Некоторое количество теплоты Q. Эта теплота будет затрачена на изменение внутренней энергии DU и на совершение работы L. Тогда для т кг массы тела уравнение эквивалентности будет , (2.1) где Для одного кг массы (т=1) соотношение (2.1) примет вид , где q, Du, l – удельные количества теплоты, изменения внутренней энергии и работы.

Для бесконечно малого процесса (2.2) Соотношение (2.2) представляет собой математическую запись уравнения первого закона термодинамики. Из этого уравнения следует, что теплота, подведенная к рабочему телу, затрачивается на изменение внутренней энергии и на совершение работы. Применим к уравнению (2.2) условия полной изоляции, т.е. dq=0 и dl=0 (система не обменивается с окружающей средой ни теплотой, ни работой). Тогда получим du=0 или u=const, т.к. дифференциал постоянной величины равен нулю. Таким образом, мы доказали, что какие бы процессы не происходили в изолированной системе, ее внутренняя энергия есть величина постоянная. Найдем выражение работы через основные параметры состояния (см. рис. 2.2.). При бесконечно малом перемещении поршня вправо работа 1 кг газа будет , где р – давление в точке 3; S – площадь поперечного сечения поршня; r – перемещение поршня. Так как , то (2.3).

Из формулы (2.18) следует, что работа есть площадь под элементарным участком процесса 1 – 2. Работа всего процесса 1 – 2 будет равна площади под кривой этого процесса, т.е. площади v1 1 3 2 v2 v1. Рис. 2.1 Для того чтобы найти явное выражение для работы, следует проинтегрировать уравнение (2.3) (2.4).

Ввиду того, что работа является функцией процесса, а не функцией состояния, то дифференциал от работы не является полным дифференциалом. В связи с чем некоторые авторы вводят специальное обозначение для бесконечно малого приращения количества работы и количества теплоты , дифференциал которой также не является полным дифференциалом. Будем придерживаться обозначений, принятых в большинстве учебников по термодинамике. С целью упрощения расчетов многих термодинамических процессов У.Гиббсом введена функция I (для m кг массы) и i (для 1 кг), называемая энтальпией. Эта функция вводится по формуле (2.5). Так как и, р и v – функции состояния, то энтальпия i также будет функцией состояния. Так как и, р и v – функции состояния, то энтальпия i также будет функцией состояния. Продифференцируем соотношение (2.5) (2.6)

Выражая из (2.6) Du и подставляя в (2.2) с учетом (2.3), получим (2.7) где – располагаемая работа. Интегрируя (2.7), находим . Для вывода формулы располагаемой работы рассмотрим процесс, изображенный на рис. 2.2. Рис. 2.2 Здесь линия с–1 соответствует процессу наполнения цилиндра двигателя рабочим телом.

Работа, совершаемая внешней средой над рабочим телом, будет равна т.е. площади 0–с–1–а. Эта работа положительна. Линия 1–2 является процессом расширения рабочего тела. Здесь совершается работа расширения Линия 2–d соответствует выталкиванию рабочего тела из цилиндра двигателя. Эта работа затрачивается – она отрицательна и равна . Алгебраическая сумма всех перечисленных выше работ графически равна заштрихованной площади c–l–2–d, которая и представляет располагаемую работу l0 с учетом работы поступления и удаления рабочего тела из машины, т.е. Отсюда (2.8)

Полученное уравнение совпадает с уравнением (2.7). Это уравнение представляет вторую математическую форму записи уравнения первого закона термодинамики. Если в термодинамическом процессе давление остается постоянным, то уравнение (2.7) примет вид . Или для конечного процесса . Таким образом, физический смысл энтальпии состоит в том, что в изобарных процессах изменение энтальпии равно количеству теплоты, поглощенной или отданной системой. В случае отсутствия теплообмена с окружающей средой (адиабатные процессы, dq = 0) уравнение (2.7) будет ,или Следовательно, при dq = 0 располагаемая работа равна разности энтальпий начала и конца процесса. Энтальпия идеального газа, также как и внутренняя энергия, является функцией только температуры и не зависит от объема и давления, т.к. отсутствуют силы взаимодействия между молекулами.

2.4. ТЕПЛОЕМКОСТЬ

Теплоемкостью называется количество теплоты, которое нужно подвести к телу или отнять от него для изменения температуры тела на 1°С. Теплоемкость вычисляется по формуле , Дж/К, (2.10) В зависимости от количественной единицы вещества, к которому подводится теплота, различают: удельную массовую теплоемкость сх [Дж/(кг∙К)]; удельную объемную теплоемкость с'х [Дж/(м3∙К)] и удельную мольную теплоемкость mc [Дж/(моль∙К)]. Удельная теплоемкость сх равна отношению теплоемкости однородного тела к его массе . Таким образом, удельная массовая теплоемкость – это теплоемкость единицы массы вещества (1кг).

Таким образом, удельная массовая теплоемкость – это теплоемкость единицы массы вещества (1кг). Объемной теплоемкостью с'х называется отношение теплоемкости тела к его объему при нормальных физических условиях (p0= 101325 Па, t0 = 0°С). Таким образом, объемная теплоемкость – это теплоемкость количества вещества, занимающего при нормальных физических условиях единицу объема (1 м3). В ряде случаев за единицу количества вещества удобно принимать такое его количество, которое равно молекулярному весу m этого вещества. В этом случае пользуются мольной или молярной теплоемкостью сm где m – молекулярный вес. Теплоемкость зависит от характера процесса. В термодинамике большое значение имеют теплоемкости при постоянном объеме cv и постоянном давлении ср, определяемые по формулам (2.11) (2.12)

Эти теплоемкости находятся в виде отношения количества теплоты, переданной в процессе при постоянном объеме или давлении, к изменению температуры тела. Из уравнения первого закона термодинамики следует, что при постоянном объеме (dv=0) (2.13) Подставляя (2.13) в (2.11), получим (2.14) Учитывая (2.14), (2.13) примет вид При cv=const Изменение внутренней энергии идеального газа в процессе при постоянном объеме равно произведению теплоемкости cv на разность температур тела в конце и начале процесса.

Массовые теплоемкости при постоянных давлении и объеме связаны между собой соотношением, которое называется уравнением Майера , кДж/(кг∙К). (2.15) Из уравнения первого закона термодинамики вида в процессе при постоянном давлении (dp=0) получим (2.16) Подставляя (2.16) в (2.12), находим В термодинамике большоезначение имеет отношение теплоемкостей (2.17) где k – показатель адиабаты (k≈1,67 – для одноатомных, k≈1,4 – для двухатомных, k≈1,29 – для трехатомных газов). Величина k зависит от температуры. Из (2.18) с учетом уравнения Майера сp – cv = R получим (2.18) или для одного моля

Так как с увеличением температуры газа cv увеличивается, то величина k уменьшается, приближаясь к единице, но оставаясь всегда больше ее. Зная величину k, из (2.18) можно определить величину теплоемкости при постоянном объеме Так как , то Так как теплоемкость идеального газа зависит от температуры, а реального газа и от давления, то в технической термодинамике различают истинную и среднюю теплоемкость. Теплоемкость, определяемая отношением элементарного количества теплоты, сообщаемой термодинамической системе к бесконечно малой разности температур, называется истинной теплоемкостью C=dQ/dT. Истинные теплоемкости реальных газов можно выразить в виде суммы двух слагаемых (2.19) где С0 – теплоемкость данного газа в разреженном состоянии (при р→0 или v→∞) и зависит только от температуры. DС – определяет зависимость теплоемкости от давления или удельного объема.

Температурная зависимость теплоемкости приближенно может быть представлена в виде полинома третьей степени от температуры где а0, а1, а2 и а3 – коэффициенты аппроксимации. В практических расчетах при определении количества теплоты обычно применяют так называемые средние теплоемкости. Средней удельной теплоемкостью данного процесса в интервале температур от t1 до t2 называют отношение количества теплоты q1-2, переданного в процессе, к конечной разности температур t2 – t1 (2.20) Количество теплоты, переданное в процессе, находится по формуле (2.21) где с – истинная удельная теплоемкость. Формула (2.20) с учетом (2.21) примет вид

При расчетах тепловых установок приходится иметь дело со смесями газов, а в таблицах приводятся теплоемкости только для отдельных идеальных газов, в связи с чем необходимо уметь определять теплоемкость газовой смеси. Если смесь газов задана массовыми долями, то удельная теплоемкость смеси определяется по формулам ; . где gi, (i=1,2, ...) – массовые доли каждого газа, входящего в состав газовой смеси. Если смесь задана объемными долями ri, (i=1,2, ...), то объемная теплоемкость смеси будет определятьсяпо формулам ; , где c'vi, c'pi – объемные теплоемкости каждого газа.