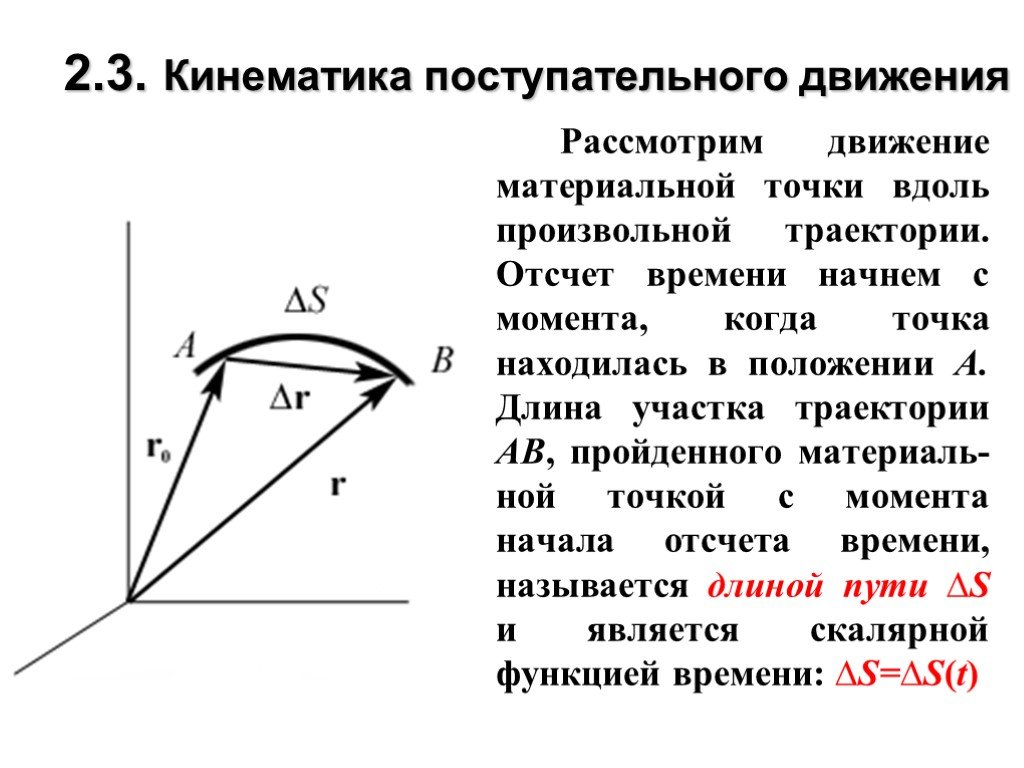
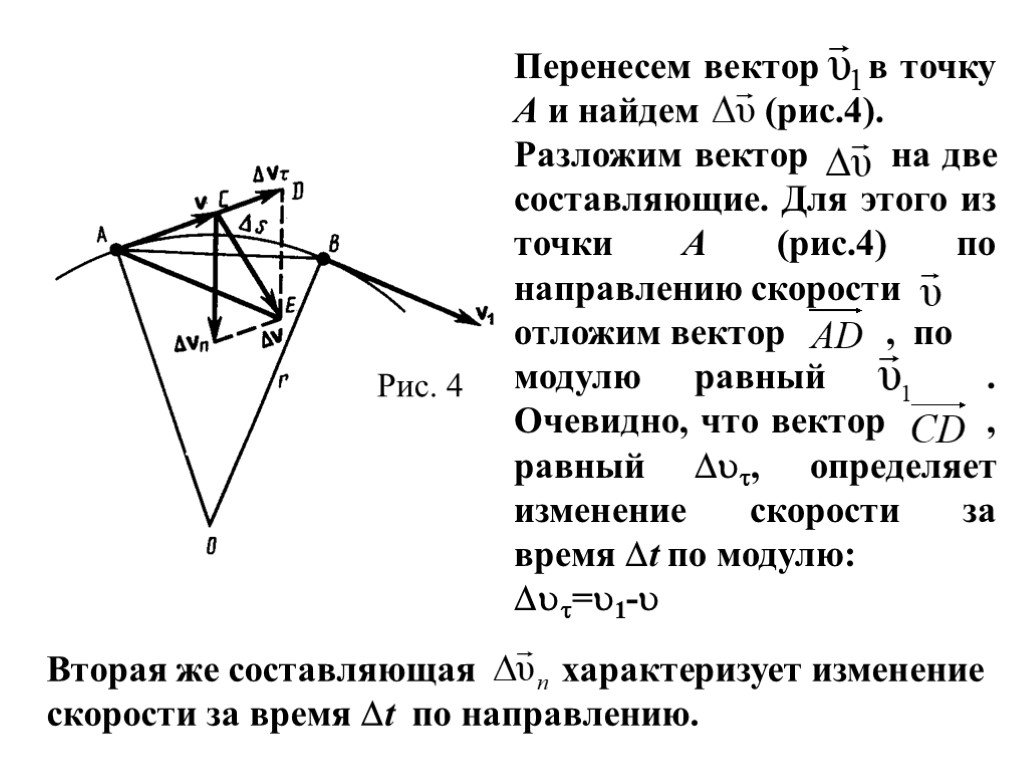
Презентация "Скорость движения" по физике – проект, доклад
Презентацию на тему "Скорость движения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Скорость движения
скорость. Физическая величина, которая определяется отношением пути, пройденного телом за время движения, к тому промежутку времени за который это ...Скорость прямолинейного равноускоренного движения
ВСТАВЬТЕ ПРОПУЩЕННЫЕ СЛОВА В СХЕМЕ. Механическое прямолинейное движение. равномерное неравномерное равноускоренное. С переменным ускорением. ЗАДАНИЕ ...Скорость равномерного прямолинейного движения
Цели урока. Обучающие: Познакомить учащихся с одной из важнейших характеристик механического движения - скоростью, а также с понятиями равномерного ...Скорость равноускоренного прямолинейного движения. График скорости
Расстояние между начальной и конечной точками - это:. путь; перемещение; смещение. Если ускорение равно 2 м/с2, то это:. равномерное движение; равноускоренное ...Скорость равномерного движения
Задание №1 Прочтите два стихотворения Б. Пастернака «Июль» и «По грибы», ответьте на вопросы: 1.Какой процесс, лежащий в основе мироздания и нашего ...Скорость механического движения
Что должны узнать:. Какие важные характеристики механического движения существуют? Какие виды прямолинейного движения существуют? Научиться рассчитывать ...Скорость прямолинейного равноускоренного движения
Цель: сформулировать признаки движения тела с постоянным ускорением. Научить решать графические задачи. Ход урока Проверка домашнего задания. Изучение ...Скорость волны
Гляди в оба! Народная мудрость Рыба анаблепа живет на поверхности воды. Ее глаз разделен на два сектора: верхний видит в воздухе, нижний — в воде. ...Сила трения и безопасность движения школьников
Цель работы:. Выявить влияние силы трения на безопасность движения обучающихся в помещении школы. Задачи: Изучить теоретические основы силы трения; ...Реактивный способ движения
Человечество не останется вечно на Земле, но, в погоне за светом и пространством, сначала робко проникнет за пределы атмосферы, а затем завоюет себе ...Величины, характеризующие колебательные движения
Цель:. Дать школьникам представление о характеристиках колебательного движения: амплитуде, периоде, частоте, фазе колебаний; исследовать зависимость ...Уравнение движения
. . . . . ...Скорость света.
План. Скорость света История измерений скорости света Способы измерения скорости света. Скорость Света – это…. в свободном пространстве (вакууме) ...Изучение механического движения с использованием графиков
Цели:. Образовательные: - Формулирование четких ответов при чтении графиков; - Формулирование четких ответов на качественные задачи; - Применение ...Кинематика прямолинейного движения
Знание становится живым, если оно применяется для достижения определенных целей Ю.М. Орлов. Тип урока: Урок повторения, оценки и коррекции знаний ...Кинематика прямого и поступательного движения
1. Параметры кинематики прямолинейного движения: пройденный путь, перемещение, средняя скорость, мгновенная скорость, ускорение. 2. Прямая задача ...Кинематика криволинейного движения материальной точки
Криволинейное движение. Криволинейное движение тел, которые в данных условиях движения можно принять за материальные точки, часто встречается в повседневной ...Кинематика криволинейного движения
Прямая задача кинематики криволинейного движения. Критерии: угол поворота, угловая скорость, угловое ускорение. Обратная задача кинематики криволинейного ...Исследование баллистического движения
Введение. Баллистика - важная и древняя наука, она применяется в военном деле и в криминалистике. Вместе с этим, она интересна с точки зрения связи ...Конспекты
Скорость движения машин
АВТОМОБИЛИ, скорость, км/ч. ЛиАЗ – 969 М. . 90. . . УАЗ -469. . 100. . . ЗАЗ -968 М. . 118. . . «Ока». . 120. . ...Скорость прямолинейного движения. График скорости
Автор: Бондарева Светлана Александровна, учитель физики МБОУ Сохрановская СОШ Чертковского района Ростовской области. Разработка урока физики в 9 ...Расчет пути и времени движения
Тема «Расчет пути и времени движения». Цели урока:. обучающиеся смогут. . -рассчитывать путь, время и скорость равномерного движения. -строить ...Расчёт пути и времени движения
ОГКУЗ «Детский санаторий г. Грайворон». . . Открытый урок. . по физике. ТЕМА: РАСЧЕТ ПУТИ И. . ВРЕМЕНИ ДВИЖЕНИЯ. Класс 7-й. Учитель:. ...Расчет механического движения с использованием законов динамики
Тема урока –. Расчет механического движения с использованием законов динамики. . Дома. : повторить законы Ньютона, решить задачи № 318 (Л); № ...Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения волн. Свойства механических волн
15.01.2015. Тема : « Распространение колебаний в упругой среде. Волновое движение. Продольные и поперечные волны. Длина волны. Скорость распространения ...Распространение звука. Скорость звука
Тема: Распространение звука. Скорость звука. Цель: Выяснить особенности распространения звука, познакомиться с историй измерения скорости звуковых ...График равномерного прямолинейного движения
Дата. :. Тема урока:. «График равномерного прямолинейного движения. » . 7 Б класс. Цели урока. Познавательные. :. . Научить учащихся пользоваться ...Относительность движения
Урок №. 6. Предмет физика.10кл(ЕМ). Тема:. . Относительность движения. . Цель:. Обучающая :. объяснить понятие об относительности движения. ...Механическое движение. Тело отсчета. Относительность движения
Урок 1 Механическое движение. Тело отсчета. Относительность движения. . . . КГУ «средняя школа имени М.В.Ломоносова». . . Дата: .10.2013. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 февраля 2019
Категория:Физика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию