Конспект урока «Сложение и вычитание двузначных чисел по частям» по математике для 2 класса

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа№ 65 г. Иваново

Конспект открытого урока во 2 - классе

на тему: «Сложение и вычитание двузначных чисел по частям».

Тип документа: конспект

подготовила ГрязноваТатьяна Евгеньевна

учитель начальных классов

Урок 10. Тема: «Сложение и вычитание двузначных чисел по частям».

Тип урока: ОНЗ.

Основные цели:

1) Систематизировать известные способы сложения и вычитания двузначных чисел с целью выбора рационального приёма устных вычислений.

2) Повторить приёмы сложения и вычитания двузначных чисел: по частям, с помощью графических моделей, письменный приём.

3) Систематизировать знания о натуральных числах: что обозначают, что такое натуральный ряд чисел, что 0 не является натуральным числом, …

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, классификация.

Демонстрационный материал:

* карточки для доски:

графические

модели

в столбик

по общему

правилу

по частям

?

* карточка со знаком вопроса: ;

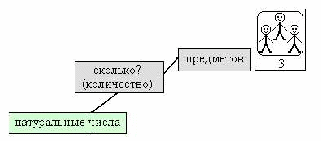
* отдельные карточки для систематизации знаний о натуральных числах: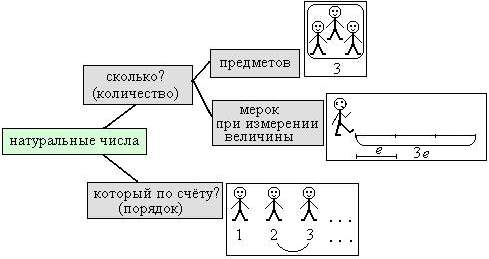

Раздаточный материал:

1) листы с заданием для этапа актуализации:

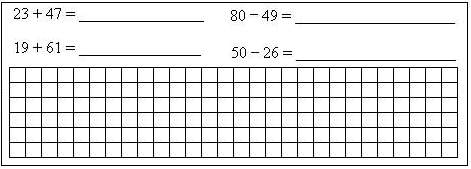
2) листы с заданием для самостоятельной работы:

42 + 38 = ____ 70 – 41 = ____

16 + 24 = ____ 90 – 25 = ____

Ход урока:

1. Мотивация к учебной деятельности:

– Ребята, какой большой теме были посвящены предыдущие уроки? (Сложение и вычитание двузначных чисел.)

– Чем вы занимались на прошлом уроке? (Выясняли, где возникают ошибки, и исправляли их.)

– Вы – молодцы! Многим удалось преодолеть затруднения. И теперь каждый из вас может сказать, что умеет решать примеры в столбик. Но запись «в столбик» – это письменный приём вычислений. Сегодня на уроке мы уделим внимание приёмам устных вычислений. Вы узнаете что-то новенькое. Все знают, как это будет происходить?

– А вначале – потренируем свою наблюдательность и внимание.

2. Актуализация знаний и фиксация затруднения в пробном учебном действии.

Открыть на доске ряд чисел: 43, 34, 25, 16, 7

1) Сложение и вычитание двузначных чисел с использованием графических моделей.

– Повторим все известные вам приёмы вычислений. Начнём с графических моделей.

Повесить на доску карточку с надписью «графические модели».

– А вот какой пример будете решать, вы скажете сами.

– Из чисел ряда составьте пример на сложение двузначного числа с однозначным так, чтобы в сумме было круглое число. (43 + 7.)

– Решите этот пример с помощью графических моделей.

Один ученик у доски решает с объяснением, остальные – в тетрадях.

43 + 7 = 50

(43 – это 4 десятка и 3 единицы, рисую 4 треугольника и 3 точки. Прибавить 7 единиц, рисую 7 точек. Складываем десятки: всего получится 4 десятка, рисуем их в ответе. Складываем единицы: 3 + 7 = 10. 10 единиц – это 1 десяток, заменяем треугольником. 4 десятка да еще 1 десяток, получится 5 десятков или 50.)

2) Запись и решение примеров в столбик.

– Вы получили 50. Выберите из ряда любое двузначное число, которое можно вычесть из 50. (Например, 16.)

– Решите пример, записывая его столбиком.

Повесить на доску карточку с надписью «в столбик».

Один решает у доски с объяснением, остальные – в тетрадях. Эталон этого и других типов примеров остались на рабочем стенде возле доски с прошлых уроков.

(Записываю единицы под единицами, десятки под десятками. В уменьшаемом

0 единиц, поэтому занимаю 1 десяток и дроблю его на 10 единиц. Вычитаю

единицы: 10 – 6 = 4. Пишу 4 под единицами. Уменьшаю количество десятков

уменьшаемого на 1 и вычитаю десятки: 4 – 1 = 3, пишу 3 под десятками. Ответ примера – 34.)

3) Сложение двузначных чисел по общему правилу.

– Составьте из чисел нашего ряда пример на сложение двузначных чисел до круглого. (34 + 16.)

– Запишем пример в строчку и решим его по общему правилу.

Повесить на доску карточку с надписью «по общему правилу».

Один решает у доски с объяснением, остальные – в тетрадях.

34 + 16 = 40 + 10 = 50 (Раскладываю 34 как 30 и 4, а число 16 – как 10 и 6. Складываю

30 4 10 6 десятки: 30 + 10 = 40. Складываю единицы: 4 + 6 = 10;

40 + 10 = 50.)

4) Сложение двузначных чисел по частям.

– Из оставшихся чисел ряда составьте любой пример на сложение двузначных чисел. (43 + 25.)

– Запишите пример в строчку и решим его приёмом «по частям».

Повесить на доску карточку с надписью «по частям».

Один решает у доски с объяснением, остальные – в тетрадях.

43 + 25 = 43 + 20 + 5 = 63 + 5 = 68 (Раскладываю второе слагаемое, как 20 и 5. К 43 сна-

20 5 чала прибавлю 20, получаю 63, потом прибавляю еще 5. Ответ – 68.)

– Итак, какие способы сложения и вычитания двузначных чисел вам известны? (С использованием графических моделей, в столбик, по общему правилу, по частям.)

5) Задание для пробного действия.

– Всё необходимое вы повторили. А теперь задание для пробного действия. Что такое задание для пробного действия? (Это задание, способ выполнения которого мы не знаем.)

Раздать листы с заданием (лицевой стороной вниз):

– Лист с заданием пока не переворачивайте. На этом листе записано 4 известных вам типа примеров. Считать надо будет быстро, поэтому вам необходимо выбрать из известных самый удобный и быстрый способ устного счёта.

– Чем это задание отличается от предыдущих? (В предыдущих заданиях был указан способ вычислений, и не было ограничено время.)

– Что же в этом задании для вас ново? (Нам не приходилось самим выбирать удобный и быстрый способ устных вычислений.)

– Значит, вы не будете выполнять это задание? (Мы попробуем.)

– Итак, за полминуты решите примеры наиболее удобным и быстрым, на ваш взгляд, способом устных вычислений.

– Переворачивайте лист. Начинайте. ( выполняют работу за определенное время)

23 + 47 = 70 80 – 49 = 31

19 + 61 = 80 50 – 26 = 24

– Проверьте. Возьмите зелёную ручку и поставьте знак «+», если все примеры решены верно. Если в примере ошибка, поставьте слева от него «?» и исправьте ответ. Если не успели что-то решить за отведённое время, впишите ответ.

– Поднимите руку, кто что-то не успел решить.

Зафиксировать на доске знаком «–» количество человек, не выполнивших задание полностью: «–» – …чел.

– Кто допустил ошибки?

Зафиксировать на доске знаком «?» количество человек, допустивших ошибки: «?» – …чел.

– Кто все примеры решил верно?

Зафиксировать на доске знаком «+» количество человек, полностью и без ошибок справившихся с заданием: «+» – …чел.

– Давайте выясним, какие способы вы использовали при вычислениях. Поднимите руку, кто использовал графические модели, запись в столбик, общее правило сложения и вычитания, приём «по частям»?

Под карточками с названиями приёмов, расположенных на доске, учитель фиксирует количество человек, которые использовали тот или иной способ.

– Итак, что вы видите? (Что использовали разные способы при решении примеров. Кто-то не успел решить, кто-то допустил ошибки.)

– Значит, чего вы не смогли сделать? Зафиксируйте своё затруднение. (Мы не смогли правильно выбрать удобный способ для устных вычислений.)

– Затруднение вы зафиксировали. Что делать дальше? (Надо остановиться и подумать.)

3. Выявление места и причины затруднения.

– Какое задание вы выполняли? (Надо было выбрать самый удобный способ устных вычислений, чтобы быстро решить примеры.)

– Расскажите, как вы выбирали удобный и быстрый способ устных вычислений? ( Пытались угадать. Выбрали тот, который понятнее …)

– То есть, среди известных вам есть быстрый и удобный способ устных вычислений. Почему же, кто-то не успел, а некоторые при быстром счёте допустили ошибки. (Способ, который выбрали, оказался неудобным для устного счёта. Мы не знаем, какой из известных способов самый удобный, …)

4. Построение проекта выхода из затруднения.

– Какова же цель урока? (Узнать, какой из известных нам способов, самый быстрый и удобный для устных вычислений.)

Учитель открывает на доске запись: «Удобный способ устных вычислений», рядом вешает карточку «?».

– Назовите тему урока. (Удобный способ устных вычислений.)

– Как предлагаете действовать, чтобы из известных вам способов выбрать наиболее удобный для устных вычислений? ( Надо взять один пример, решить его всеми способами и посмотреть, какой из способов короче …)

– Давайте обратимся к результатам вашего пробного действия. Каким способом воспользовалось наименьшее количество человек (или не воспользовался никто)? (Графическими моделями.)

– Почему? (Долго рисовать, выкладывать…)

– Зачем же вам нужны графические модели? (Они помогают увидеть и понять, как происходит сложение и вычитание в разных примерах.)

Учитель снимает с доски карточку «графические модели».

– Какой ещё способ сразу можно исключить? Почему? (В столбик, так как это письменный приём вычислений.)

Учитель снимает с доски карточку «в столбик».

– Что объединяет два оставшихся способа? (Это устные приёмы вычислений.)

– Итак, для выбора наиболее удобного способа устных вычислений у вас осталось два. Назовите их. (По общему правилу, по частям.)

– Как предлагаете действовать дальше, чтобы выяснить, какой из способов короче? (Решить пример обоими способами.)

– Верно, распишем подробно один из примеров обоими способами и посчитаем, где меньше выполняется шагов.

5. Реализация построенного проекта.

– Рассмотрите пример 23 + 47.

По одному у доски с объяснением, остальные – в тетради. Учитель фиксирует знаками (|||…) каждый шаг.

23 + 47 = 60 + 10 = 70

/ \ / \

20 3 40 7 (| | | | |)

23 + 47 = 63 + 7 = 70

/ \

40 7 (| | |)

– Скажите, при применении, какого способа, вы выполнили меньшее количество шагов? (По частям.)

– Значит, какой из способов устных вычислений самый быстрый? (По частям.)

Снять с доски карточку со знаком вопроса.

6. Первичное закрепление с проговариванием во внешней речи.

– Что нужно сделать, чтобы при устном вычислении по частям избежать вычислительных ошибок? (Потренироваться в использовании этого способа.)

– Верно, решите несколько примеров удобным способом.

1) № 2 (а), стр. 18.

– Прочитайте задание.

Задание:

Реши с объяснением:

Решение:

Один у доски с объяснением, остальные – в тетради.

(Раскладываю число 16 на разрядные слагаемые – 10 и 6. К 34 прибавляю 10, получаю 44. К 44

прибавляю 6, получаю 50.)

2) № 3 (а), стр. 18 (задание выполняется в парах с проверкой фронтально).

– Прочитайте задание.

Задание:

Реши с объяснением:

Решение:

(Раскладываю число 49 на разрядные слагаемые – 40 и 9. От 60 отнимаю 40, получаю 20. От 20 отнимаю 9, получаю 11.)

7. Самостоятельная работа с самопроверкой по эталону.

– Что нужно сделать, чтобы убедиться в том, что способ сложения и вычитания по частям действительно удобен и быстр для устных вычислений? (Нужно решить этим способом примеры на время.)

Раздать листки с самостоятельной работой.

42 + 38 = ____ 70 – 41 = ____

16 + 24 = ____ 90 – 25 = ____

– Решите примеры за полминуты.

Для того, чтобы убедить детей в рациональности используемого способа, учитель может немного увеличить время выполнения задания, не говоря об этом детям.

Открыть образец на доске.

42 + 38 = 80 70 – 41 = 29

16 + 24 = 40 90 – 25 = 65

– Проверьте.

– Все ли успели выполнить задание? (Все.)

– Какой вывод можно сделать? (Что способ сложения и вычитания по частям действительно удобен для устных вычислений.)

– У кого возникли затруднения? С чем они связаны? (С вычислительными ошибками.)

– Над чем надо поработать? (Надо тренироваться в счёте.)

– У кого всё получилось? Поставьте «+».

8. Включение в систему знаний и повторение.

Повторение знаний о натуральных числах.

– С какими числами вы работали на уроке? (С двузначными, …)

– Какие еще числа вы знаете? (Однозначные, круглые, …)

– Все числа, с которыми вы работали на всех уроках в первом и во втором классе, называются … (натуральными).

Если дети не дают название, учитель говорит его сам.

Повесить карточку «натуральные числа».

– Их назвали так, потому что они служат для счёта предметов. Вспомните, что вы знаете о натуральных числах. Для этого я попрошу мне помочь… (назвать имена трёх учащихся).

– Сколько ребят стоит у доски? (3.)

– Что может обозначать число, если спросить «сколько»? (Количество предметов.)

Продолжить составление опорного сигнала:

– Что ещё может обозначать число 3.

Учитель измеряет шагами расстояние от одного из учеников, например, до стола. (Должно получиться 3 шага.)

– Что я измеряла? (Расстояние, длину.)

– Какую мерку я выбрала для измерения длины? (Шаг.)

– Сколько мерок уложилось при измерении величины? (3 мерки.)

– Что же в данном случае обозначает число 3? (Количество мерок при измерении длины.)

– А как измеряется любая величина? (Нужно выбрать мерку и посмотреть, сколько раз мерка уложится в измеряемой величине.)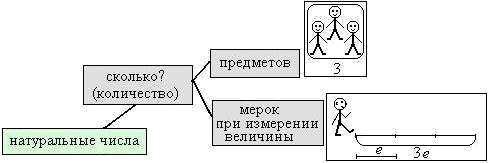

Продолжить составление опорного сигнала:

– Итак, вы выяснили, что число 3, да и любое другое натуральное число может обозначать…(количество предметов, количество мерок при измерении величины).

– Но это ещё не всё. Которым по счёту стоит?..

Назвать имя третьего по счёту ученика. Открыть часть карточки со словами «который по счёту».

(Третьим.)

– Что в данном случае обозначает число 3? (Порядок.)

Открыть вторую часть карточки – слово «порядок» и иллюстрацию. Опорный сигнал открыт полностью.

– Какие же числа называют натуральными? (Числа, которые служат для счёта предметов.)

– Что они еще могут обозначать? (Количество предметов, количество мерок при измерении величины, порядок при счёте.)

Открыть на доске: 1, 2, 3, 4…

– Посмотрите на ряд чисел? Как называется этот ряд? (Натуральный ряд чисел.)

– Какое следующее число? (5.)

– Назовите число, которое следует в натуральном ряду за числом 36, 57, 79. (37, 58, 80.)

– У каждого ли натурального числа есть последующее? (Да.)

– Как его получить? (Увеличить число на 1.)

– Назовите предыдущее чисел 28, 40, 91. (27, 39, 90.)

– У каждого ли натурального числа есть предыдущее? (Нет у числа 1.)

– Почему 0 не считают натуральным числом? (0 обозначает, что предметов нет, раз их нет, нельзя сосчитать их количество.)

– Существует ли самое большое натуральное число? (Нет.) А самое маленькое? (Число 1.)

– Существует ли самое маленькое двузначное число? (10) А самое большое? (99.)

– Итак, вы повторили всё, что знаете о натуральных числах и натуральном ряде чисел.

9. Рефлексия учебной деятельности на уроке.

– Что изменилось в ваших знаниях после сегодняшнего урока? (Мы узнали быстрый способ устных вычислений – по частям, повторили всё о натуральных числах…)

– Расскажите, как сложить или вычесть по частям. (…)

– Над чем каждому ещё надо поработать? (…)

– Оцените свою работу на уроке. Вы на уроке учились? Докажите. (…)

Домашнее задание.