УРОК-ЛЕКЦИЯ «КОМПЛЕКСНЫЕ ЧИСЛА И ОПЕРАЦИИ НАД НИМИ»

Шангина Ирина Евгеньевна, ГБОУ СОШ № 11 имени Героя Советского Союза Аипова М.И., учитель математики, Самарская область, г. Октябрьск

Предмет (направленность): математика.

Возраст детей: 10 класс.

Место проведения: класс.

Цель урока: познакомить учащихся с понятием комплексного числа; рассмотреть основные действия над комплексными числами.

Образовательные задачи:

1. Ввести понятие комплексного числа.

2. Показать алгебраическую и тригонометрическую формы комплексного числа.

3. Рассмотреть геометрическую интерпретацию комплексных чисел.

4. Познакомить с действиями над комплексными числами в алгебраической и тригонометрической формах.

Развивающие задачи:

1. Развивать мышление в процессе выполнения практических заданий.

2. Развивать пространственные представления.

Воспитывающие задачи:

1. Воспитывать культуру записей в тетради.

2. Воспитывать аккуратность, усидчивость, внимательность в процессе прослушивания лекции.

Тип урока: обзорная лекция.

План урока.

1. Организационный момент.

2. Изложение материала.

3. Домашнее задание.

4. Подведение итогов урока.

Ход урока

I. Организационный момент.

II. Изложение материала.

1. Мотивация.

Расширение множества вещественных чисел состоит в том, что к действительным числам присоединяются новые числа (мнимые). Введение этих чисел связано с невозможностью во множестве действительных чисел извлечения корня из отрицательного числа.

2. Введение понятия комплексного числа.

Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i² = - 1.

Исходя из этого, получим следующее определение комплексного числа.

Определение. Комплексным числом называется выражение вида a + bi, где a и b - действительные числа. При этом выполняются условия:

а) Два комплексных числа a₁ + b₁i и a₂ + b₂i равны тогда и только тогда, когда a₁=a₂, b₁=b₂.

б) Сложение комплексных чисел определяется правилом:

(a₁ + b₁i) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂) i.

в) Умножение комплексных чисел определяется правилом:

(a₁ + b₁i) (a₂ + b₂i) = (a₁a₂ - b₁b₂) + (a₁b₂ - a₂b₁) i.

3. Алгебраическая форма комплексного числа.

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

4. Действия над комплексными числами в алгебраической форме.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

1) Сложение.

Определение. Суммой комплексных чисел z₁ = a₁ + b₁i и z₂ = a₂ + b₂i называется комплексное число z, действительная часть которого равна сумме действительных частей z₁ и z₂, а мнимая часть - сумме мнимых частей чисел z₁ и z₂, то есть z = (a₁ + a₂) + (b₁ + b₂)i.

Числа z₁ и z₂ называются слагаемыми.

Сложение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁ + z₂ = z₂ + z₁.

2º. Ассоциативность: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃).

3º. Комплексное число –a –bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0

Пример 1. Выполните сложение (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Вычитание.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z, что z + z₂ = z₁.

Теорема. Разность комплексных чисел существует и притом единственна.

Пример 2. Выполните вычитание (4 – 2i) - (-3 + 2i).

(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.

3) Умножение.

Определение. Произведением комплексных чисел z₁=a₁+b₁i и z₂=a₂+b₂i называется комплексное число z, определяемое равенством: z = (a₁a₂ – b₁b₂) + (a₁b₂ + a₂b₁)i.

Числа z₁ и z₂ называются сомножителями.

Умножение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁z₂ = z₂z₁.

2º. Ассоциативность: (z₁z₂)z₃ = z₁(z₂z₃)

3º. Дистрибутивность умножения относительно сложения:

(z₁ + z₂) z₃ = z₁z₃ + z₂z₃.

4º. z · = (a + bi)(a – bi) = a² + b² - действительное число.

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

Пример 3. Выполните умножение (2 + 3i) (5 – 7i).

1 способ. (2 + 3i) (5 – 7i) = (2 5 – 3 (- 7)) + (2 (- 7) + 3 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.

2 способ. (2 + 3i) (5 – 7i) = 2 5 + 2 (- 7i) + 3i 5 + 3i (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.

4) Деление.

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

Пусть z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, тогда

.

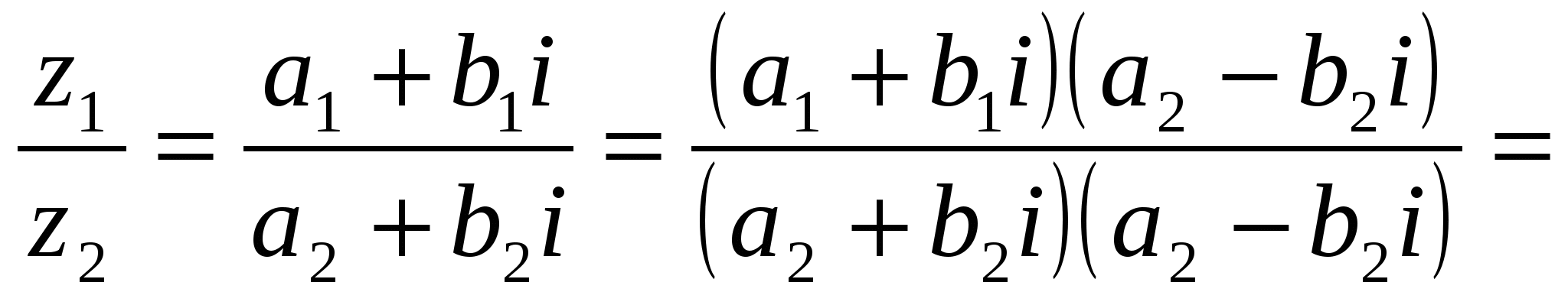
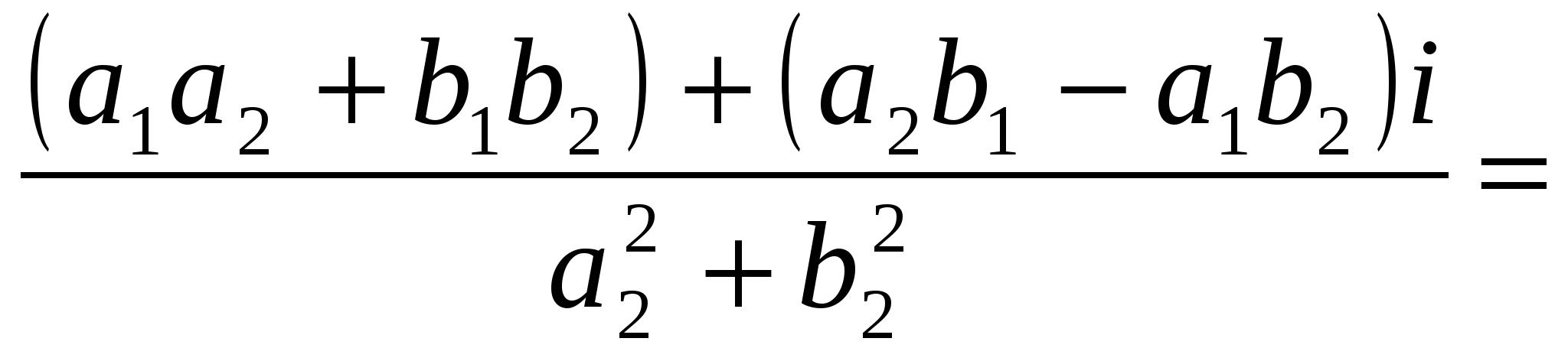
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Пример 4. Найти частное .

1 способ.

.

2 способ.

.

5) Возведение в целую положительную степень.

а) Степени мнимой единицы.

Пользуясь равенством i² = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:

i³ = i² i = -i,

i⁴ = i² i² = 1,

i⁵ = i⁴ i = i,

i⁶ = i⁴ i² = -1,

i⁷ = i⁵ i² = -i,

i⁸ = i⁶ i² = 1 и т. д.

Это показывает, что значения степени iⁿ, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 .

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

Пример 5. Вычислите: (i ³⁶ + i ¹⁷) · i ²³.

i ³⁶ = (i ⁴)⁹ = 1⁹ = 1,

i ¹⁷ = i ^{4 4+1} = (i ⁴)⁴ i = 1 · i = i.

i ²³ = i ^{4 5+3} = (i ⁴)⁵ i³ = 1 · i³ = - i.

(i ³⁶ + i ¹⁷) · i ²³ = (1 + i) (- i) = - i + 1= 1 – i.

б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.

Пример 6. Вычислите: (4 + 2i)³

(4 + 2i)³ = 4³ + 3 4² 2i + 3 4 (2i)² + (2i)³ = 64 + 96i – 48 – 8i = 16 + 88i.

5. Геометрическое изображение комплексных чисел.

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).

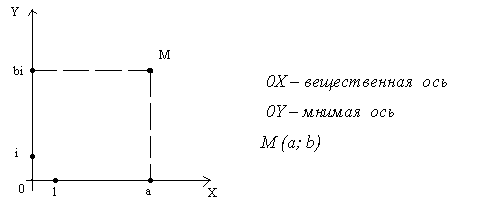
Рисунок 1

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).

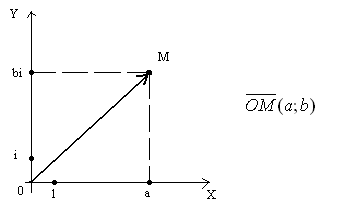
Рисунок 2

Пример 7. Постройте точки, изображающие комплексные числа: 1; - i; - 1 + i; 2 – 3i (рис.3).

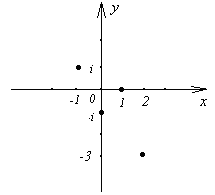
Рисунок 3

6. Тригонометрическая запись комплексных чисел.

Комплексное число z = a + bi можно задать с помощью радиус – вектора с координатами (a; b) (рис.4).

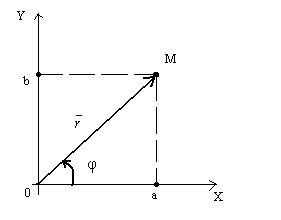
Рисунок 4

Определение. Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначается или r.

Для любого комплексного числа z его модуль r = | z | определяется однозначно по формуле .

Определение. Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументом этого комплексного числа и обозначается Аrg z или φ.

Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа z ≠ 0 – величина многозначная и определяется с точностью до слагаемого 2πк (к = 0; - 1; 1; - 2; 2; …): Arg z = arg z + 2πк, где arg z – главное значение аргумента, заключенное в промежутке (-π; π], то есть -π arg z ≤ π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0; 2π)).

a = r · cos φ, b = r · sin φ.

Следовательно, комплексное число z = a + bi можно записать в виде: z = r · cos φ + i r · sin φ или z = r · (cos φ + i sin φ).

Такая запись комплексного числа называется тригонометрической формой комплексного числа.

Пример 8. Представить в тригонометрической форме комплексное число 1– i.

a = 1, b = -1.

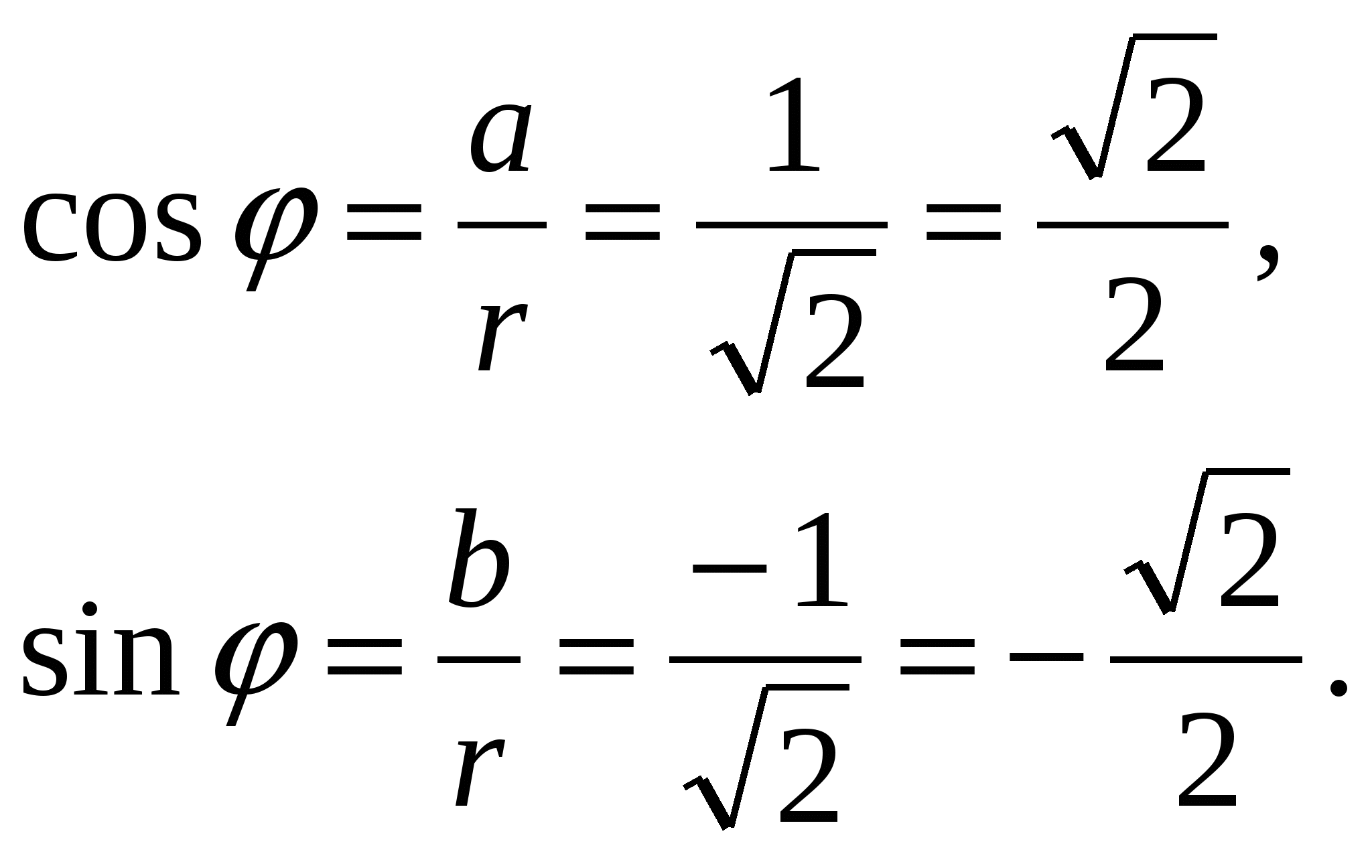
φ = .

1 – i = (cos + i sin ).

7. Действия над комплексными числами в тригонометрической форме.

1) Умножение.

Пусть два числа заданы и в алгебраической и в тригонометрической формах: z₁ = a₁ + b₁i = r₁ (cos φ₁ + i sin φ₁),

z₂ = a₂ + b₂i = r₂ (cos φ₂ + i sin φ₂).

На основании исходного определения правила умножения и формулы косинуса и синуса суммы получаем:

z_1· z₂ = r_{1 ·} r₂ (cos (φ₁ + φ₂) + i sin (φ₁ + φ₂)); r_{1 ·} r₂>0.

Умножение комплексных чисел в тригонометрической форме обладает следующими свойствами:

1º. Коммутативность: z₁z₂ = z₂z₁

2º. Ассоциативность: (z₁z₂) z₃ = z₁ (z₂ z₃).

Пример 9. Найти произведение комплексных чисел

z₁ = 2cos 50º + 2 i sin 50º, z₂ = cos 40º + i sin 40º.

Решение. Тригонометрические формы этих чисел имеют вид:

z₁ = 2 · (cos 50º + i sin 50º), z₂ = 1· (cos 40º + i sin 40º). Тогда

z₁ · z₂ = 1· 2 · (cos (50º + 40º) + i sin (50º + 40º)) = 2(cos 90º + i sin 90º) = = 2(0 + i) = 2i.

2) Деление комплексных чисел в тригонометрической форме.

Деление в поле комплексных чисел на числа, отличные от нуля, всегда выполнимо. Если числа z₁ и z₂ заданы в тригонометрической форме z₁ = r₁ (cos φ₁ + i sin φ₁), z₂ = r₂ (cos φ₂ + i sin φ₂), причем z₁ ≠ 0, то комплексное число является частным чисел z₁ и z₂(то есть z₁y = z₂).

Пример 10. Найти частное комплексных чисел z₁ = 2cos50º + 2i sin50º, z₂ = cos40º + i sin40º.

Решение. Тригонометрические формы этих чисел имеют вид:

z₁ = 2 · (cos50º + i sin50º), z₂ = 1· (cos40º + i sin40º).

Тогда (cos (50º - 40º) + i sin (50º - 40º)) = 2(cos10º + i sin10º).

3) Возведение в степень.

Определение. n – ой степенью комплексного числа z называется комплексное число, получающееся в результате умножения числа z самого на себя n раз.

Число z называется основанием степени, а натуральное число n – показателем степени.

Возвести комплексное число в n – ую степень можно по формуле:

z ⁿ = (r ⁿ) [cos (nφ) + i sin (nφ)].

Эту формулу при r =1 часто называют формулой Муавра:

(cos φ + i sin φ) ⁿ = cos (nφ) + i sin (nφ), n  N.

Пример 11. Вычислите (1 + i)¹⁰⁰.

Запишем комплексное число 1 + i в тригонометрической форме.

a = 1, b = 1.

.

cos φ = , sin φ = , φ = .

(1+i)¹⁰⁰ = [(cos + i sin)]¹⁰⁰= ()¹⁰⁰ (cos·100 + i sin·100) = = 2⁵⁰(cos 25π + i sin 25π) = 2⁵⁰(cos π + i sin π) = - 2⁵⁰.

4) Извлечение квадратного корня из комплексного числа.

При извлечении квадратного корня из комплексного числа a + bi имеем два случая:

если b > о, то ;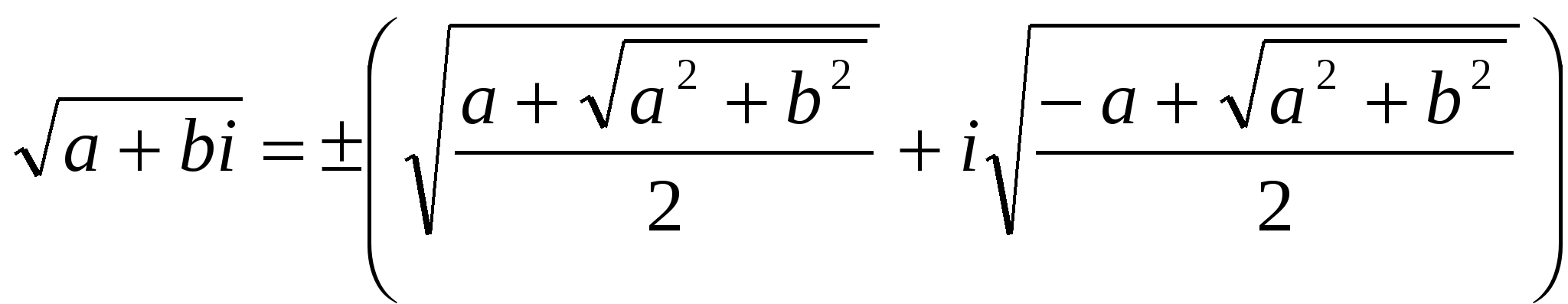

если b , то .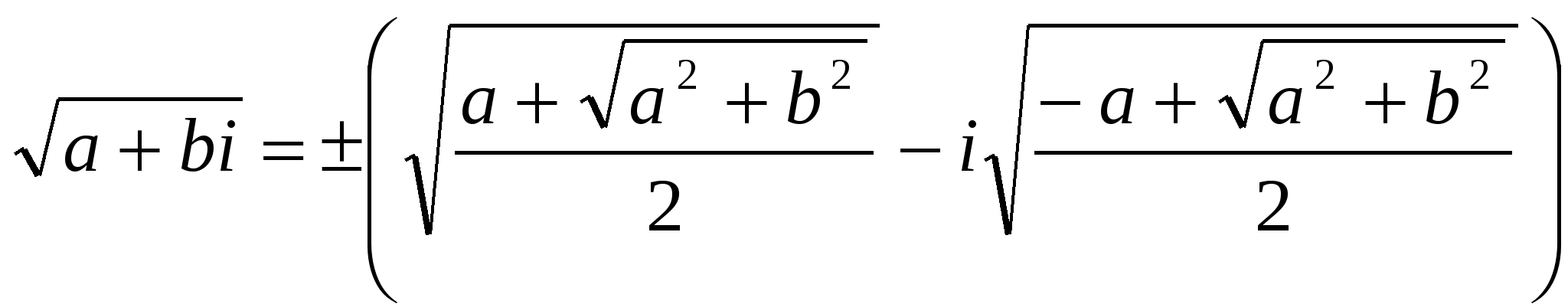

Так как из комплексного числа всегда можно извлечь квадратный корень, то любое квадратное уравнение всегда будет иметь решения во множестве комплексных чисел. Решения квадратного уравнения ах² + bх + с = 0 можно найти по известной формуле:

.

Пример 12. Вычислите .

Так как b , то воспользуемся формулой

.

= ,

= .

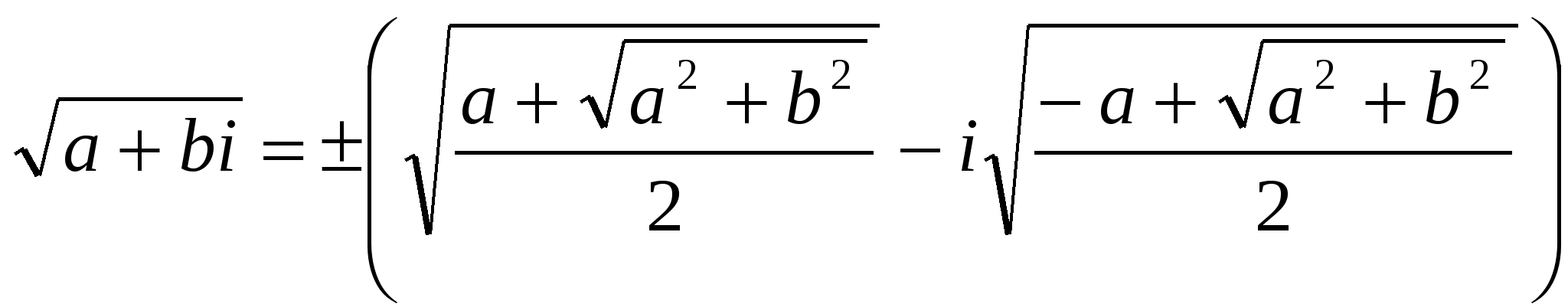
III. Домашнее задание.

Дома учащимся предлагается выполнить задание на повторение и закрепление пройденного материала.

1. Выполните действия.

а) ;

б) ;

в) .

2. Решите уравнения.

а) x² – 4x + 5 = 0;

б) y³ – 6y + 9 = 0.

IV. Подведение итогов урока.

ЛИТЕРАТУРА И ССЫЛКИ

1. Гусак А. А. Высшая математика. В 2-х т. Т. 1.: Учебник для студентов вузов. – 3-е изд., стереотип. Мн.: Тетра Системс, 2001. 544 с.

2. Кочетков Е. С., Кочеткова Е. С. Алгебра и элементарные функции. Учебное пособие для учащихся 10 класса средней школы. М.: Просвещение, 1975.

3. Кутепов А. К., Рубанов А. Т. Задачник по алгебре и элементарным функциям. М.: Высшая школа, 1974. 384 с.

4. Фаддеев Д. К., Соминский И. С. Алгебра. Ч. 2. Пособие для учителей средней школы.