ОРГАНИЗАЦИЯ ПОИСКА СПОСОБОВ РЕШЕНИЯ УРАВНЕНИЙ

Осипова Галина Владимировна, гимназия №86, учитель математики, Свердловская область

Предмет (направленность): уроки математики.

Возраст детей: 10-11 классы.

Место проведения: класс.

Аннотация

Учащиеся старших классов, владеющие способами решения уравнений разных видов, испытывают затруднения в поиске способов решения, т.к. по программе математики разные виды уравнений (а значит, и способы их решения) существуют отдельно, и учащиеся с трудом видят связь между ними, не могут увидеть известный способ решения в новом задании. Проблема в том, что старшеклассники не могут заменить один объект другим.

Организация такой деятельности возможна через групповую работу по поиску идеи, по индивидуальной работе с литературой, и, конечно, по решению уравнений. Особенно актуален этот вопрос в свете работы по новым ФГОС. Рассмотрим возможности такой работы на основе применения формул сокращенного умножения при решении уравнений.

Цель работы:

Обобщить известные учащимся способы решения уравнений

Задачи:

1. Выявить закономерности в формулах сокращенного умножения

2. Сформулировать выделенную закономерность (идею)

3. Придумать задачи с использованием выделенных закономерностей

4. Найти задачи с использованием этих идей

5. Показать практическое применение идей на решении конкретных заданий

Формулу разности квадратов знают, конечно, все старшеклассники, но вот замечают ее при решении уравнений только тогда, когда она дана в явном для использования виде.

Полезно поиграть с формулой:

При каких значениях переменных выражение (a + b)(a – b) равно 1? (например a=5, b=4)

Является точным квадратом? (например a=5, b=3)

Дает простое число?

Является иррациональным числом? И т.п.

После этого анализируем возможные ситуации.

Что дает нам равенство (a + b)(a – b) =1?

Можно одну скобку выразить через другую, то есть одно выражение заменить на сопряженное с ним (идея).

(a + b)(a – b) =1 a + b=1/(a – b) или a - b=1/(a + b)

Где это можно использовать?

Например, при решении уравнений. Заменой можно прийти к одной переменной.

А если произведение сопряженных выражений возвести в степень?

равенство не нарушилось! (идея)

А если рассмотреть не произведение, а сумму сопряженных выражений?

Например

Возведем полученное выражение в квадрат:

=

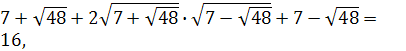
т.е. при возведении суммы (разности) сопряженных иррациональных выражений в квадрат, знаки корня пропадают (идея).

Теперь найденные идеи надо реализовать, и учащиеся начинают менять объекты в уравнениях, составляя такие, которые подчинены их идее, для которых их идея становится ключом к решению составленной задачи.

После того, как учащиеся наигрались с объектами, им предлагается выбрать из любых сборников задач уравнения, в которых заложены найденные ими идеи. Для классов естественно-математического профиля знаком «Сборник задач по математике для поступающих во ВТУЗы» под редакцией М.И.Сканави (1994г), и они подыскивают там задания согласно своих идей и, конечно, решают.

Применение идей:

№7.182(идея 2)

Решить уравнение

Решение. Т.к. , то

Получим

Пусть , a>0, тогда уравнение примет вид

или

Обратная замена

или

х = 2 или х = -2

Ответ. х=±2

№7.350(идея 2)

Решить уравнение

Решение. Т.к. , то

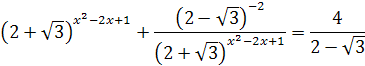
Пусть , у>0, тогда уравнение примет вид

или

Замена

Обратная замена

или

у=1 или

Обратная замена

или

или х=1 или

Ответ. х=1 или

№7.028 (идея 1)

Решение.

Т.к. , то

Получим или

Пусть , а>0

Откуда а=1 и а= -100, что не удовлетворяет условию а>0

а=1 , , х= ±1

Ответ. х= ±1

Вновь вернемся к формуле

Заменим объекты

Получили иррациональное уравнение, которое содержит корни только в одной части (идея).

Применение идеи:

№5.480 (идея 4)Решение. Применяем идею, домножая на сопряженное выражение левую и правую часть уравнения:

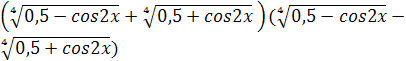= Получили:

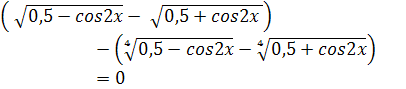
= или

)

или

Второе уравнение корней не имеет.

Ответ.

Согласно этих идей учащиеся находят много заданий из «Сборник задач по математике для поступающих во ВТУЗы» под редакцией М.И.Сканави, но, как правило, выбирают решать «интересные», т.е. те, в которых нестандартное видение ситуации:

№2.038

№2.277

№ 2.289

-

Исследуем выражения

и т.д.

т.е. сумму степеней сопряженных выражений можно преобразовать в другой вид (идея).

Как использовать? Заметим, что

, т.е. уравнение можно записать в виде

и решить как биквадратное (идея).

А уравнение к приводится к виду

и тоже решается заменой (идея).

Применение идеи:

№2.257(идея 5)

Решение. Замечаем четвертые степени, значит, можно свести к квадратному. Преобразуем:

Замена: t=x+4 Имеем

Применяем идею:

, m≥0, , m= -3,5 m=0,5.

m= -3,5 не удовлетворяет условию m≥0

m=0,5 0,5 t=

t=x+4 , значит x+4 = х=

Ответ. х=

№2.259(идея 5)

Решение. Преобразуем:

Замена: a =x-3 Имеем

Применяем идею:,

,

, n≥0,

По теореме Безу n=1 корень уравнения,

n= = не удовлетворяет условию n ≥0

n=1 a=±1 x-3=±1 х= -2, х= 4

Ответ. х= -2, х= 4

Игра с математическими объектами позволяет особенную организацию занятия, когда учащемуся не навязывается решение того или иного задания, а когда он сам начинает разгадывать идеи составления задач, сам конструировать задачи.

В процессе работы учащиеся перестают испытывать чувство разочарования, когда не могут решить задачу, а восторг разгаданной тайны позволяет процесс учения превратить в радость познания нового.