Конспект урока «Сорок мгновений наедине с корнем степени n» по математике для 10 класса
Здравствуйте ребята!
Тема сегодняшнего урока: «Сорок мгновений наедине с корнем степени n».
Цели:
-
Закрепить свойства степени n в ходе выполнения упражнений;
-
Познакомиться с оригинальными приемами решения примеров, содержащих корни степени n;
-
Наш урок призван не только закреплять навыки решения этих примеров, но и главное – развивать ваше мышление.
А начать наш урок я хочу с высказываний известных математиков, которые внесли большой вклад в развитие свойств корней степени n.
(слайды)
- Они говорят…
Что они говорят…
Пусть они говорят…
Истинное мнение ведет нас к правильным действиям.
С. Стевин
Мысль стремиться стать действием.
И. Ньютон
И я надеюсь, эти высказывания будут девизом работы на уроке.
1.Начнем урок с проверки домашней работы.
Консультанты докладывают о выполнении домашней работы.
1 ученик работает по компьютеру, 5 получают карточки.
Карточка №1
-
Вычислите:
![]()
-
Вынесите множитель за знак корня:(а>0; b>0)
![]()
-
Внесите множитель под знак корня: (а>0; b>0)
![]()
Карточка №2
-
Найдите значение числового выражения:
![]() .
.
-
Вынесите множитель за знак корня: (а>0; b>0)
![]()
-
Внесите множитель под знак корня: (а>0; b>0)
![]()
Карточка №3
Вычислите:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Карточка №4
Упростите выражение:
![]() ;
; ![]() .
.
Карточка №5
Вычислите:
![]()
Внесите под знак корня множитель:
![]()
![]()
Пока ребята работают самостоятельно, мы с вами поработаем устно:
-
Имеют ли смысл выражения:
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
-
Найти область определения выражений:
а ) ![]() ; б)
; б) ![]() ;в)
;в) ![]() .
.
Вывод: (самостоятельно)
-
Корень нечетной степени существует из любого числа;
-
Корень четной степени определен только для неотрицательных чисел.
-
Расположите в порядке убывания:
![]() ,
, ![]() ,
, ![]() .
.
-
Избавьтесь от иррациональности в знаменателе:
![]() ,
, ![]()
![]()
2.Решаем на доске все вместе
Я обЪясняю №3.79(д)
№3.79 9 (а,бв,г)
3. На дом я дала примеры, решение которых требует оригинальных приемов.Я обращаю ваше внимание на актуальность этих упражнений. Потому что на ЕГЭ, который вам предстоит сдавать в следующем году, решение этих заданий оценивается большим количеством баллов.
1 ученица на компьютере презентация
Доказать, что:
![]()
![]()
Решение:
пусть![]()
![]() ,тогда по условию m+n=4
,тогда по условию m+n=4
Найдем произведение m![]() n=
n=![]()
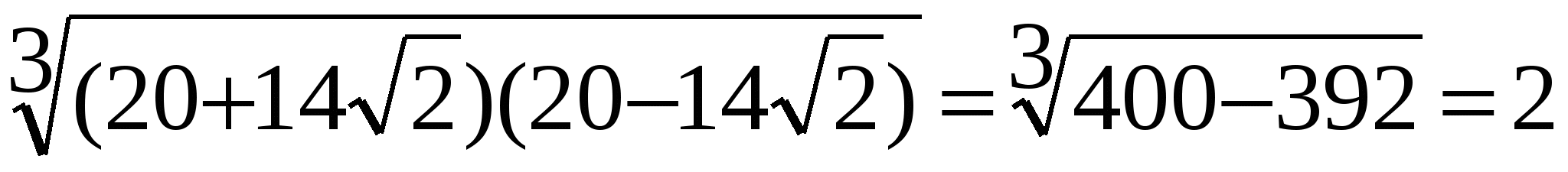 ,т.е. m
,т.е. m![]() n=2
n=2
Получаем: 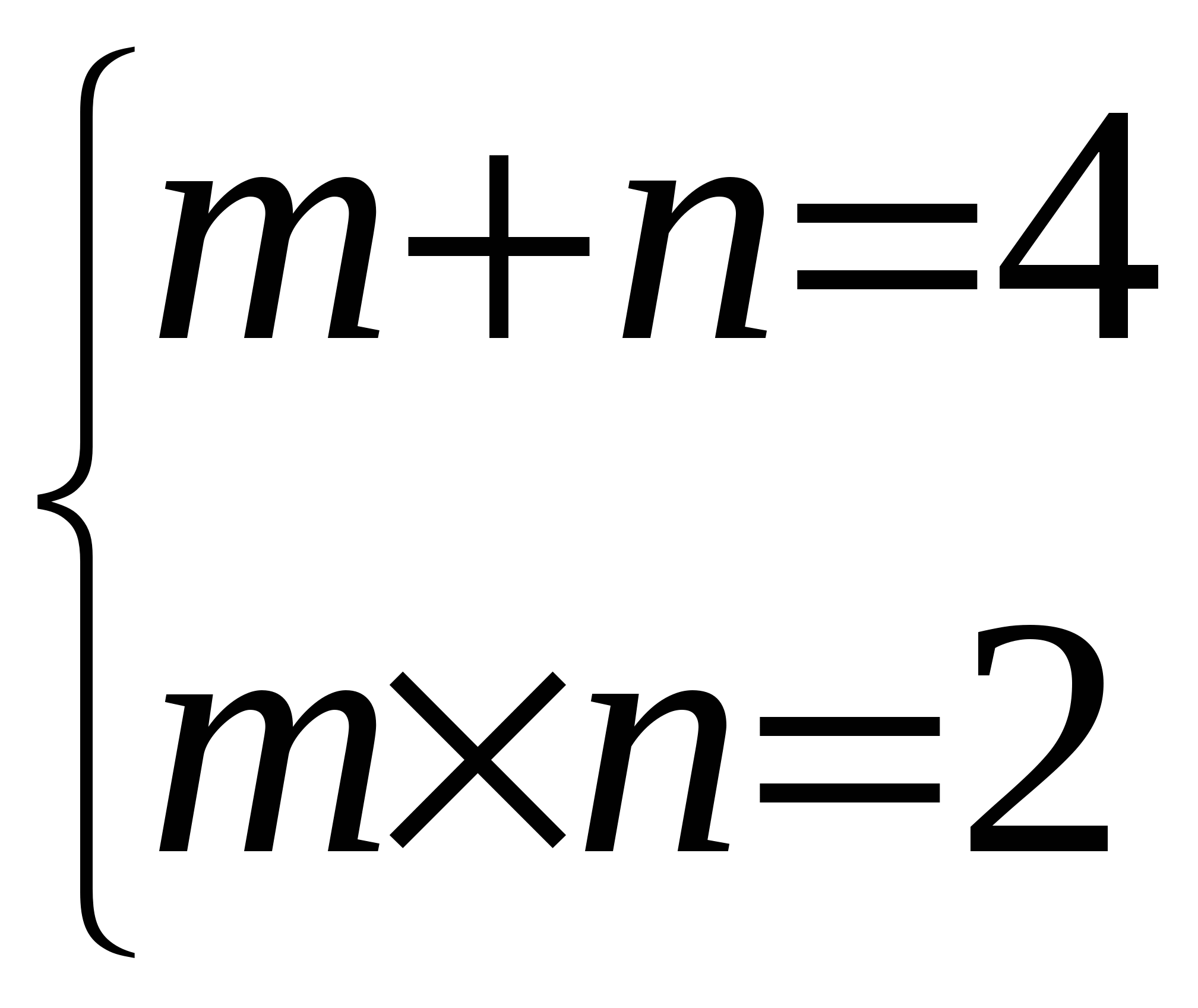 , следовательно m и n являются корнями квадратного уравнения:
, следовательно m и n являются корнями квадратного уравнения:
![]()
D1=4-2=2
![]()
![]()
т.е.
![]()
![]()
![]()
Что и требовалось доказать.
Домашнее задание:
Проверь равенство:
![]()
2 ученица объясняет решение задачи индийского математика Бхаскары.
Доказать:
![]()
Доказательство:
Возведём обе части уравнения в квадрат, учитывая что обе части равенства положительны и
![]()
Получим:
![]()
![]()
![]()
Что и требовалось доказать.
Итак, мы рассмотрели 2 нестандартных приема: введение новых переменных и возведение обеих частей равенства в квадрат.
4.А сейчас мы решим задание, которое часто предлагается на олимпиадах, а теперь уже и на ЕГЭ.
Представьте выражение в виде дроби, знаменатель которой не содержит радикала:
![]()
-
Самостоятельная работа.
ТЕСТЫ.
![]()
а ) 5; б) 0,5; в) -0,5; г) -5.
2. ![]()
а ) -![]() ; б) -1
; б) -1![]() ; в)
; в) ![]() ; г) не существует.
; г) не существует.
3. Вычислить:
![]()
![]()
а ) 9; б) 18; в) 6; г) 24
4. Какие из данных выражений имеют смысл:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() :
:
а ) нет таких; б) 2;3. В) 3; г) 2.
5.Упростить:
![]()
а ) а+2; б) –а-2; в) ![]() ; г) а-2.
; г) а-2.
Вариант 2
![]()
а ) -0,3; б) 3; в) 0,3; г) ![]() .
.
2. ![]()
а ) -1![]() ; б)
; б) ![]() ; в) 1
; в) 1![]() ; г) не существует.
; г) не существует.
3. Вычислить:
![]()
![]()
а ) 9; б) 18; в) 6; г) 24
4. Какие из данных выражений имеют смысл:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() :
:
а ) нет таких; б) 2;3. В) 3; г) 2.
5.Упростить:
![]()
а ) а+2; б) –а-2; в) ![]() ; г) а-2.
; г) а-2.
Домашнее задание: №3.79(е), 3.80.
-
Итак, наш урок подошел к концу. Что нового узнали.
А закончить наш урок хочется притчей. Встретил однажды старец трех работников, строивших церковь. Они шли уставшие. Старец спросил их: «Почему они такие уставшие?» Первый ответил: « Я много работал, строил здание».
Второй: «Я устал, потому что строил церковь».
А третий, спокойно ответил: «Я строил храм».
И сегодня мне хотелось бы, чтобы ответом на вопрос: «Чем вы занимались на уроке», были слова третьего работника: «Мы прокладывали дорогу к храму науки, имя которому Математика».
Итак, 40 мгновений наедине с корнем степени n пролетели.
До свидания!
Карточка №1
1.Вычислите:
![]()
2.Вынесите множитель за знак корня:(а>0; b>0)
![]()
3.Внесите множитель под знак корня: (а>0; b>0)
![]()
Карточка №2
1.Найдите значение числового выражения:
![]() .
.
-
Вынесите множитель за знак корня: (а>0; b>0)
![]()
-
Внесите множитель под знак корня: (а>0; b>0)
![]()
Карточка №3
Вычислите:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Карточка №4
Упростите выражение:
![]() ;
; ![]() .
.
Карточка №5
Вычислите:
![]()
Внесите под знак корня множитель:
![]()
![]()
Вариант 1
![]()
а ) 5; б) 0,5; в) -0,5; г) -5.
2. ![]()
а ) -![]() ; б) -1
; б) -1![]() ; в)
; в) ![]() ; г) не существует.
; г) не существует.
3. Вычислить:
![]()
![]()
а ) 9; б) 18; в) 6; г) 24
4. Какие из данных выражений имеют смысл:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() :
:
а ) нет таких; б) 2;3. В) 3; г) 2
5.Упростить:
![]()
а ) а+2; б) –а-2; в) ![]() ; г) а-2.
; г) а-2.
Вариант 2
![]()
а ) -0,3; б) 3; в) 0,3; г) ![]() .
.
2. ![]()
а ) -1![]() ; б)
; б) ![]() ; в) 1
; в) 1![]() ; г) не существует.
; г) не существует.
3. Вычислить:
![]()
а ) 9; б) 18; в) 2; г) 36
4. Какие из данных выражений имеют смысл:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
а )1;3 б) 2; В) 3 ; г) 1.
5.Упростить:
![]()
а )-х-2; б) х+2 в) х-2; г) ![]() .
.
Здесь представлен конспект к уроку на тему «Сорок мгновений наедине с корнем степени n», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

