Конспект урока «Площадь параллелограмма» по геометрии для 9 класса

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №2 с.Октябрьское»

МО – Пригородный район РСО - Алания

Разработка открытого урока

по математике

в 9 классе по теме:

«Площадь параллелограмма».

Выполнила:

Учитель математики

Плиева Л. Б.

Тема: «Площадь параллелограмма».

Цель:

1. - общеобразовательная: систематизировать знания, умения и навыки в применении основных формул для нахождения площади параллелограмма

2. - развивающая: развитие интеллектуальных способностей учащихся, расширение их кругозора, формирование умения логически мыслить;

3. - воспитательная: воспитывать трудолюбие, усердие, сообразительность, умение слушать других и высказывать свою точку зрения.

Девиз урока: «Занятия математикой – это такая гимнастика ума,

для которой нужны вся гибкость

и вся выносливость молодости»

ХОД УРОКА

I. Организационный момент.

проверка готовности класса к уроку: наличие учебников, тетрадей, чертёжных инструментов.

II.Проверка домашнего задания.

Один из учащихся заранее подготовил оформление решения домашнего задания. Упражнение 7. Задача полностью разбирается. Заострить внимание на правильности оформления задачи

Ш. Устные упражнения.

1.Найдите стороны параллелограмма, зная что его периметр 24.

а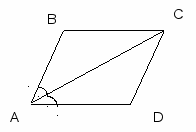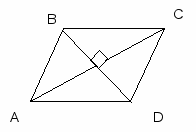) б)

2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.

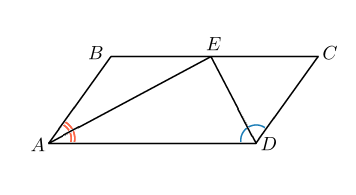
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.

Углы  и , а также  и  — накрест лежащие. Накрест лежащие углы равны. Значит, угол  равен углу , а угол  — углу . 
Получаем, что треугольники  и  — равнобедренные, то есть , а . Тогда 

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник

IY. Практическая работа.

А) Дан параллелограмм – получить прямоугольник.

Б)  Дан прямоугольник – получить параллелограмм.

Разрезать исходную фигуру на две части (произвести только одно разрезание), чтобы потом из разрезанных частей сконструировать заданную фигуру.

Подвести учащихся к тому, чтобы наглядно видели, что площади получившихся фигур равны.

Y. Проблемный вопрос: Как найти площадь параллелограмма?

Материал, рассмотренный на предыдущих этапах урока, позволяет привести учащихся к мысли, что надо параллелограмм “перекроить” в другую фигуру, площадь которой они умеют вычислять. Решение поставленной задачи проводится совместными исследованиями и обоснованиями учителя и учащихся, используя наглядные возможности.

Проведем в параллелограмме АВСD высоты ВН и СК. Что можно сказать об отрезках АВ и СD? Каковы отрезки ВН и СК? Почему?

Ответ: они равны как противолежащие стороны параллелограмма и как расстояния между параллельными прямыми.

-Тогда что вы можете сказать о треугольниках АВН и DСК? Почему?

Ответ: они прямоугольные и равны по гипотенузе и катету.

-А что мы знаем о площадях равных фигур?

-Их площади равны.

-Вернемся к параллелограмму и выясним из каких двух фигур он состоит.

Ответ: из треугольника АВН и трапеции НВСD.

-Переместим треугольник АВН, тем самым “перекроим” параллелограмм в фигуру НВСК, из каких многоугольников состоит она?

Ответ: из трапеции НВСD и треугольника DСК.

-Что можно сказать о фигурах АВСD и НВСК.

-Они равновелики по разложению, значит, их площади равны.

-Чем является фигура НВСК?

-Прямоугольником, так как это параллелограмм с прямыми углами.

-Чему равна площадь НВСК?

-Произведению длин НК и ВН – смежных сторон прямоугольника.

-Каким отрезком параллелограмма можно заменить отрезок НК?

-Отрезком АD. Так как НК = ВС = АD.

-Итак, чему же равна площадь АВСD?

-Произведению длин отрезков АD и ВН.

-Какой вывод мы можем сделать из проведенного исследования, как же найти площадь параллелограмма АВСD?

-Провести высоту ВН и найти произведение длин отрезков АD и ВН.

Сторону АD параллелограмма иногда называют основанием.

-А если в качестве основания взять сторону СD и провести к ней высоту ВК, то как мы найдем площадь параллелограмма?

-Площадь можно найти, умножив длину СD на длину ВК.

-Таким образом, как мы можем сформулировать правило нахождения площади параллелограмма?

-Площадь параллелограмма равна произведению длины его стороны на высоту, проведенную к этой стороне.

Сформулированное нами правило мы докажем с вами как теорему.

Дано: ABCD-параллелограмм

Доказать: S=AD*BH

Доказательство:

трапеция ABCK составлена из параллелограмма и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH. Прямоугольные треуг. DCK и ABH равны (по гипотенузе и острому углу), поэтому их площади равны =>

Площади ABCD и HBCK также равны, т.е. площадь прямоугольника HBCK равна S. По теореме =>

S=BC*BH, а так как BC=AD,то S=AD*BH

Запишем  еще одну формулу площади параллелограмма:

 , где  и  — стороны параллелограмма,  — угол между ними.

Так же, как и свойства биссектрис углов параллелограмма, эта формула пригодится тем, кто нацелен на решение задачи .

, где  и  — диагонали параллелограмма,  — угол между ними.

1

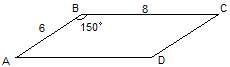
Стороны параллелограмма равны 10 см и 6 см, а угол между ними 150º. Найдите площадь этого параллелограмма.

2

Острый угол параллелограмма равен 30º, а высоты, проведенные из вершины тупого угла равны 4 см и 3 см. Найдите площадь этого параллелограмма.

YI. Итоги нашего урока.

1. Достигли мы поставленной цели?

Ответ: Да, мы узнали новую формулу для вычисления площади параллелограмма.

2. Какой главный итог нашего урока?

Ответ: Исследовали и доказали способ отыскания площади любого параллелограмма по известным значениям стороны и высоты, проведенной к этой стороне.

YII. Домашнее задание:

теорема о площади параллелограмма. Вывести формулу для вычисления площади параллелограмма . Упр.10,11.

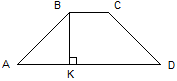
1. ABCD – параллелограмм, ВН=8 см. Найти: ВК.(4,8)

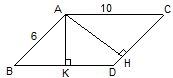
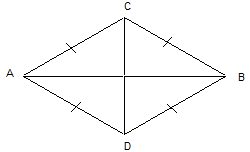
2. ABCD – параллелограмм. Найти: площадь ABCD.(24)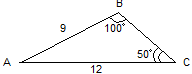

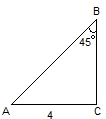
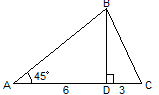
3. Найти: площадь АВС.(8)

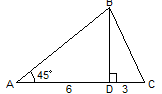
4. Найти: площадь АВС.(27)

5. Найти: площадь АВС.(27)

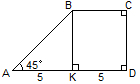
6. Найти: площадь АВС.(36)

7. АС=12, площадь ABCD равна 48. Найти: BD.(8)

8. ABCD – трапеция, ВС:AD=2:3; ВК=6, площадь ABCD равна 60. Найти: ВС, AD.(8, 12)

9. Найти: площадь АВСD.(37,5)

3. Самостоятельная работа.

I уровень

1 Вариант

1. Сторона параллелограмма равна 21 см, а высота, проведенная к ней 15 см. Найдите площадь параллелограмма.

2. Сторона треугольника равна 5 см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника.

3. В трапеции основания равны 6 и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.

4. Стороны параллелограмма равны 6 и 8 см, а угол между ними равен 30º. Найдите площадь параллелограмма.

5. Диагонали ромба относятся как 2:3, а их сумма равна 25 см. Найдите площадь ромба.

2 Вариант

1. Сторона параллелограмма равна 17 см, а его площадь 187 см². Найдите высоту, проведенную к данной стороне.

2. Сторона треугольника равна 18 см, а высота, проведенная к ней, в 3 раза меньше стороны. Найдите площадь треугольника.

3. В трапеции основания равны 4 и 12 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.

4. Стороны параллелограмма равны 4 и 7 см, а угол между ними равен 150º. Найдите площадь параллелограмма.

5. Диагонали ромба относятся как 3:5, а их сумма равна 8 см. Найдите площадь ромба.

II уровень

1 Вариант

1. В равнобедренном треугольнике АВС высота ВН равна 12 см, а основание АС а 3 раза больше высоты ВН. Найдите площадь треугольника АВС.

2. В параллелограмме ABCD стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4 см. Найдите площадь параллелограмма и вторую высоту.

3. Площадь трапеции равна 320 см², а высота трапеции равна 8 см. Найдите основания трапеции, если длина одного из оснований составляет 60% длины другого.

4. В треугольнике АВС стороны АВ и ВС равны соответственно 14 и 18 см. Сторона АВ продолжена за точку А на отрезок АМ, равный АВ. Сторона ВС продолжена за точку С на отрезок КС, равный половине ВС. Найдите площадь треугольника МВК, если площадь треугольника АВС равна 126 см².

5. В ромбе АВСК из вершин В и С опущены высоты ВМ и СН на прямую АК. Найдите площадь четырехугольника МВСН, если площадь ромба равна 67 см².

2 Вариант

1. В равнобедренном треугольнике АВС высота АН в 4 раза меньше основания ВС, равного 16 см. Найдите площадь треугольникаАВС.

2. В параллелограмме ABCD высоты равны 10 и 5 см, площадь параллелограмма равна 60 см². Найдите стороны параллелограмма.

3. В равнобокой трапеции АВСМ большее основание АМ равно 20 см, высота ВН отсекает от АМ отрезок АН, равный 6 см. УголВАМ равен 45º. Найдите площадь трапеции.

4. В ромбе ABCD на стороне ВС отмечена точка К такая, что КС:ВК=3:1. Найдите площадь треугольника АВК, если площадь ромба равна 48 см².

5. В треугольнике АВМ через вершину В проведена прямая d, параллельная стороне АМ. Из вершины А и М проведены перпендикуляры АС и MD на прямую d. Найдите площадь четырехугольника ACDM, если площадь треугольника АВМ равна 23 см².

4. Итог урока.

Продолжите фразу:

«Сегодня на уроке мы повторили …»

«Сегодня на уроке мы закрепили…»

«Сегодня на уроке мы узнали…»

Что было для вас на уроке интересного? Что не понравилось?

Оценки за урок.