Конспект урока «Колебательный контур. Свободные электромагнитные колебания. Превращение энергии в колебательном контуре. Формула Томпсона» по физике
Урок № 48-169 Колебательный контур. Свободные электромагнитные колебания. Превращение энергии в колебательном контуре. Формула Томпсона.
Колебания — движения или состояния, повторяющиеся во времени.
Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения.
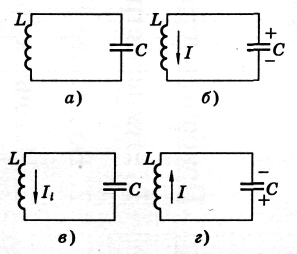 Колебательный контур — это система, состоящая из катушки индуктивности и конденсатора (рис. а).
Колебательный контур — это система, состоящая из катушки индуктивности и конденсатора (рис. а).
Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет течь в ту же сторону и перезарядит конденсатор (рис. в).
Ток в данном направлении прекратится, и процесс повторится в обратном направлении (рис. г).
Таким образом, в колебательном контуре происходят электромагнитные колебания из-за превращения энергии электрического поля конденсатора (WЭ= ![]() ) в энергию магнитного поля катушки с током (WМ =
) в энергию магнитного поля катушки с током (WМ =![]() ), и наоборот.
), и наоборот.
Гармонические колебания - периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса.
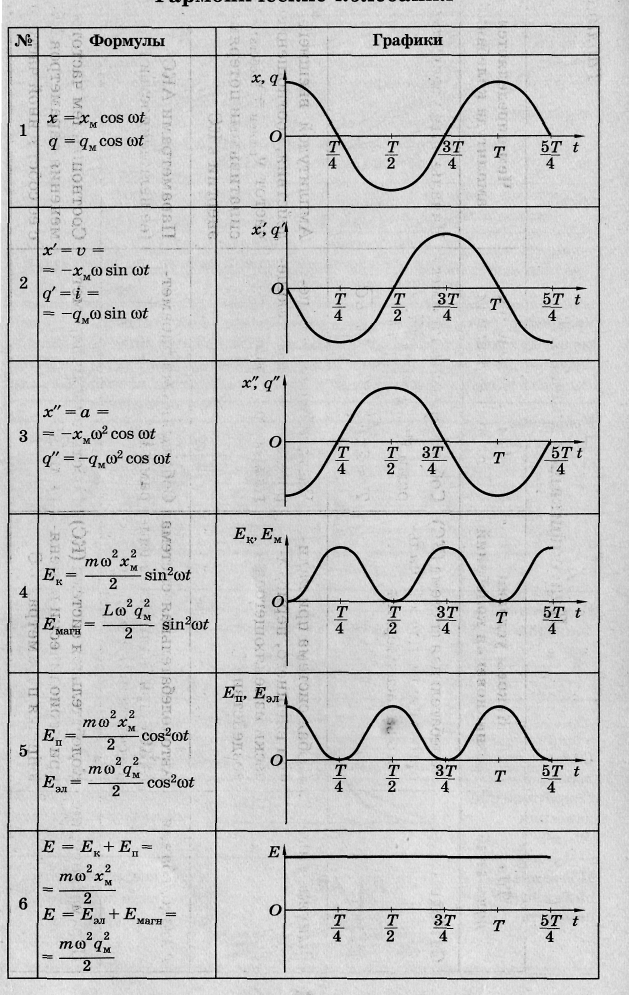 Уравнение, описывающее свободные электромагнитные колебания, принимает вид
Уравнение, описывающее свободные электромагнитные колебания, принимает вид
q"= — ω02q (q"- вторая производная.
Основные характеристики колебательного движения:
Период колебаний - минимальный промежуток времени Т, через который процесс полностью повторяется.
Амплитуда гармонических колебаний - модуль наибольшего значения колеблющейся величины.
Зная период, можно определить частоту колебаний, т. е. число колебаний в единицу времени, например в секунду. Если одно колебание совершается за время Т, то число колебаний за 1 с ν определяется так: ν = 1/Т.
Напомним, что в Международной системе единиц (СИ) частота колебаний равна единице, если за 1 с совершается одно колебание. Единица частоты называется герцем (сокращенно: Гц) в честь немецкого физика Генриха Ге р ц а.
Через промежуток времени, равный периоду Т, т. е. при увеличении аргумента косинуса на ω0Т, значение заряда повторяется и косинус принимает прежнее значение. Из курса математики известно, что наименьший период косинуса равен 2л. Следовательно, ω0Т =2π,откуда ω0= ![]() =2πν Таким образом, величина ω0 — это число колебаний, но не за 1 с, а за 2л с. Она называется циклической или круговой частотой.
=2πν Таким образом, величина ω0 — это число колебаний, но не за 1 с, а за 2л с. Она называется циклической или круговой частотой.
Частоту свободных колебаний называют собственной частотой колебательной системы. Часто в дальнейшем для краткости мы будем называть циклическую частоту просто частотой. Отличить циклическую частоту ω0 от частоты ν можно по обозначениям.
По аналогии с решением дифференциального уравнения для механической колебательной системы циклическая частота свободных электрических колебаний равна:ω0=![]()
Период свободных колебаний в контуре равен: Т=![]() =2π
=2π![]() - формула Томсона.
- формула Томсона.
Фаза колебаний (от греческого слова phasis – появление, ступень развития какого-либо явления) – величина φ, стоящая под знаком косинуса или синуса. Выражается фаза в угловых единицах – радианах. Фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.
Колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами.
Так как ω0= ![]() , то φ= ω0Т=2π
, то φ= ω0Т=2π![]() . Отношение
. Отношение ![]() показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. Так, по прошествии времени t=
показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. Так, по прошествии времени t=![]() (четверти периода) φ=
(четверти периода) φ=![]() , по прошествии половины периода φ = π, по прошествии целого периода φ=2π и т.д.Можно изобразить на графике зависимость
, по прошествии половины периода φ = π, по прошествии целого периода φ=2π и т.д.Можно изобразить на графике зависимость
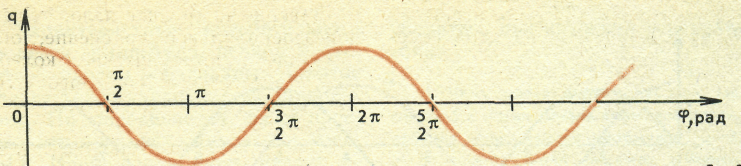 заряда не от времени, а от фазы. На рисунке показана та же косинусоида, что и на предыдущем, но на горизонтальной оси отложены вместо времени
заряда не от времени, а от фазы. На рисунке показана та же косинусоида, что и на предыдущем, но на горизонтальной оси отложены вместо времени
различные значения фазы φ.
Соответствие между механическими и электрическими величинами в колебательных процессах
| Электрические величины | |
| Координата x | Заряд q |
| Скорость v | Сила тока I |
| Масса т | Индуктивность L |
| Жесткость пружины k | Величина, обратная емкости |
| Потенциальная энергия | Энергия электрического поля |
| Кинетическая энергия | Энергия магнитного поля |
Задачи.
942(932). Начальный заряд, сообщенный конденсатору колебательного контура, уменьшили в 2 раза. Во сколько раз изменились: а) амплитуда напряжения; б) амплитуда силы тока;
в) суммарная энергия электрического поля конденсатора и магнитного поля катушки?
943(933). При увеличении напряжения на конденсаторе колебательного контура на 20 В амплитуда силы тока увеличилась в 2 раза. Найти начальное напряжение.
945(935). Колебательный контур состоит из конденсатора емкостью С = 400 пФ и катушки индуктивностью L = 10 мГн. Найти амплитуду колебаний силы тока Iт, если амплитуда колебаний напряжения Uт = 500 В.
952(942). Через какое время (в долях периода t/T) на конденсаторе колебательного контура впервые будет заряд, равный половине амплитудного значения?
957(947). Катушку какой индуктивности надо включить в колебательный контур, чтобы при емкости конденсатора 50 пФ получить частоту свободных колебаний 10 МГц?
Колебательный контур. Период свободных колебаний.
1. После того как конденсатору колебательного контура был сообщён заряд q = 10-5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нём полностью затухнут? Ёмкость конденсатора С=0,01мкФ.
2. Колебательный контур состоит из конденсатора ёмкостью 400нФ и катушки индуктивностью 9мкГн. Каков период собственных колебаний контура?
3. Какую индуктивность надо включить в колебательный контур, чтобы при ёмкости 100пФ получить период собственных колебаний 2∙ 10-6 с.
4. Сравнить жесткости пружин k1/k2 двух маятников с массами грузов соответственно 200г и 400г, если периоды их колебаний равны.
5. Под действием неподвижно висящего груза на пружине её удлинение было равно 6,4см. Затем груз оттянули и отпустили, вследствие чего он начал колебаться. Определить период этих колебаний.
6. К пружине подвесили груз, вывели его из положения равновесия и отпустили. Груз начал колебаться с периодом 0,5с. Определите удлинение пружины после прекращения колебаний. Массу пружины не учитывать.
7. За одно и то же время один математический маятник совершает 25 колебаний, а другой 15. Найти их длины, если один из них на 10см короче другого.
8. Колебательный контур состоит из конденсатора ёмкостью 10мФ и катушки индуктивности 100мГн. Найти амплитуду колебаний напряжения, если амплитуда колебаний силы тока 0,1А
9. Индуктивность катушки колебательного контура 0,5мГн. Требуется настроить этот контур на частоту 1МГц. Какова должна быть ёмкость конденсатора в этом контуре?
Экзаменационные вопросы:
1. Какое из приведенных ниже выражений определяет период свободных колебаний в колебательном контуре? А . ![]() ; Б.
; Б. ![]() ; В.
; В. ![]() ; Г.
; Г. ![]() ; Д. 2
; Д. 2![]() .
.
2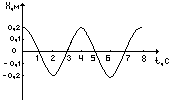 . Какое из приведенных ниже выражений определяет циклическую частоту свободных колебаний в колебательном контуре? А.
. Какое из приведенных ниже выражений определяет циклическую частоту свободных колебаний в колебательном контуре? А. ![]() Б.
Б. ![]() В.
В. ![]() Г.
Г. ![]() Д. 2π
Д. 2π![]()
3. На рисунке представлен график зависимости координаты Х тела, совершающего гармонические колебания вдоль оси ох, от времени. Чему равен период колебания тела?
А. 1 с; Б. 2 с; В. 3 с. Г. 4 с. Д. Среди ответов А-Г нет правильного.
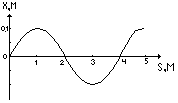
4. На рисунке изображён профиль волны в определённый момент времени. Чему равна её длина?
А. 0,1 м. Б. 0,2 м. В. 2 м. Г. 4 м. Д. 5 м.
5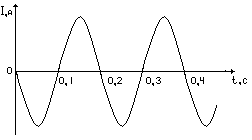 . На рисунке представлен график зависимости силы тока через катушку колебательного контура от времени. Чему равен период колебаний силы тока? А. 0,4 с. Б. 0,3 с. В. 0,2 с. Г. 0,1 с.
. На рисунке представлен график зависимости силы тока через катушку колебательного контура от времени. Чему равен период колебаний силы тока? А. 0,4 с. Б. 0,3 с. В. 0,2 с. Г. 0,1 с.
Д. Среди ответов А-Г нет правильного.
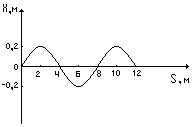
6. На рисунке изображён профиль волны в определённый момент времени. Чему равна её длина?
А. 0,2 м. Б. 0,4 м. В. 4 м. Г. 8 м. Д. 12 м.
7. Электрические колебания в колебательном контуре заданы уравнением q =10-2 ∙cos 20t (Кл).
Чему равна амплитуда колебаний заряда?
А. 10-2 Кл. Б.cos 20t Кл. В.20t Кл. Г.20 Кл. Д.Среди ответов А-Г нет правильного.
8. При гармонических колебаниях вдоль оси ОХ координата тела изменяется по закону X=0,2cos(5t+![]() ). Чему равна амплитуда колебаний тела?
). Чему равна амплитуда колебаний тела?
А. Xм; Б. 0,2 м; В. сos(5t+![]() ) м; (5t+
) м; (5t+![]() )м; Д.
)м; Д.![]() м
м
9. Частота колебаний источника волны 0,2 с-1 скорость распространения волны 10 м/с. Чему равна, длина волны? А. 0,02 м. Б. 2 м. В. 50 м.
Г. По условию задачи нельзя определить длину волны. Д. Среди ответов А-Г нет правильного.
10. Длина волны 40 м, скорость распространения 20 м/с. Чему равна частота колебаний источника волн?
А. 0,5 с-1. Б. 2 с-1. В. 800 с-1.
Г. По условию задачи нельзя определить частоту колебания источника волн.
Д. Среди ответов А-Г нет правильного.
http://megapost.info/promo/fra/
Здесь представлен конспект к уроку на тему «Колебательный контур. Свободные электромагнитные колебания. Превращение энергии в колебательном контуре. Формула Томпсона», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Физика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

