Конспект урока «Бенефис линейной функции» по математике для 7 класса
Тема урока: “Бенефис линейной функции” Слайд 1.
Цель урока: систематизировать знания учащихся по теме “Линейная функция, ее свойства и график”.
Оборудование: презентация, контрольные листы.
Ход урока
-
Оргмомент. Тема нашего урока “Бенефис линейной функции”. А что же такое бенефис? Я предлагаю вам обратиться к толковому словарю Даля. «БЕНЕФИС» - это спектакль, представление в пользу одного из участвующих. Кто же на нашем уроке будет актером, в пользу которого дается представление?
-
Повторение пройденного материала:
Устный фронтальный опрос.
-
Сформулируйте определение линейной функции.
-
(Линейной функцией называется функция, которую можно задать формулой вида
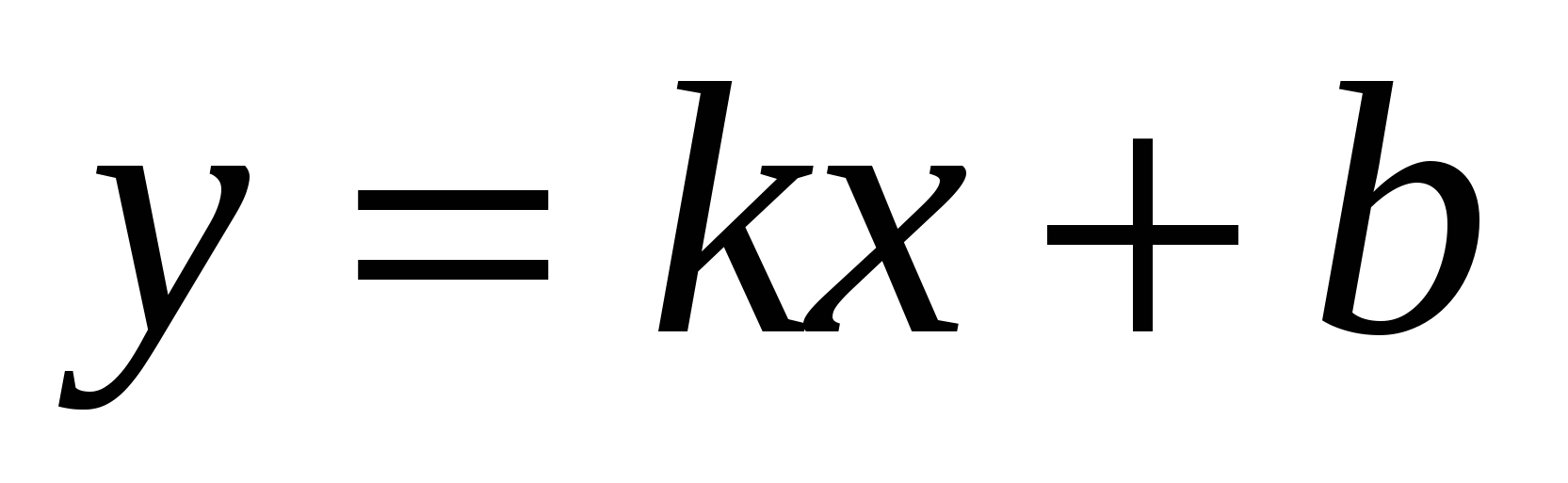 , где х – независимая переменная, k и b – некоторые числа.)
, где х – независимая переменная, k и b – некоторые числа.) -
Какие частные случаи линейной функции вам известны? (Первый случай, когда число b равно 0. Второй случай, когда число k равно 0)
-
Как называется функция у которой число b равно 0 и дайте ее определение. (Такая функция называется прямой пропорциональностью. Прямой пропорциональностью называется функция, которую можно задать формулой вида
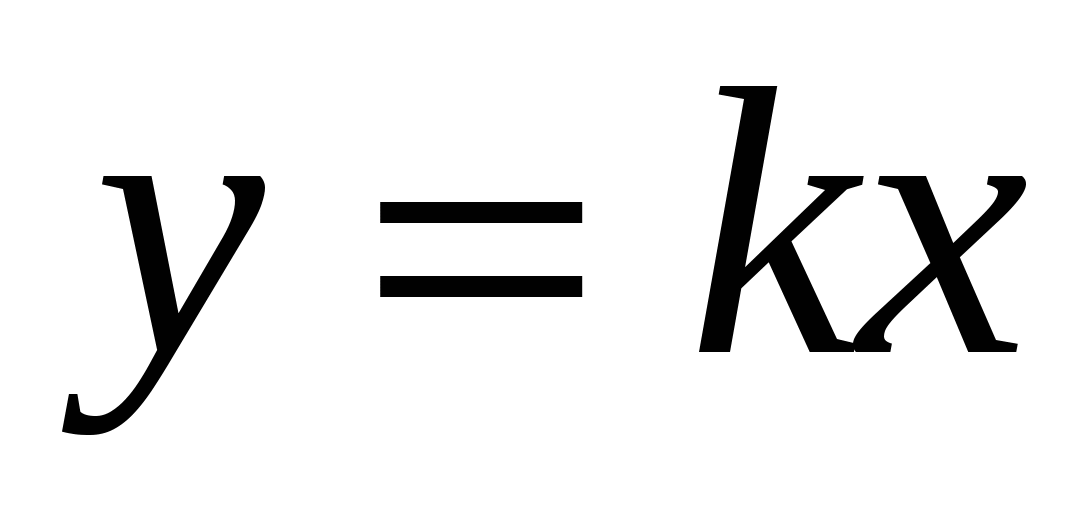 , где х – независимая переменная, k – не равное нулю число.)
, где х – независимая переменная, k – не равное нулю число.) -
Какой формулой задается функция у которой число k равно нулю? (Такая функция задается формулой вида
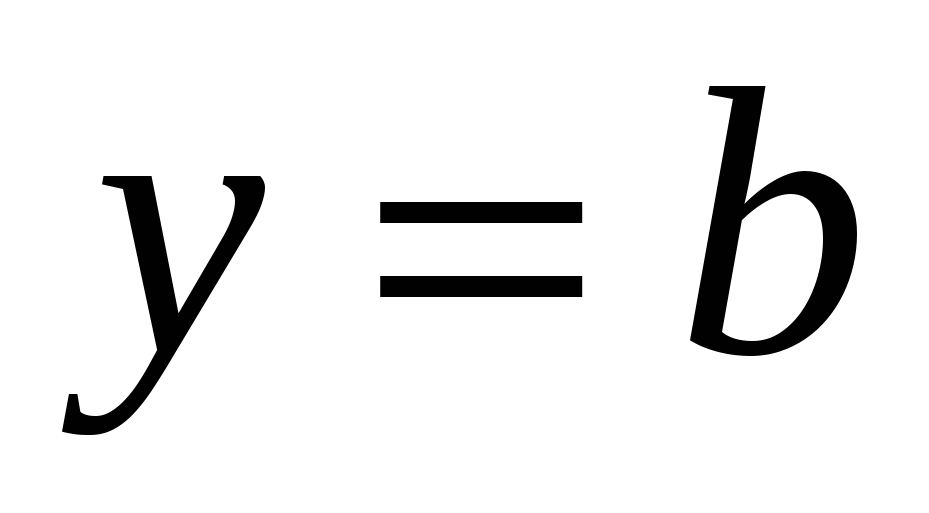 .)
.)
Обобщение и систематизация ранее изученного.
Слайд 2. Определите, какие функции являются линейными
-
Что является графиком линейной функции?
-
(Графиком линейной функции является прямая линия.)
-
Как построить график линейной функции?
-
(Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки в координатной плоскости и провести через них прямую.)
-
Почему для построения графика линейной функции достаточно только двух точек?
-
(Из начальных геометрических сведений мы знаем, что через две точки плоскости можно провести прямую линию и причем только одну.)
-
Что значит утверждение: «точка принадлежит графику функции»?
-
(Данное утверждение означает, что абсцисса этой точки равна аргументу, а ордината – соответствующему значению функции.)
Слайд 3. Представлены 5 графиков.
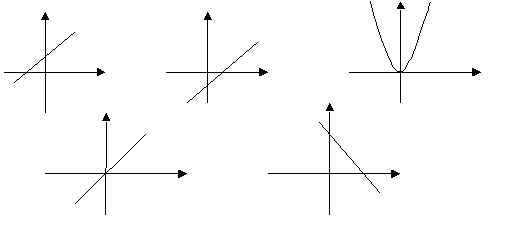
График какой функции лишний? Объяснить почему.
Слайд 4. На каком рисунке изображен график линейной функции у = kx? Ответ объяснить.
Слайд 5. На каком рисунке коэффициент k в уравнении линейной функции отрицателен? Ответ объяснить.
Слайд 6. На каком рисунке свободный член m в уравнении линейной функции отрицателен? Ответ объяснить.
С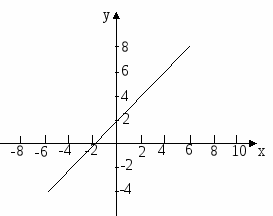
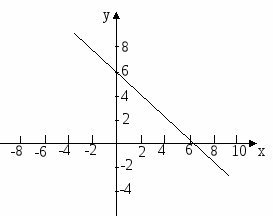 лайд 7. Составьте уравнения прямых, изображенных на этих рисунках.
лайд 7. Составьте уравнения прямых, изображенных на этих рисунках.
1. у = 2х; 2. у = х + 2; 3. у = -х + 2. 1. у = х + 6; 2. у = -6х; 3. у = -х + 6
Слайд 8. Представлены три графика:
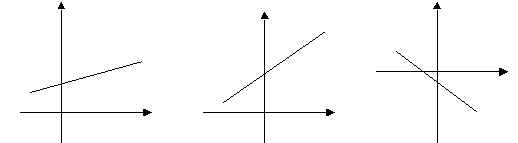
у = 0,5х + 2; у = 1,5х; у = - х – 1;
Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка? Ответ объяснить.
Слайд 9. На рисунке изображены графики функций:
у = 3х; у = - 3х; у = х – 3;
Под каким номером изображен график функции у = - 3х?
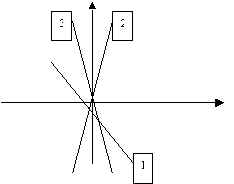
Слайд 10. Какие точки принадлежат графику линейной функции
у = - 0,5х + 1
а) А(-1;0); б) В(-2; 2,5); в) С(-2;0); г) Е(0;1)?
Слайд 11. При каком значении х значение функции у= - 0,5х +1 равно 5
а) х = 8; б) х = - 8; в) х = 9;
Слайд 12. Назвать функции, графики которых:
а) параллельны;
б) пересекаются в одной точке. Назвать эту точку.
в) совпадают.
1. у = - 2х – 1; у = - 2х + 5;
2. у = - 0,5х; у = 0,5х – 3;
3. у = - х – 4; у = -х – 4;
Слайд 13. Задать формулой функцию, график которой параллелен прямой у = - 8х + 11 и проходит через начало координат.
-
Исследовательская работа.
Следующим этапом нашей работы будет выполнение исследовательской работы. Вам предлагается в одной системе координат построить данные графики и ответить на предложенные вопросы.
1 вариант: В одной координатной плоскости построить графики функций: ![]() ;
; ![]() ;
; ![]() .
.
б) Ответить на вопросы: 1) Графики функций представляют собой… 2) Что общего в формулах этих функций? 3) В каких координатных четвертях проходят графики? 4) Каково значение коэффициента по знаку? 5) Опишите, каков угол наклона графиков функций к оси Ох. 6) Чему равна ордината точки пересечения графиков с осью Оу?
2 вариант: В одной координатной плоскости построить графики функций: ![]() ;
; ![]() ;
; ![]() .
.
б) Ответьте на вопросы: 1) Графики функций представляют собой… 2) В какой точке пересекаются графики функций? 3) Каково значение коэффициента по знаку? 4) Какой угол наклона каждого графика к оси Ох? 5) Каково соотношение между значениями коэффициента k и величинами углов наклона графиков к оси Ох?
( Выполняется работа в тетрадях, а два ученика с каждого варианта на доске цветными маркерами с последующей защитой своей работы)
-
Тестовая работа.
А теперь я предлагаю вам выполнить небольшой тест, а результаты его выполнения вы узнаете на следующем уроке.
| 1. Дана функция
0 -1,2 а) б)
1 1 х х в) г) 2 Подберите формулу, задающую эту функцию. а) б) в) г) |
-
Творческое задание.
Ребята, представьте себе, что вы составители учебника «Алгебра – 7».вам необходимо написать главу «Линейная функция». Отразите ваши знания в виде плана.
(Последующая проверка с дополнениями и коррекцией).
-
Подведение итогов.
-
Сформулируйте определение линейной функции.
-
Какие частные случаи линейной функции вам известны?
-
Что является графиком линейной функции?
-
Как построить график линейной функции?
-
Почему для построения графика линейной функции достаточно только двух точек?
-
Если коэффициенты у функций одинаковые, то графики функций – …
-
Если коэффициенты различны, то графики функций – …
-
Ордината точки пересечения графика функции с осью Оу равна …
-
Если коэффициент k > 0, то графики расположены в … координатных четвертях, углы наклона графиков функции к оси Ох – …
Если коэффициент k
-
Домашнее задание.
Дома вам предлагается завершить выполнение домашней контрольной работы №2 (стр. 62 по вариантам) и подготовиться к ее защите. Для этого вам понадобятся все знания, которые мы повторили и обобщили на сегодняшнем уроке «Бенефис линейной функции».
Здесь представлен конспект к уроку на тему «Бенефис линейной функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

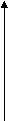
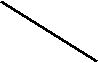
 1
1 
 0 х х
0 х х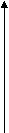
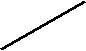
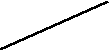

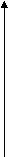 у
у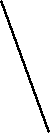 . Дан график функции
. Дан график функции 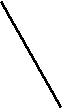
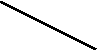
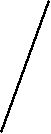 . Дан график функции
. Дан график функции 