Конспект урока «Функции. Тригонометрические функции» по математике



![]()
Учитель математики ГБОУ СОШ № 230 с углубленным изучением химии и биологии
Ваганова Г. В.
![]()
![]()
Тема :
« Функции. Тригонометрические функции »
(обобщающий урок, 2 часа)
Цели:
1) проверка и систематизация знаний учащихся по основным вопросам темы « Функции » и умения их применять к исследованию тригонометрической функции (нахождение области определения функции, области значений функции, периода функции, нечетность);
2) продолжить отработку умения учащихся исследовать функции в процессе выполнения лабораторно - практической работы;
3) организация работы учащихся в паре постоянного состава, что способствует более глубокому усвоению учебного материала ( ученик, проговаривая информацию, лучше ее усваивает), рождению интереса к процессу учения – выработка умения строить графики тригонометрических функций, используя свойства растяжения и сжатия их по координатным осям.
4) развивать умение анализировать, делать выводы и на их основе находить верные пути решения, память, грамотную математическую речь, развитие личности учащегося через самостоятельную творческую работу,
обеспечить устойчивую мотивационную среду, интерес к изучаемой теме;
5) воспитывать волю и настойчивость в достижении положительного результата в обучении, уверенность в собственных силах, чувство взаимопомощи, сотрудничества.
План-конспект:
I.Устный опрос и упражнения.
1. Что такое функция?
2. Способы задания функции.
3. Область определения функции.
4. Область значения функции.
Используя эти знания, ответьте на вопросы:
1) Для функции, графики которых изображены на рисунках, укажите область определения и область значения.
Презентация “Свойства функции”. Слайд 2.
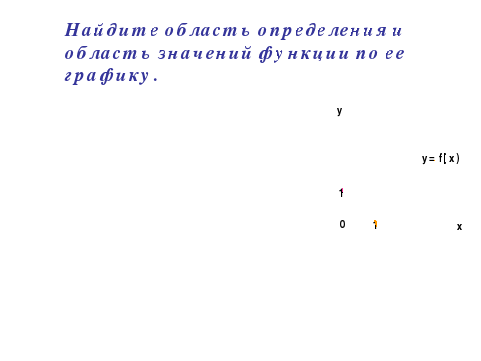
2) Найти область определения функции, заданной аналитически: Слайд 3.

5. Дайте определение функции, возрастающей на данном промежутке, убывающей на данном промежутке.
Используя эти определения, укажите промежутки возрастания и убывания функции: Слайд 2.
6. Дайте определение четной функции, нечетной
функции: Слайды 4,5,6.
1)

2)

3)Используя эти определения, укажите, какие из следующих функций являются четными, а какие –нечетными:
а) f( x ) = x/sinx
б) f ( x ) = x3cosx
в) f ( x ) = x2sinx
г)f ( x ) = ctgx/sinx
д) f ( x ) = x + sin x
е) f ( x ) = x2 + x tgx
2) Исследуйте функции на четность и нечетность:

7. Какая функция называется периодической?
Назовите наименьший положительный период функции: Слайд 7
y = 2sin 2x
y = 2cos 4x
y = tg2x
y = sin![]()
y = cos![]()
y = sin![]() + tgx
+ tgx
y = sin2x + cosx
II. Самостоятельная работа №1 по теме:
“Область определения, область значений, период, четность и нечетность тригонометрической функции”.
с самопроверкой, используя готовые ответы (ответы – на карточке партнера).
Задания с.р. дифференцированы.
1-4 варианты – для сильных учащихся;
2-8 варианты – для слабых учащихся;
9-12 варианты – для среднего ученика.
Самостоятельная работа .
I. 1.Найдите область определения функции:
y = ![]()
2. Найти область значений функции:
y = sinx + sin( x+ ![]() )
)
3. Найти период функции:
y = cos![]() + tg
+ tg![]()
4. Определить , является ли данная функция четной или нечетной:
y = |x| + cosx
II. 1. y = ![]()
-
y = 10cos2x - 6sinxcosx + 2sin2x
-
y = tg
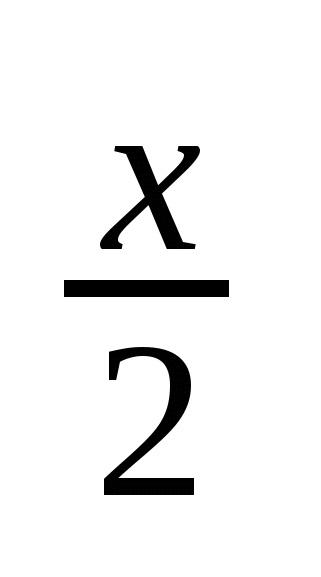 + sin
+ sin 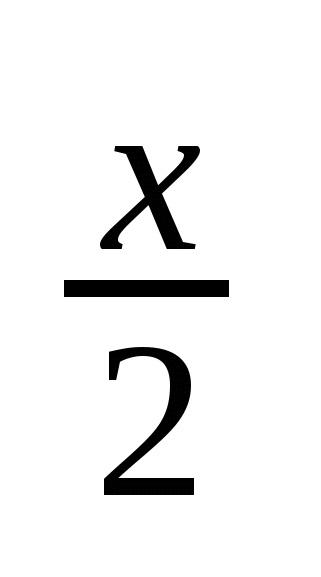 + cos3x
+ cos3x -
y =
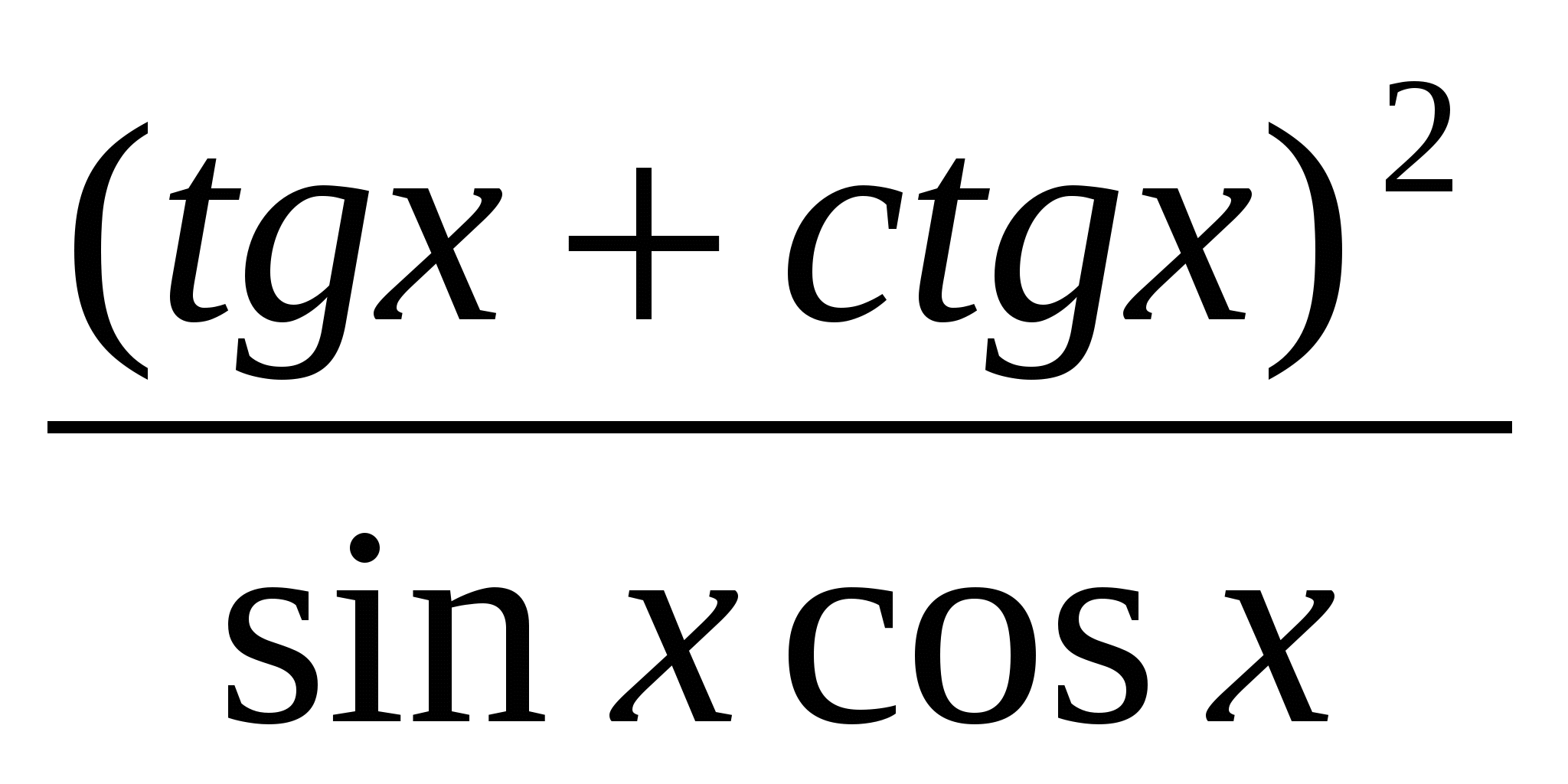
III. 1. y = 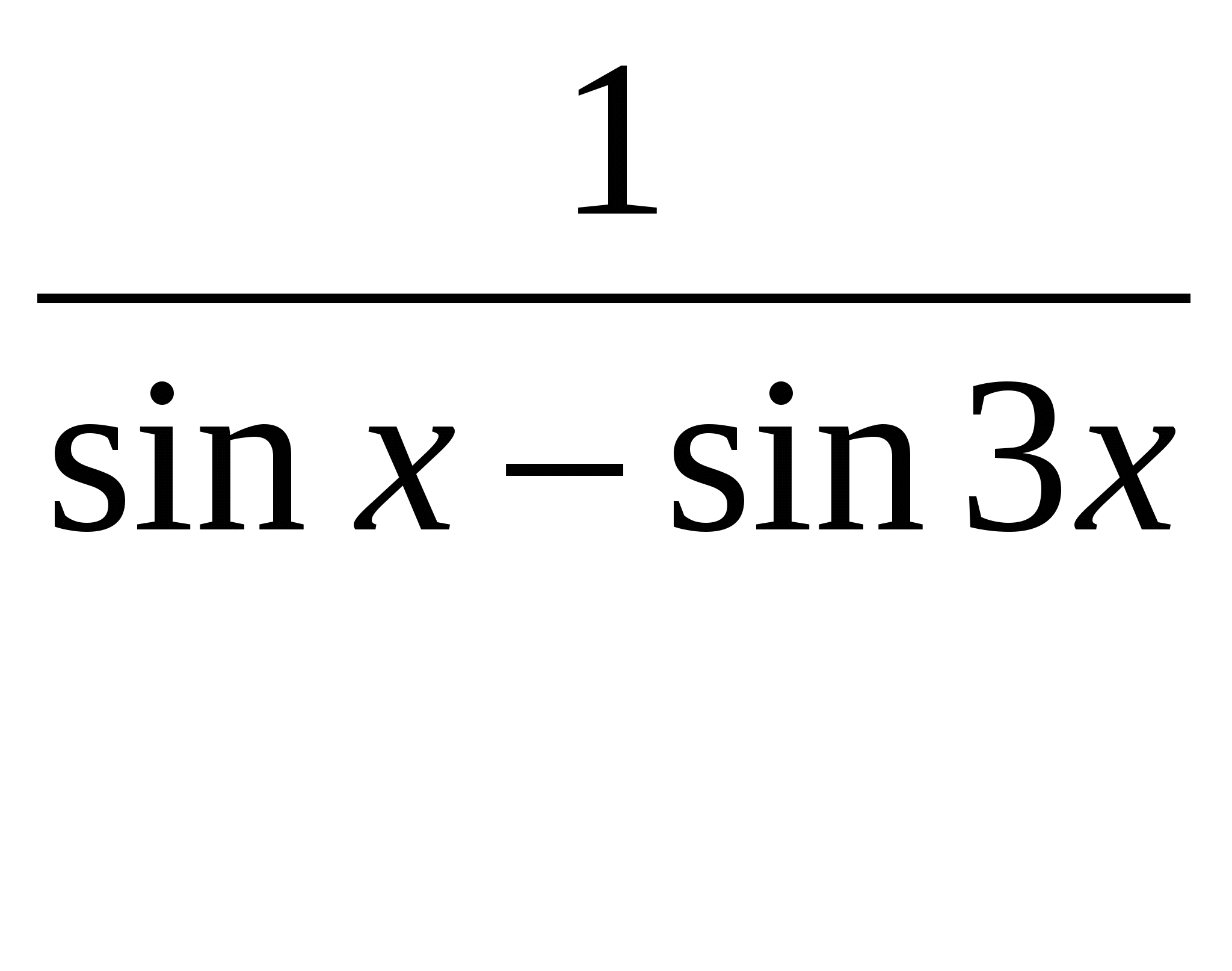
2. y = 3cos2x - 4sin2x
3. y = sin![]() + 5cos
+ 5cos ![]()
4. y = (x2+1)sinx
IV. 1. y = ![]()
2. y = 7sinx + 4cosx
3. y = 2ctg3x - 4tg2x
4. y = ![]()
V. 1. y = ![]()
2. y = 2 sinx
3. y = sin2x
4. y = sinx3
VI. 1. y = ![]()
2. y = 3cosx
3. y = tg2x
4. y= sinx2
VII. 1. y = ![]()
2. y = 2sinx - 1
3. y = cos![]()
4. y = tg5x
VIII. 1. y = ![]()
2. y = 3cosx + 1
3. y = sin![]()
4. y = sin |x|
-
1. y =
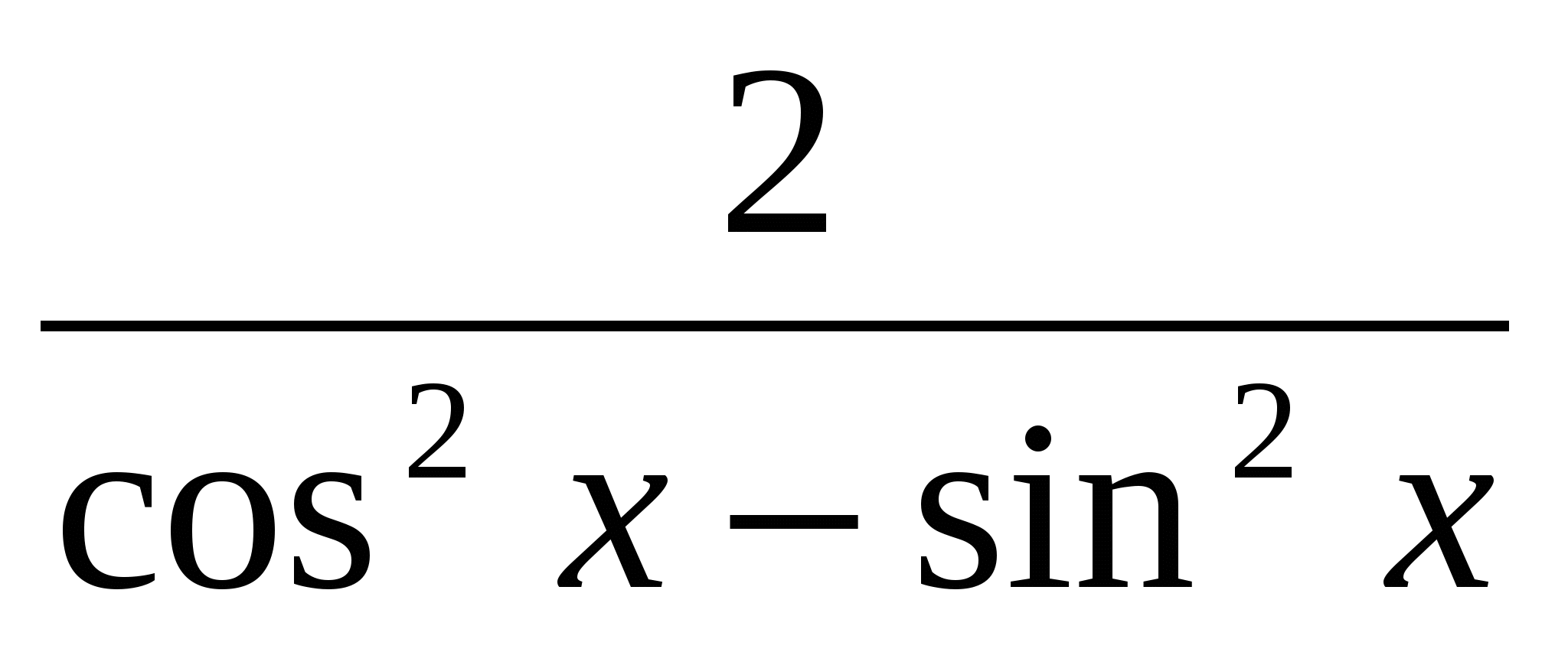
2. y = 2sin![]() + 1
+ 1
3. y = cos3x
4. y = xsinx
-
1. y =
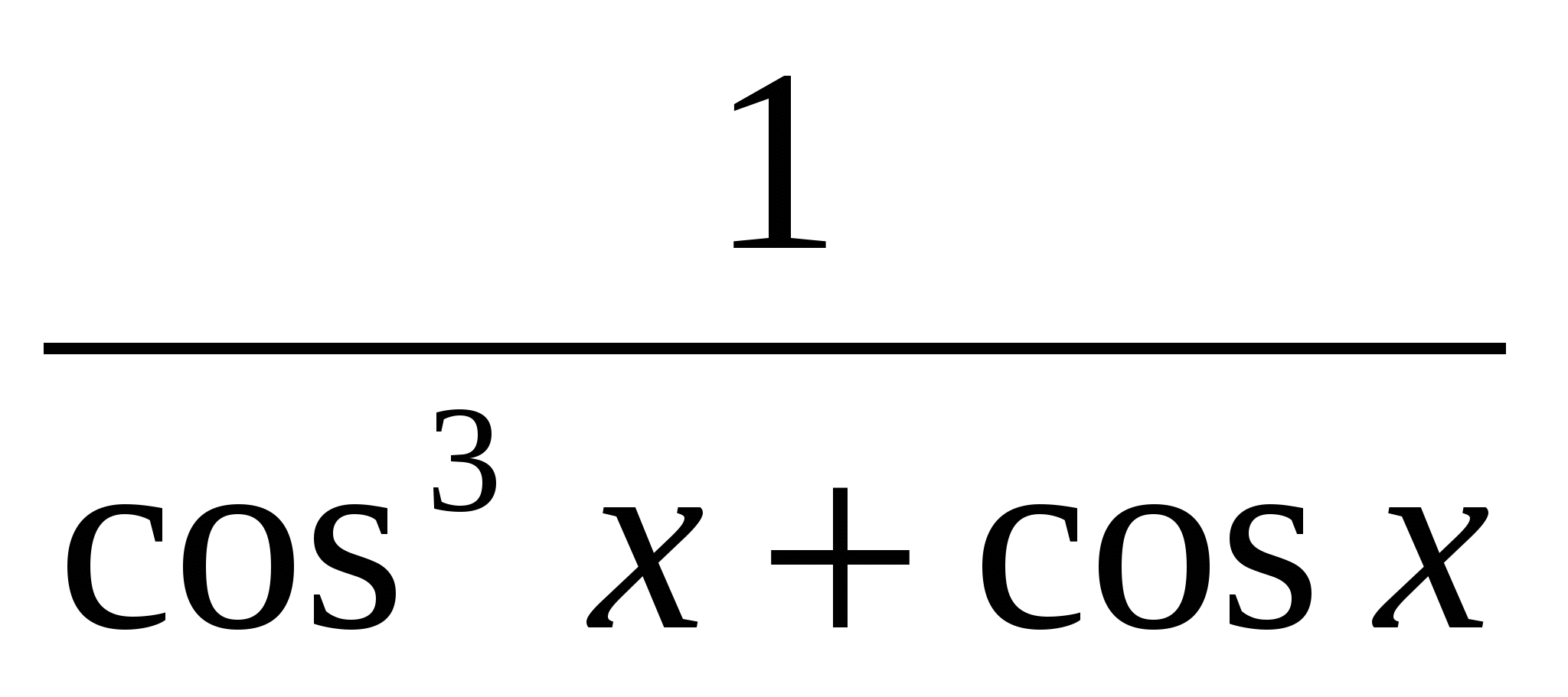
2. y = 2cos ![]() - 1
- 1
3. y = sinx + tgx
4. y = x2cos2x
-
1. y =
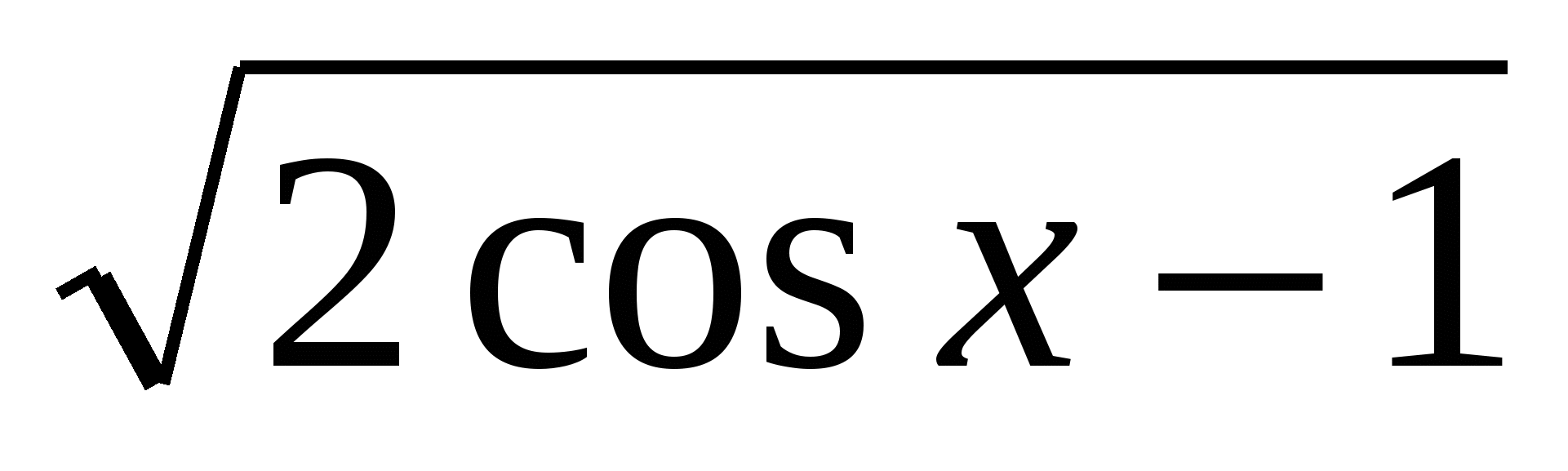
2. y = 2cos2x+5
3. y = sin![]()
4. y = x + sinx
-
1. y =
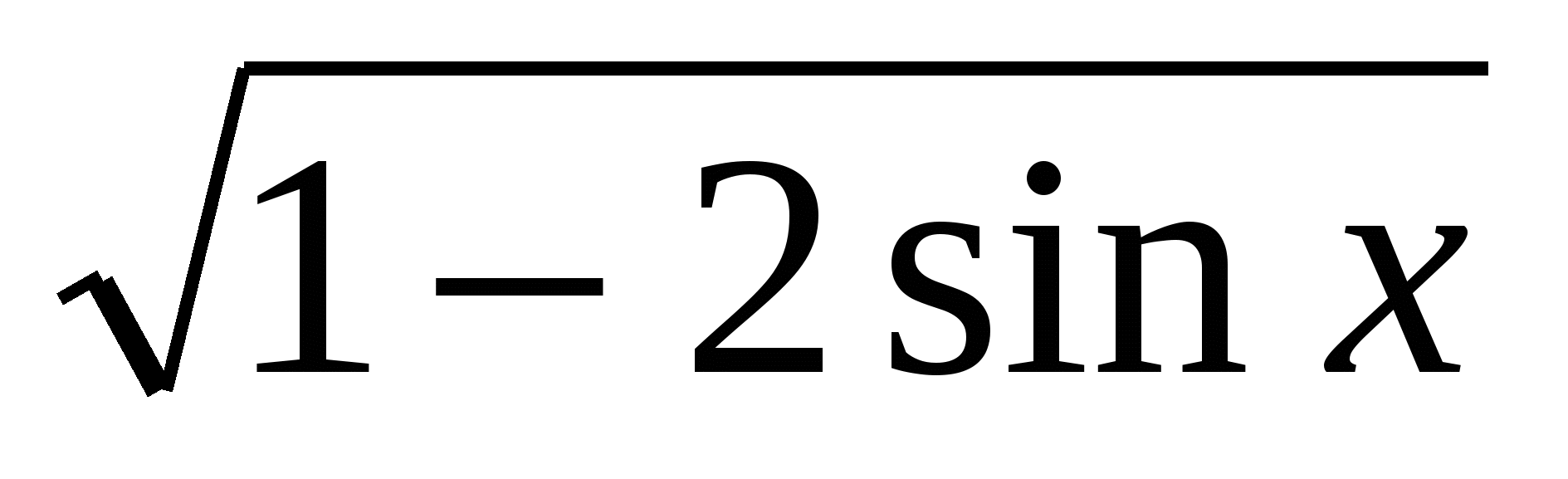
2. y = cos2xcosx + sin2xsinx - 3
3. y = tg5x
4. y = x + cosx
-
Лабораторно-практическая работа по теме «Функция »
Источник: Л.И. Звавич и др. « Контрольные и проверочные работы по алгебре, 10-11 кл.» М., « Дрофа », 1996, с. 11-12
Дана функция y = f(x)
1) Найдите по графику:
а) f(3); f(-1); f(5);
б) значения x , при которых f(x)=1.
2) исследуйте функцию.
Работа проводится по 8 вариантам.
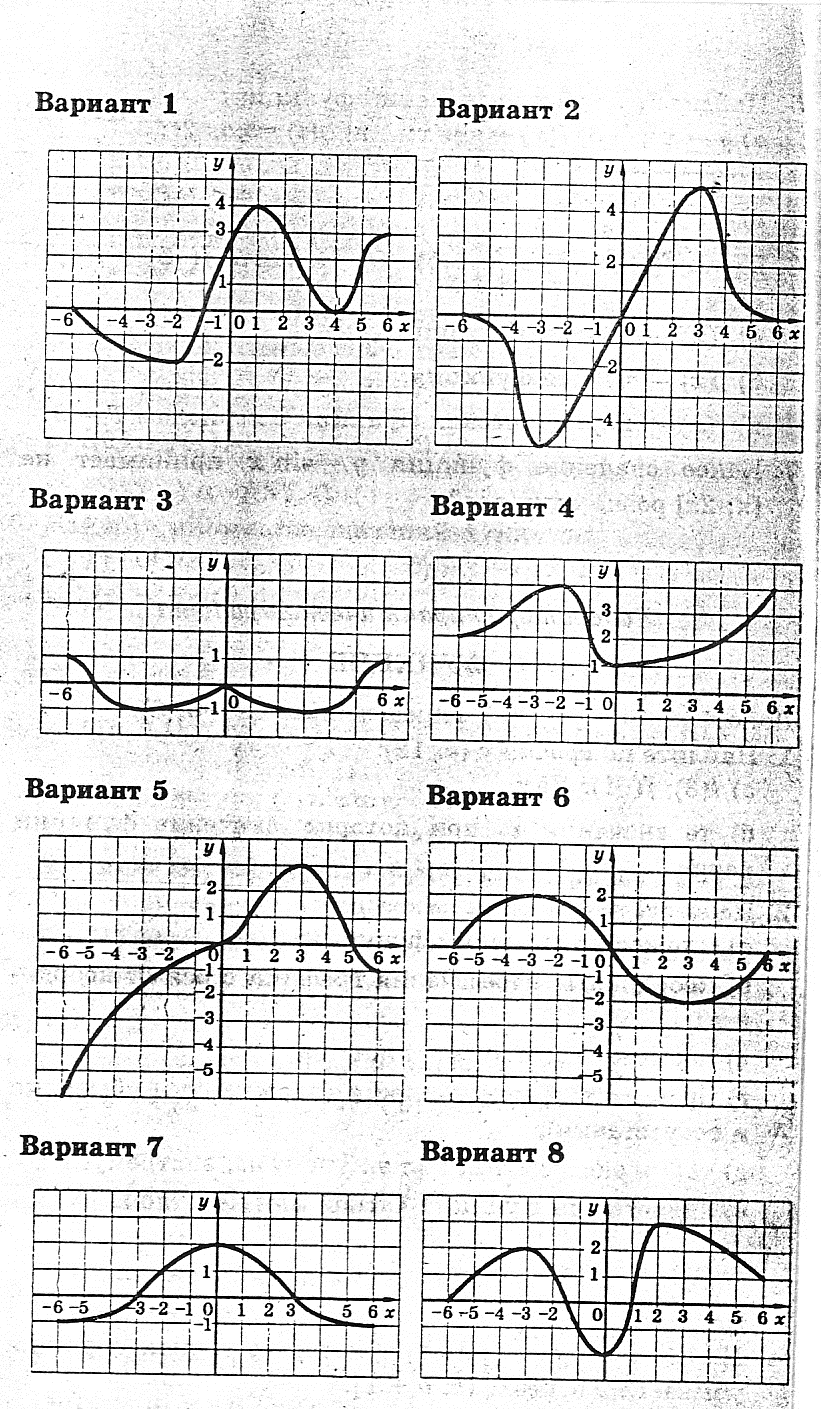
Каждому ученику - отдельный лист с одним вариантом
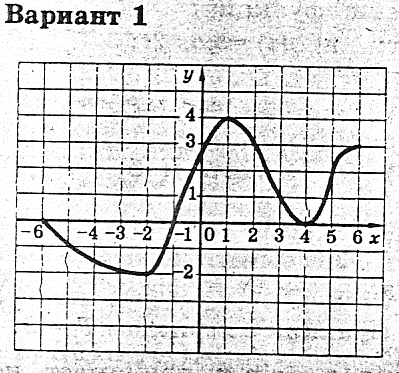
Лабораторно – практическая работа.
-
Найдите по графику:
а) f (3) = ; f (- 1) = ; f (5) = .
б) значения х, при которых f( x) = 1.
2. Исследуйте функцию по плану:
1) D (y):
2) E (y):
3) y = 0 при x =
y > 0 при x ![]()
y x ![]()
4) y возрастает при x ![]()
y убывает при x ![]()
5) Четность – нечетность:
6) y наибольшее = при x =
y наименьшее = при x =
IV. Построение графиков гармонических колебаний, используя приемы растяжения, сжатия, смещения по осям координат.
1. Повторить приемы построения графиков гармонических колебаний.
y = kf(x)
y = f(x) + b
y = f(x – a)
y = f(mx)
А с преобразованиями вида y = |f(x)|и y = f(|x|) вы познакомитесь, работая в парах.
Задание: По заданным графикам определите вид функции.

Самостоятельная работа№2 по вариантам ( проверка учителем)
-
y = 2 cos(
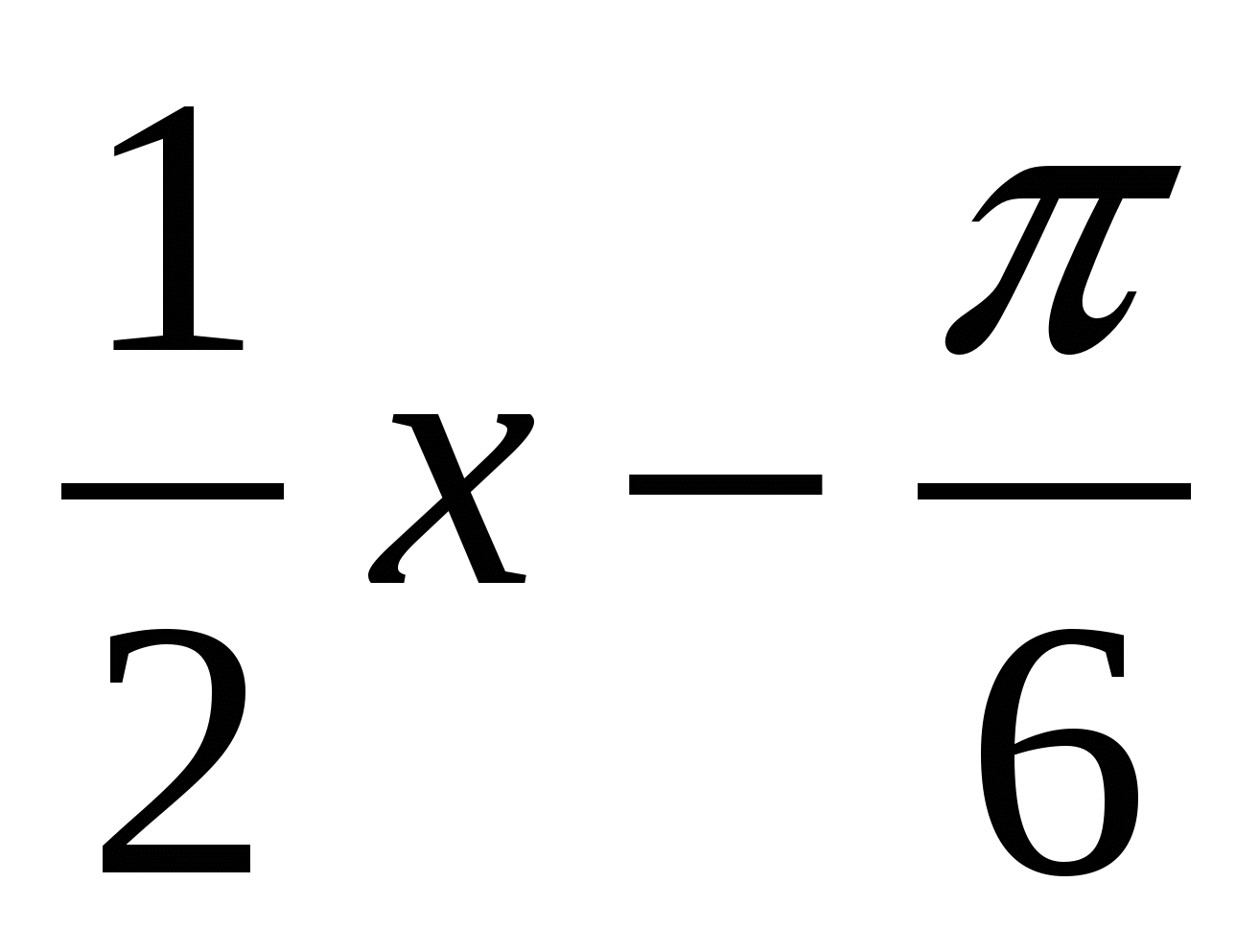 )+1
)+1 -
y = - sin (2x +
 )-2.
)-2.
V. Работа в парах постоянного состава. Построение графиков тригонометрических функций, содержащих модуль.
1 вариант: y = |sin x|
2 вариант: y = sin|x|
Решение: 1) y = |sin x|
Отображение нижней части графика функции
y = f(x) в верхнюю полуплоскость относительно оси абцисс с сохранением верхней части графика.
Или
Для построения графиков данных функций используем правило раскрытия модуля:
|a| =
1) a, если a ≥ 0
2) –a,если а
а) если sinx ≥ 0, то y = sinx
б) если sinx y = -sinx
- Строим график функции y = sinx и обводим только ту его часть, где y ≥ 0.
- Строим график функции y = -sinx ( в той же системе координат) и обводим ту его часть, где y > 0.
2) y = sin |x|
а) если x ≥ 0, то y = sinx,
б) если x y = -sinx.
- Строим график функции y = sinx и обводим только ту его часть, где x ≥ 0.
- Строим график функции y = -sinx и обводим ту его часть, где x
Или
Отображение правой части графика функции y = f(x)
в левую полуплоскость относительно оси ординат с сохранением правой части графика.
V. Результат работы в парах. С. р. №3 с взаимопроверкой.
Построить график функции:
I вариант. y = sinx + |sinx|
II вариант. y = 2sinx|cosx|
-
y = sinx + |sinx|
а) sinx ≥ 0; y = 2sinx
б) sinx
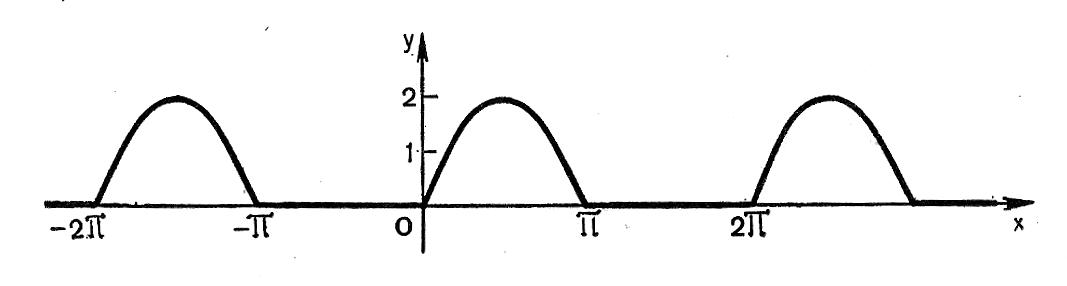
-
y = 2sinx|cosx|
а) cosx ≥ 0; y = 2sinxcosx= sin2x
б) cosx
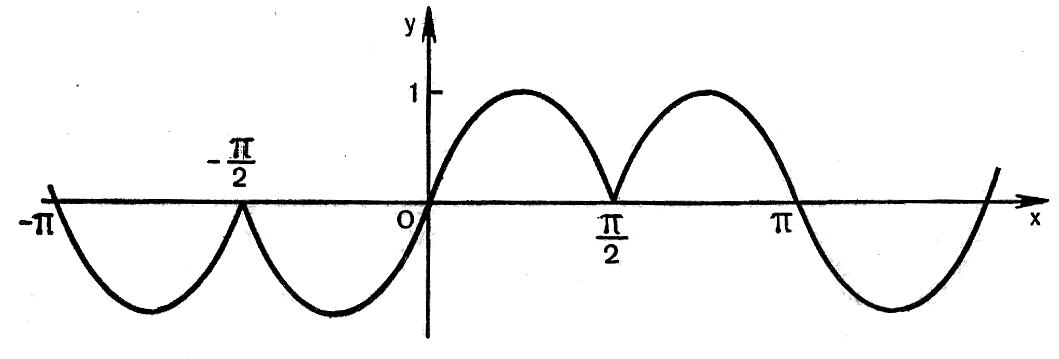
VI. Заключение: подведение итогов по различным этапам урока, выставление оценок.
-
устная работа;
-
С.р. № 1 ( D(y); E(y); T; четность - нечетность);
-
С.р. № 2 ( построение графиков гармонических колебаний);
-
Лабораторно – практическая работа;
-
Работа в парах постоянного состава;
-
С. р. №3 (построение графиков функций, содержащих модули).
-
Самоанализ и самооценка.
-
Рефлексия.
Ф. И. О._____________________________________
Самоанализ и самооценка по следующим критериям:
-
Качество выполнения мною первой самостоятельной работы ________________________
-
Качество выполнения мною второй самостоятельной работы (построение графиков гармонических колебаний)_________________________
-
Качество объяснения своей темы ученику В (об этом может свидетельствовать количество задаваемых вопросов учеником В по ходу объяснения, а также качество третьей самостоятельной работы, выполненной учеником В)_________________________
-
Качество третьей самостоятельной работы, выполненной мною______________________
-
Уровень моей самостоятельности при выполнении третьей самостоятельной работы____________________
Рефлексия (по 10-балльной шкале)
- Я хорошо себя чувствовал(а), мне было интересно, у меня все получилось ____
- Я испытывал(а) затруднения, волнение, у меня не все получилось так, как я хотел(а) бы_______________
- Мне было неуютно, неинтересно (если возможно, укажите причину)______________________________________
Лабораторно – практическая работа.
-
Найдите по графику:
а) f (3) = ; f (- 1) = ; f (5) = .
б)значения х, при которых f( x) = 1.
2. Исследуйте функцию по плану:
1) D (y) :
2) E (y):
3) у = 0 при х =
у > 0 при х ∈
у
4) у возрастает при х ∈
у убывает при х ∈
5) Четность – нечетность:
6) у наибольшее = при х = ;
У наименьшее = при х = .
Литература
1. “Устные упражнения по алгебре и начала анализа”.
Р.Д. Лукин, Т.К. Лукина, М.С. Якунина, М., Просвещение, 1989
2. Л.И. Звавич, Л.Я. Шляпочник. “Контрольные работы и проверочные по алгебре , 10-11 кл.”. М., Дрофа, 1996
3. В.С. Крамор “Повторяем и систематизируем школьный курс алгебры и начал анализа”.
М., Просвещение, 1990
4. Алгебра и начала анализа. Учебник для 10-11 кл.,
Ш.А. Алимов и др., М., Просвещение , 2011
5. Алгебра и начала анализа. Учебник для 10-11 кл.,
А.Н. Колмогоров и др., М., Просвещение, 2009
Здесь представлен конспект к уроку на тему «Функции. Тригонометрические функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

