Экзаменационная работа по математике за
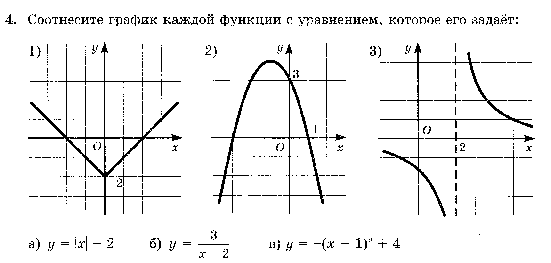
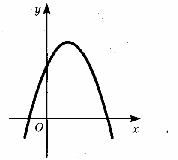
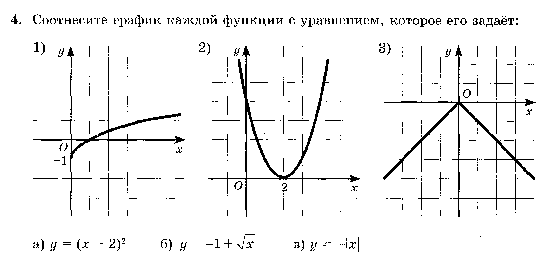
Вариант 1
Часть 1
1. Запишите в порядке возрастания числа, используемые в тексте.
Масса планеты Юпитер равна 1,9 • 1027 кг, планеты Уран — 8,69 • 1025 кг, планеты Сатурн — 5,68 • 1026 кг, а планеты Нептун — 1,02 • 1026 кг.
а)1,02*1026; 1,9 • 1027; 5,68 • 1026; 8,69 • 1025
б)5,68*1026; 8,69 • 1025; 1,9 • 1027; 1,02 • 1026
в)8,69*1025; 5,68 • 1026; 1,9 • 1027; 1,02 • 1026
г) 8,69 • 1025; 1,02 • 1026; 5,68 • 1026; 1,9 • 1027
2.В каком случае преобразование выполнено, верно?:
1)3(х - у) = 3х-у 2)(3+х)(х-3)=9 - х2
3)(х - у)2=х2-у2 4)(х+3)2= х2+6х+9
3. Решите уравнение: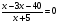
5.Найдите меньший корень уравнения: 5х2- 7х + 2 = 0
6.Вычислите: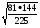
7. Укажите уравнение, которое является математической моделью данной ситуации: «Катер прошёл 6 км против течения реки и 8 км по течению, затратив на весь путь 1,2 ч. Найдите собственную скорость катера х км/ч, если скорость течения реки равна 3 км/ч».
а) 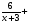
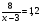 в)
в)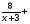
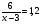
б) 6(х - 3) + 8(х + 3) = 1,2 г) 8(х - 3) + 6(х + 3) = 1,2
8. Высота камня, подброшенного вертикально вверх, изменяется по закону h(t) = 6t - t2, где t — время в секундах, h — высота в метрах. Сколько секунд тело будет находиться на высоте более 8 м?
9.Гипотенуза прямоугольного треугольника равна 3 см, а один из катетов равен 1 см. Найдите длину (в см) другого катета. Ответ запишите в виде десятичной дроби. Округлив до десятых.
10.Пусть (х;у)-решение системы уравнений: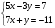 .Найдите х+у
.Найдите х+у
11.Решите неравенство: х-2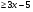
а)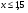 б)
б)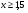 в)
в)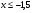 г)
г)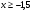
12.Из формулы объема цилиндра V= 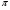 R2h выразите R.
R2h выразите R.
a) R=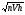 б) R=
б) R=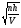 в) R=
в) R=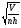 г) R=
г) R=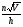
Часть 2
13. Упростите выражение:
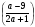 *
*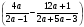 =
=
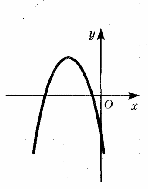
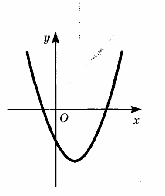
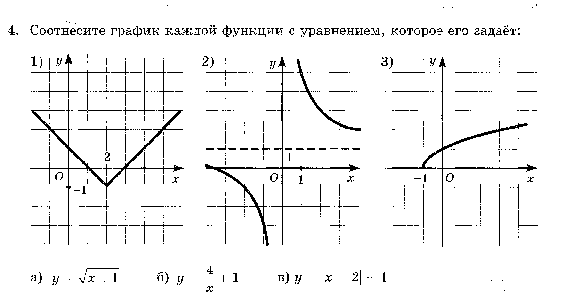
14.По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b, с.
15.Решить задачу:Из города А в город В, расстояние между которыми 300 км, выехал автомобиль, а одновременно с ним из пнкта В выехал другой автомобиль со скоростью на 20 км/ч больше.Через 3 часа они встретились.Найдите скорости,с которыми двигались автомобили(в км/ч).
Вариант 2
Часть 1
1. Запишите в порядке убывания числа, используемые в тексте.
Масса планеты Земля равна 6 • 1024 кг, планеты Марс — 6,4 • 1023 кг, планеты Венера — 4,9 • 1024 кг, а планеты Нептун — 1,02 • 1026 кг.
а)1,02 1026; 4,9 • 1024; 6 • 1024; 6,4 • 1023 в)6,4
1026; 4,9 • 1024; 6 • 1024; 6,4 • 1023 в)6,4 1023; 4,9
1023; 4,9 1024; 6 • 1024; 1,02 • 1026 б) 4,9 • 1024; 6 • 1024; 6,4 • 1023; 1,02 • 1026 г)1,02
1024; 6 • 1024; 1,02 • 1026 б) 4,9 • 1024; 6 • 1024; 6,4 • 1023; 1,02 • 1026 г)1,02 1026; 6 • 1024; 4,9 • 1024; 6,4 • 1023
1026; 6 • 1024; 4,9 • 1024; 6,4 • 1023
2.В каком случае преобразование выполнено, верно?:
1)2(5x-1)=10x-1 2)(y-x)(y+x)=x2+y2
3)(x-3)2=x2-9 4)(y-5)2=y2-10y+25
3. Решите уравнение: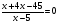
5. Найдите наибольший корень уравнения:5х2+21х +4=0
6. Вычислите: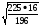 =
=
7. Укажите уравнение, которое является математической моделью данной ситуации: «Моторная лодка прошла 10 км по течению реки и 12 км против течения, затратив на весь путь 2 ч 20 мин. Найдите скорость течения реки х км/ч, если собственная скорость лодки равна 10 км/ч».
а)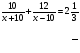 в)
в)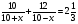
б)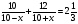 г)10(10+х)+12(10-х)=2
г)10(10+х)+12(10-х)=2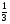
8. Высота мяча, подброшенного вертикально вверх, изменяется по закону h(t)=1+5t-t2, где t — время в секундах, h — высота в метрах. Сколько секунд тело будет находиться на высоте более 5 м?
9. Длина диагонали квадрата равна 5 см. Найдите длину стороны этого квадрата. Ответ запишите в виде десятичной дроби, округлив ее до десятых.
10. .Пусть (х;у)-решение системы уравнений: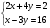
 .Найдите х+у
.Найдите х+у
11.Решите неравенство: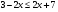
а)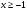 б)
б)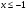 в)
в)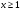 г)
г)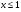
12.Из формулы площади круга S = 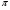 R2 выразите R.
R2 выразите R.
а)R=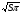 б)R=
б)R=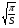 в)R=
в)R=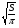 г)R=
г)R=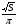
Часть 2
13.Упростите выражение: 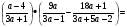
14. По графику функции у = ах2 + вх + с определите знаки коэффициентов а, в, с.
15.Решите задачу: Прогулочный теплоход по течению реки проплывает 12 км за такое же время, что и 10 км против течения. Найдите скорость течения реки, если собственная скорость теплохода 22 км/ч.
Вариант 3
Часть 1
1. Запишите в порядке возрастания числа, используемые в тексте.
Население Австралии составляет 1,83 107 человек, население Индонезии — 1,98
107 человек, население Индонезии — 1,98 108 человек, Малайзии — 20,4
108 человек, Малайзии — 20,4 106 человек, а Индии — 0,95 • 109 человек.
106 человек, а Индии — 0,95 • 109 человек.
а)1,83 107; 20,4 • 106; 1,98 • 108; 0,95 • 109
107; 20,4 • 106; 1,98 • 108; 0,95 • 109
б)0,95 109; 1,83 • 107; 1,98 • 108; 20,4 • 10е
109; 1,83 • 107; 1,98 • 108; 20,4 • 10е
в)0,95 109; 1,98
109; 1,98 108; 20,4 • 106; 1,83 • 107
108; 20,4 • 106; 1,83 • 107
г)1,83 107; 1,98 • 108; 20,4 • 106; 0,95 • 109
107; 1,98 • 108; 20,4 • 106; 0,95 • 109
2.В каком случае преобразование выполнено, верно?:
а)8(х -у)= х - 8у б)( а -в)2= а2-в2 в)(8+у)2= 64 -16у+у2 г)(5+у)2= 25+10у+у2
3. Решите уравнение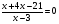
5.Найдите наименьший корень уравнения:3х2 +5х – 2=0
6. Вычислите: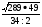 =
=
7. Укажите уравнение, которое является математической моделью данной ситуации: «Катер прошёл по течению реки 6 км, а против течения — 10 км, затратив при этом на путь против течения на 45 мин больше, чем на путь по течению. Найдите скорость течения реки х км/ч, если собственная скорость катера равна 10 км/ч»
а) 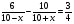 в)
в)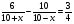
б)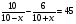 г)
г)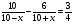
8. Высота тела, подброшенного вертикально вверх, изменяется по закону h(t) = 7t – 2t2, где t — время в секундах, h — высота в метрах. Сколько секунд тело будет находиться на высоте более 3 м?
9. Стороны прямоугольника 4 см и 5 см. Найдите длину его диагонали. Ответ запишите в виде десятичной дроби, округлив ее до десятых.
10.Пусть (х;у)-решение системы уравнений: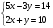 Найдите х-у.
Найдите х-у.
11.Решите неравенство: 5х-7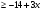
12.Из формулы дискриминанта Д=в2-4ас, выразите в:
а) в =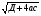 б)в =
б)в =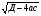 в) в =
в) в =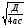 г) в =
г) в =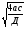
Часть 2
13.Упростите выражение:
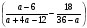
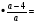
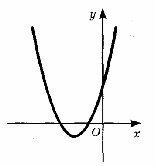
14. По графику функции у = ах2 + вх + с определите знаки коэффициентов а, в, с.
15.Решить задачу:Туристы проплыли на лодке по озеру 18 км за такое же время, что и 15 км против течения реки,впадающей в озеро.Найдите скорость движения лодки по озеру,если скорость течения реки 2 км/ч.
Вариант 4
Часть 1
1. Запишите в порядке убывания числа, используемые в тексте.
В состав Российской Федерации входит ряд республик. Из них Республика Тува занимает площадь 1,7 • 105 км2, Республика Саха — 3,1 • 106 км2, Республика Татарстан — 6,8 • 104 км2, а Республика Башкортостан — 1,44-105км2.
а)1,44 105; 1,7
105; 1,7 105; 3,1 • 106; 6,8 • 104
105; 3,1 • 106; 6,8 • 104
б)6,8 104; 1,44 • 105; 1,7
104; 1,44 • 105; 1,7 105; 3,1 •106
105; 3,1 •106
в)3,1 106; 1,7
106; 1,7 105; 1,44 • 105; 6,8 • 104
105; 1,44 • 105; 6,8 • 104
г)6,8 104; 3,1
104; 3,1 106; 1,7 • 105; 1,44 • 105
106; 1,7 • 105; 1,44 • 105
2. В каком случае преобразование выполнено, верно?:
а) ( а - в)2=(а - в) (а + в) в) (а + в)2= а2+ ав+ в2
б) (а - в)2= (а2- 2ав + в2) г) (а + в)(а - в)=(а - в)
3. Решите уравнение: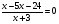
5. Найдите наибольший корень уравнения: х2-7х+10 =0
6.Вычислите: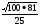
7. Укажите уравнение, которое является математической моделью данной ситуации: «Моторная лодка проплыла против течения реки 12 км и по течению реки 10 км, затратив на путь по течению на 40 мин меньше, чем на путь против течения. Найдите собственную скорость лодки км/ч, если скорость течения реки равна 3 км/ч.»
а)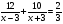 б)
б)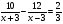
в)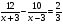 г)
г)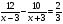
8. Высота тела, подброшенного вертикально вверх, изменяется по закону h(t) = 1 + 9t – 2t2, где t— время в секундах, h — высота в метрах. Сколько секунд тело будет находиться на высоте более 5 м?
9.Сторона квадрата равна 3см. Найдите длину(в см) диагонали этого квадрата. Ответ запишите в виде десятичной дроби, округлив до десятых.
10.Пусть (х;у)-решение системы уравнений: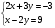 Найдите
Найдите 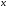
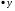
11.Решите неравенство: 4(х+7) 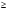 6х-12
6х-12
12.Из формулы нахождения стороны правильного треугольника 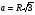 выразите R.
выразите R.
а)R =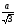 б)R=
б)R=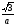 в)R=
в)R=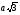
Часть 2
13. Упростите выражение:
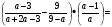
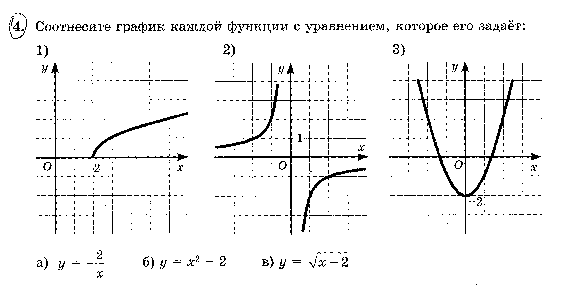
14. По графику функции у = ах2 + вх + с определите знаки коэффициентов а, в, с.
15.Решите задачу:Расстояние между пристанями 40км.Теплоход проплывает от одной пристани до другой и возвращается обратно за 3 ч 40 мин.Найдите скорость течения реки, если собственная скорость теплохода 22 км/ч.
Варианты контрольных измерительных материалов для проведения промежуточной аттестации по математике в 8-х классах общеобразовательных учреждений.
Инструкция по выполнению работы
На выполнение экзаменационной работы отводится 90 минут.Работа состоит из двух частей.Первая часть содержит 12 заданий базового уровня сложности,вторая часть 3 задания повышенного уровня сложности.
Решения всех задач экзаменационной работы (первой и второй частей) и ответы к ним записываются на отдельных листах.
Формулировки заданий не переписываются,рисунки не перечерчиваются.При записи ответа к заданию учитывается следующее:
-
в заданиях с выбором ответа указывается номер верного ответа
-
в заданиях с кратким ответом указывается число(целое число или десятичная дробь),получившееся в результате решения.
Все необходимые вычисления,преобразования производятся в черновике.Черновики проверяются ,но не учитываются при выставлении отметки.
Правильный ответ в зависимости от сложности каждого задания оценивается одним баллом.Баллы полученные за все выполненные задания,суммируются.
Желаем успеха!
Использованная литература:
-
Алгебра, учебник для 8 класса общеобразовательных учреждений / А.Г. Мордкович
-
Алгебра, задачник для 8 класса общеобразовательных учреждений / А.Г. Мордкович
-
Алгебра 7 – 9. Методическое пособие для учителя. / Мордкович А.Г.
-
Алгебра, 8 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова: Мнемозина, 2009.
5.Алгебра .8 класс.Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений(Л.А.Александрова под.редА.Г.Мордковича изд.Мнемозина)
6.Алгебра.Тематические тесты.8 класс.Промежуточная аттестация.(под.ред.Ф.Ф.Лысенко,С.Ю,Кулабухова)
Всего 15 заданий каждое задание оценивается одним баллом, всего 15 баллов.
Оценка: «2» менее 5 баллов
«3» 5-7 баллов
«4» 8-12 баллов
«5» 13-15 баллов
Ответы:
1 вариант 2 вариант
1.г 1.г
2.4 2.4
3.х=8 3.х=-9
4.1-в 4.1-г
2-а 2-б
3-б 3-в
5.0,4 5.-0,2
6.7,2 6.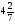
7.в 7.в
8.2или4 8.1или4
9.2,9 9.3,5
10. .(-1;-4) 10.(7;-3)
11.а 11.а
12.в 12.в
Здесь представлены материалы теста на тему «Экзаменационная работа по математике за », которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Математика (8 класс). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

