Олимпиадная работа по математике

Олимпиадная работа по математике в 7 классе

Куст Анжела Эдвардовна

учитель математики

МБОУ гимназии г. Гурьевска

Гурьевского района Калининградской области

Олимпиадные задания по математике

7 класс

1. Расставьте знаки действий «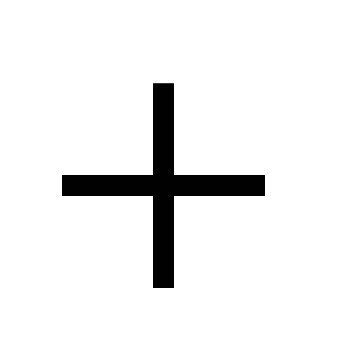», «–», «», «:» и скобки, чтобы получить верное равенство: (7 баллов)

а) 1999 = 0, б) 1999 = 1,

в) 1999 = 3, г) 1999 = 9,

д) 1999 = 10.

2. На доске написано число 321321321321. Какие цифры необходимо стереть, чтобы получить возможное наибольшее число, делящееся на 9?

(7 баллов)

3. Цифру 9, с которой начинается трёхзначное число, перенесли в конец числа. В результате получилось число на 216 меньше данного. Какое число было первоначально? (7 баллов)

4. Есть двое песочных часов: на 7 минут и на 11 минут. Яйцо должно вариться 15 минут. Как сварить яйцо, переворачивая часы минимальное число раз? (7 баллов)

5. В США дату принято записывать так: номер месяца, потом номер дня и год. В Европе же сначала идёт число, потом месяц и год. Сколько в году дней, дату которых нельзя прочитать однозначно, не зная, каким способом она написана? (7 баллов)

Максимальное количество набранных баллов – 35.

Решения олимпиадных задач

1. а) б)

в) г)

д)

2. Из признака делимости на 9 следует, что сумма стёртых цифр должна быть

равна 6. Так как больше то число, у которого цифр больше, то стирать надо

две тройки. Останется число из 10 цифр. Чтобы это число было наибольшим, надо в старших разрядах иметь большие цифры, поэтому стираем 2 последние тройки.

3. Обозначим вторую и третью цифры трёхзначного числа за x и y, тогда первоначальное число будет иметь вид: . После переноса цифры «9» в конец числа число будет иметь вид: . Учитывая, что разность чисел равна 216, после упрощения имеем: . Разделив обе части на 9, имеем . Учитывая, что , получим .

Ответ: 975.

4. Одновременно пустим те и другие часы. Когда пройдёт 7 минут, начнём варить яйцо. Через 4 минуты 11-минутные часы остановятся. Перевернём их и будем варить яйцо ещё 11 минут.

5. Очевидно, это те дни, у которых дата может быть номером месяца, т.е. принимает значения от 1 до 12. Таких дней . Но те дни, у которых число совпадает с номером месяца, понимаются однозначно. Таких дней 12. Поэтому искомых дней .

Список использованной литературы

1. Агаханов Н.Х., Терешин Д.А., Кузнецова Г.М. Школьные математические

олимпиады. – М.: Дрофа, 1999.

2. Горбачёв Н.В. Сборник олимпиадных задач по математике. – М.: МЦНМО,

2004.

3. Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады.

6 – 11 классы. – М.: Просвещение, 2010.