Презентация "Логика и дискретная математика" – проект, доклад

ЛОГИКА И ДИСКРЕТНАЯ МАТЕМАТИКА

Доцент Свертилова Наталья Викторовна

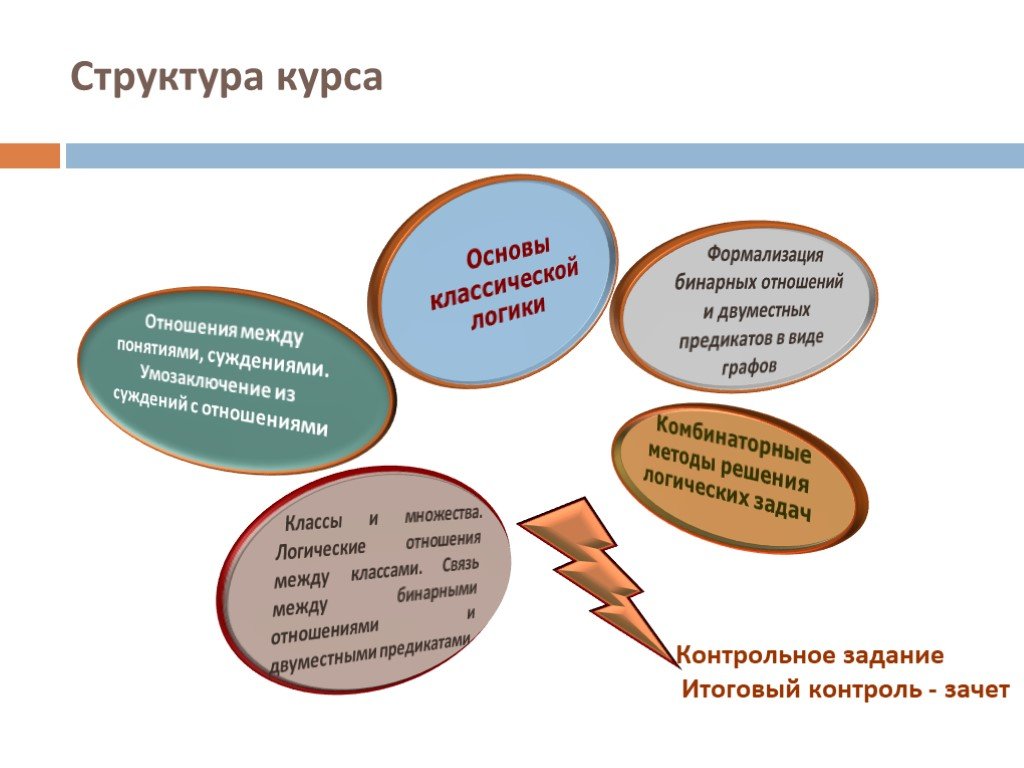
Структура курса

Основы классической логики

Формализация бинарных отношений и двуместных предикатов в виде графов

Классы и множества. Логические отношения между классами. Связь между бинарными отношениями и двуместными предикатами

Отношения между понятиями, суждениями. Умозаключение из суждений с отношениями

Комбинаторные методы решения логических задач

Контрольное задание Итоговый контроль - зачет

Литература

Учебник логики. Со сборником задач: учебник/ А. Д. Гетманова. М.: КНОРУС, 2011. Логика: учебник/ С.С. Гусев, Э.Ф. Караваев, Г.В. Карпов [и др.]; под. ред. А. И. Мигунова, И.Б. Микиртумова, Б. И. Федорова. М.: Проспект, 2010. Логика: учебно-методическое пособие/ В. Н. Ксенофонтов. М.: Изд-во РАГС, 2010.

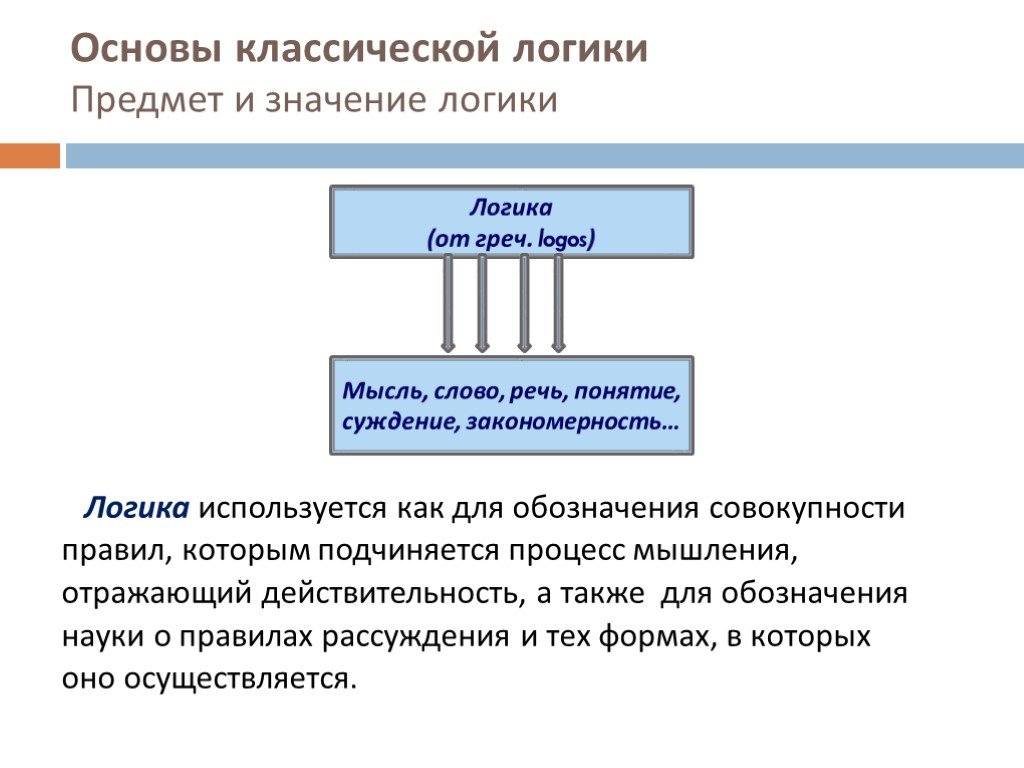
Основы классической логики Предмет и значение логики

Логика используется как для обозначения совокупности правил, которым подчиняется процесс мышления, отражающий действительность, а также для обозначения науки о правилах рассуждения и тех формах, в которых оно осуществляется.

Логика (от греч. logos)

Мысль, слово, речь, понятие, суждение, закономерность…

Основная цель изучения логики – выяснение условий достижения истинных знаний, изучение внутренней структуры мыслительного процесса, выработка специфического логического аппарата. Практическое значение логики - повышение культуры мышления, которое становится более аргументируемым, эффективным и продуктивным. Как следствие – получение из одних истинных суждений другие и опровержение ложных .

Основы классической логики Этапы развития

Деление на этапы с точки зрения применяемых в логике средств и методов исследования: Первый этап - связан с работами древнегреческого ученого и философа Аристотеля (традиционная). Он систематизировал изложение логики. Включает разделы: понятие, суждение, умозаключение, законы логики, доказательство и опровержение, гипотеза. Аристотель видел в логике орудие (метод) исследования.

Второй этап - появление математической (символической) логики. Основоположник - немецкий философ Г.Ф. Лейбниц (1646-1716). Начиная с Лейбница в логике в качестве метода исследования используется метод формализации. Он пытался построить универсальный язык, с помощью которого споры между людьми разрешались вычислениями. В ХIХ веке математическая логика получила развитие в работах Д. Буля, Э. Шредера, П.С. Порецкого, Г. Фреге и других.

Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного (логического ) вывода. Разрабатывает применение математических методов к анализу форм и законов доказательного рассуждения.

Основы классической логики Виды логик (классическая и неклассическая)

Классическая логика - одно из направлений математической логики, которое вслед за традиционной логикой каждому высказыванию приписывает лишь одно из двух истинностных значений: истину или ложь.

Неклассическая логика - направление математической логики, которое исключает применение двузначной логики в рассуждениях о бесконечных множествах. Основоположник - голландский математик Луитцен Ян Эгбертус Брауэр (1881-1966).

Трехзначная логика-высказывание может быть «истинно», «ложно», «нейтрально», а многозначная - истинностные значения: «вероятность»,«возможность», «невероятность», «невозможность» и т.п.). Многозначные логики находят применение при решении парадоксов классической математической логики, в квантовой механике, в теории релейно-контактных схем.

Основы классической логики Понятие как форма мышления

Понятие – форма мышления, в которой отражаются существенные признаки предмета или класса однородных предметов. Признаки – это мысли о свойствах и отношениях предметов. Признаки бывают существенные (необходимые признаки, без которых предмет не может существовать в своей качественной определенности) и несущественные (второстепенные по важности признаки, теряя которые предмет остается самим собой).

Основы классической логики Понятие и представление

Любые понятия так или иначе связаны с ощущениями, представлениями, которые возникают в результате воздействия объектов реальной действительности на органы чувств человека. Представление служит необходимой предпосылкой от чувственного познания к абстрактному мышлению в логической форме понятий. Представление связано с конкретным человеком с его знанием и опытом, оно индивидуализировано. Понятие - не зависит от данного лица и является обобщенным и опосредованным продуктом преобразования чувственного материала в голове человека.

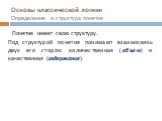
Основы классической логики Определение и структура понятия

Понятие имеет свою структуру. Под структурой понятия понимают взаимосвязь двух его сторон: количественная (объем) и качественная (содержание).

Основы классической логики Содержание и объем понятия

Объем понятия - это совокупность предметов (класс), объединенных в этом понятии. Объем понятия может быть конечным (планеты Солнечной системы, студенты РАНХ и ГС) и бесконечным (растение, товар). Содержание понятия – множество признаков предмета, объединенных в понятии. Например, содержанием понятия «ромб» является совокупность двух существенных признаков: «быть параллелограммом», «иметь равные стороны».

Основы классической логики Понятие и термин

Если понятие – это форма мысли, то ее можно выразить словами или словосочетаниями, отражающими предмет. Не всякое слово выражает понятие (междометия: «ой», «ай»; местоимения: «я», «он»). Понятие и слово не всегда однозначно соответствуют друг другу. Это связано с наличием в одном языке слов-синонимов и слов-омонимов. Их наличие часто ведет к неясности в рассуждениях и аргументации. Поэтому пользуются словами-терминами, точно выражающими содержание научных понятий.

Терминами (от лат. terminus - граница, предел) называют слова и словосочетания, которые предназначаются для максимально строгого и точного выражения тех или иных понятий.

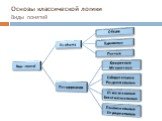
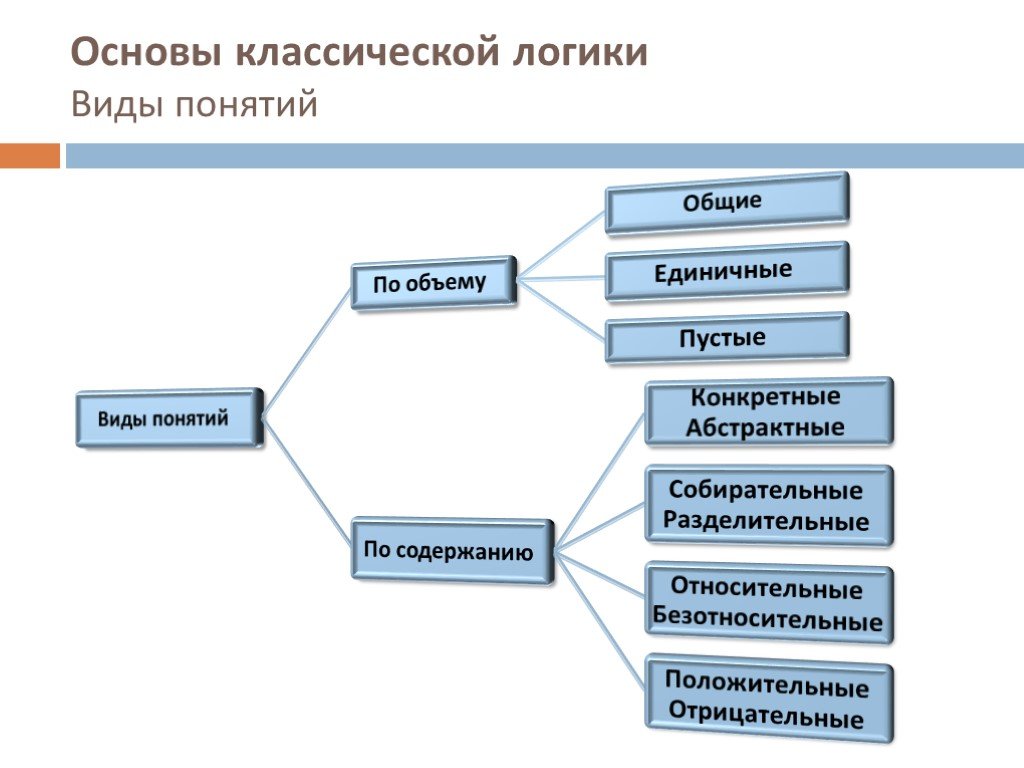
Основы классической логики Виды понятий

Основы классической логики Виды понятий “По объему”.

Единичными называются понятия, которые соответствуют классам (множествам), состоящим из одного элемента. Например, «столица России», «ООН». Общими называются понятия, которые соответствуют классам (множествам), состоящим из двух и более элементов. Например, «человек», «звезда». Пустыми называются понятия объемы которых представляют собой классы реально не существующих предметов и существование которых не возможно. Например, «Баба Яга», «вечный двигатель».

Основы классической логики Виды понятий “По содержанию”.

Конкретными называются понятия, в которых отражены одноэлементные или многоэлементные классы предметов. Например, «дом», «поэма Маяковского «Хорошо!». Абстрактными называются понятия, в которых мыслится не сам предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета. Например, «смелость», «белизна».

Относительные – это понятия, в которых мыслятся предметы, существование одного из которых предполагает существования другого. Например, «дети» - «родители», «студент»- «преподаватель». Безотносительные это понятия, в которых мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета. Например, «завод», «деревня», «доменная печь».

Собирательным называются понятия, в которых класс однородных предметов мыслится как единое целое. Например, «толпа», «лес», «полк». Содержание разделительного понятия можно отнести к каждому предмету данного класса, мыслимого в понятии. Например, «дом», «театр», «студент».

Положительные понятия характеризуют в предмете наличие того или иного качества или свойства. Например, «грамотный человек», «принципиальность», «ненастье», «беспечность». Нельзя сказать «настье», «печность». Отрицательными называются понятия, в содержании которых указывается на отсутствии у предмета определенных свойств. Например, «некрашеный дом», «бескорыстная помощь».

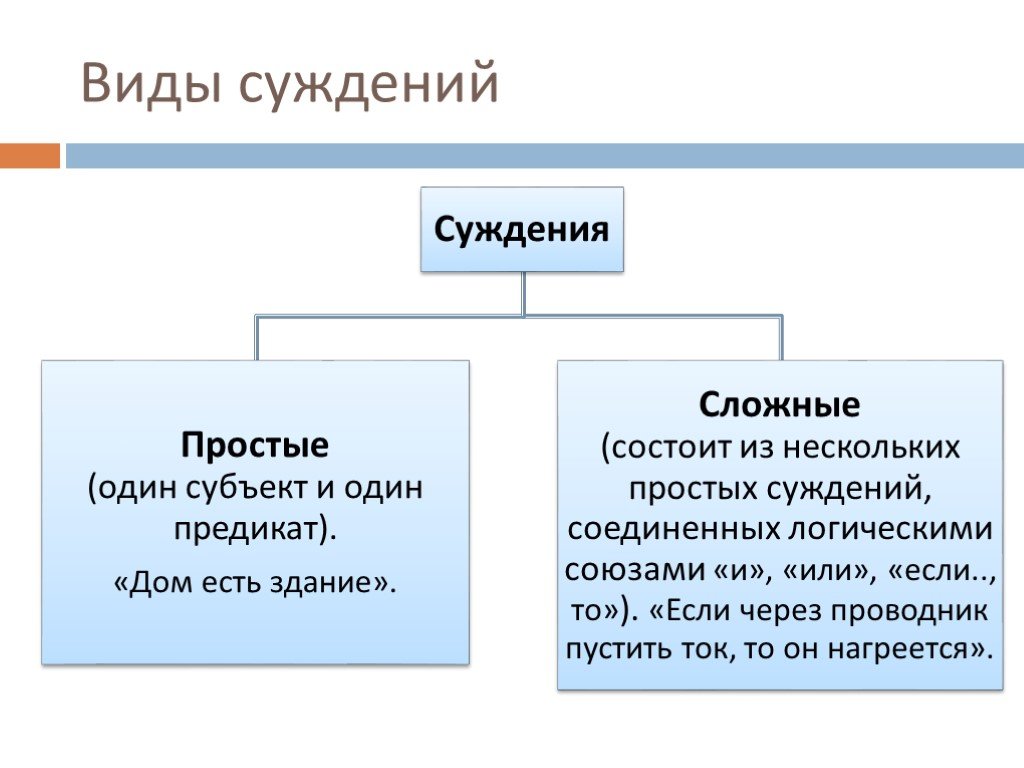
Суждения…

Суждение

Суждение - это форма мышления, в которой утверждается или отрицается что-либо относительно предметов и явлений, их свойств, связей или отношений и которая обладает свойством выражать либо истину либо ложь. Например, «Земля - это планета», «Эгейское море старше черного моря».

Всякое суждение выражается в предложении, но не всякое предложение выражает суждение. Вопросительные предложения не являются суждениями, т.к. они не поддаются логическому анализу. Многие побудительные предложения не выражают суждения («Берегите лес!», «Войдите!»). Но побуждения к определенным целенаправленным действиям приобретают характер суждения («Ни шагу назад!», «В атаку!»).

Суждение и предложение различаются по своему составу. Суждение состоит из 4-х структурных элементов: субъект суждения - это понятие о предмете мысли т.е. то о чем говорится в данном суждении (обозначается «S»); предикат суждения выражает значение о признаке предмета мысли, т.е. что говорится о субъекте суждения (обозначается «Р»);

связка выражает отношения, установившиеся в суждении между субъектом и предикатом, и характеризует принадлежность предмету мысли того или иного свойства, отраженного в предикате (обозначается «-», «есть», «не является», «имеется»). квантор (кванторное слово) указывает, относится ли суждение ко всему или к части объема понятия, выражающего субъект («все», «некоторые», «многие», «ни один») . Квантор может в суждении отсутствовать.

Состав суждения можно выразить общей формулой: S есть P или S не есть P . Например. В суждении «Некоторые люди являются долгожителями» кванторное слово – «некоторые», субъект – «люди», предикат – «долгожителями», связка – «являются». Структура суждения выражается формулой: «Некоторые S есть P».

Виды суждений

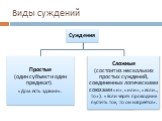
Классификация суждений по качеству и количеству

Виды простых суждений, которые классифицируются по следующим основаниям. 1. По объему субъекта (по количеству). Единичные - суждения, включающие утверждение или отрицание об одном предмете. Формула такого суждения: «Это S есть (не есть) P». Например, суждение «Везувий - действующий вулкан» - единичное суждение, так как объем субъекта включает конкретное место.

Частные - суждения, в которых что-либо утверждается или отрицается о части предметов некоторого класса. Эта часть может быть неопределенной и определенной. В неопределенных суждениях логическая схема такова: «Некоторые S есть Р». Слово «некоторые» придает им неопределенность. Например: «Некоторые цветы-розы». Определенное частное суждение содержит знание и о той, и о другой части субъекта суждения. Имеет логическую схему: «Только некоторые S есть Р». Например: «Только некоторые ягоды съедобные».

Объединенная классификация суждений по качеству и количеству

Общие - суждения, в которых что-либо утверждается или отрицается в каждом предмете данного класса. Логическая схема имеет вид: «Все S есть Р» или «Ни одно S не есть Р». Например: «Все здравомыслящие люди хотят долгой, счастливой и полезной жизни» - является общим суждением, так как объем субъекта включает весь класс отображаемых предметов.

2. По качеству связки суждения могут быть утвердительные или отрицательные. Утвердительные – это суждения, выражающие принадлежность предмету некоторого признака: например, «Научная организация труда повышает эффективность деятельности инженера».

Отрицательные – это суждения, выражающие отсутствие у предмета некоторого признака: например, «Ни один дельфин не является рыбой». Следует различать отрицательное суждение и негативную форму выражения утвердительного суждения: например, «Захватническая война не имеет законного основания» и «Захватническая война – незаконна». Такие суждения не всегда идентичны. Представленные утвердительные и отрицательные суждения называются категорическими суждениями.

3. По содержанию предиката суждения делятся на суждения свойства(атрибутивные), суждения отношения (релятивные) и суждения существования(экзистенциальные). Суждения свойства отражают принадлежность или непринадлежность предмету мыслимого или иного свойства, состояния. Логическая схема: «S есть Р» или «S не есть Р». Например, «Всякий терьер - собака».

Суждения отношения выражают различные связи между предметами мысли по месту, времени, величине и прочее: например, суждение «Эверест выше Монблана» - определяется отношением (через сравнение) одной горы с другой. Формула: aRb или R(a,b) , где a и b – имена предметов, R- имя отношения. Суждения существования призваны решать вопрос о наличии предмета нашей мысли- любого явления природы, общества или духовной жизни. Например: «Одним из объектов исследования социологии является общественное мнение».

Любое суждение имеет и количественную, и качественную характеристики. Поэтому в логике применяется объединенная классификация суждений по количеству и качеству. В результате получаем четыре вида суждений : общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные.

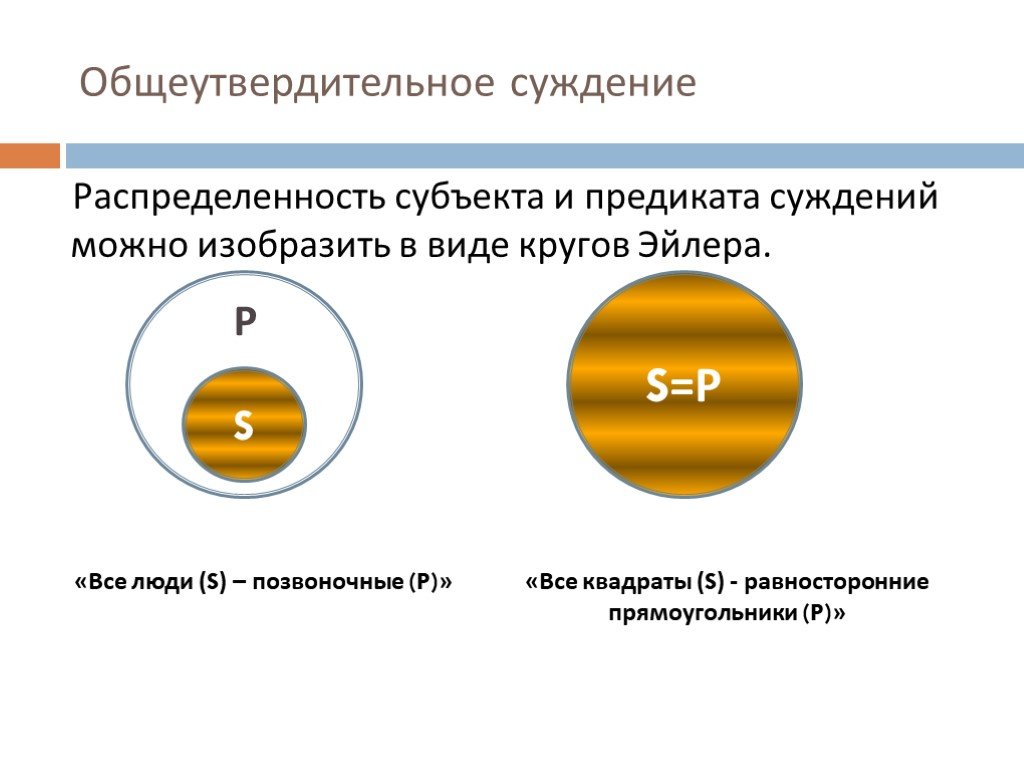
Общеутвердительное суждение

Общеутвердительное суждение - общее по объему и утвердительное по качеству связки. Его структура: «Все S есть Р». Например, «Все люди - позвоночные» или «Все квадраты - равносторонние прямоугольники». В первом суждении объем предиката (P-позвоночные) больше объема субъекта (S-люди) и является его подчиняющим понятием. Во втором - объемные отношения субъекта и предиката равны.

Распределенность субъекта и предиката суждений можно изобразить в виде кругов Эйлера.

З S Р S=Р

«Все люди (S) – позвоночные (P)»

«Все квадраты (S) - равносторонние прямоугольники (P)»

Общеотрицательное суждение

Общеотрицательное суждение - общее по объему субъекта и отрицательное по качеству связки. Его структура: «Ни одно S не есть Р». Например, «Ни один гепард не является травоядным животным». Для всех общеотрицательных суждений характерна полная несовместимость субъекта (S-гепард) и предиката (Р-травоядное), т.е. их объемы полностью исключают друг друга.

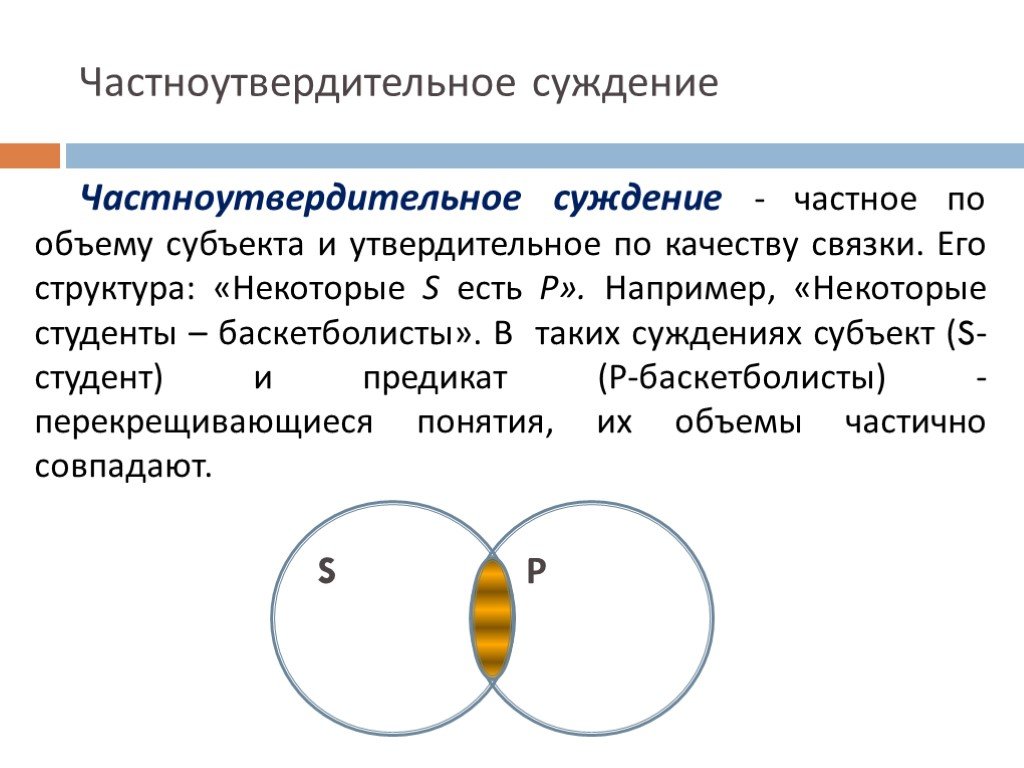
Частноутвердительное суждение

Частноутвердительное суждение - частное по объему субъекта и утвердительное по качеству связки. Его структура: «Некоторые S есть Р». Например, «Некоторые студенты – баскетболисты». В таких суждениях субъект (S-студент) и предикат (Р-баскетболисты) - перекрещивающиеся понятия, их объемы частично совпадают.

В некоторых частноутвердительных суждениях объем субъекта шире объема предиката. Например, «Некоторые актеры - ветераны ВОВ». Объем предиката (Р-ветераны) здесь входит в объем субъекта (S-актеры), но объем субъекта только частично совпадает с объемом предиката. Предикат в этом случае подчинен субъекту.

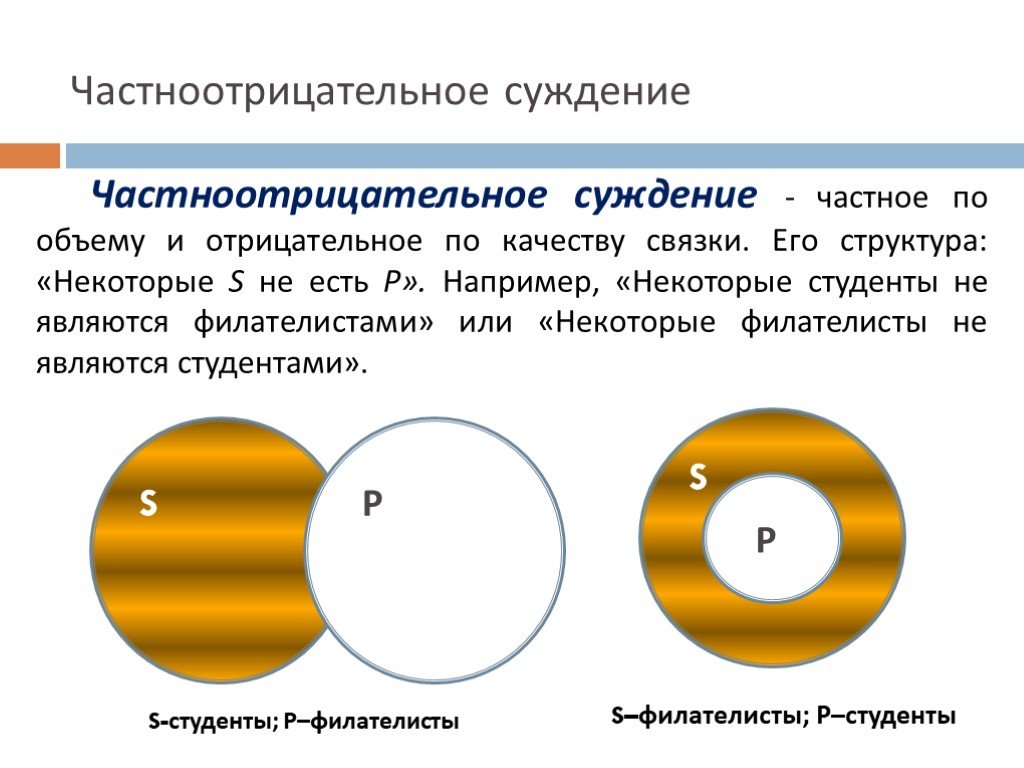
Частноотрицательное суждение

Частноотрицательное суждение - частное по объему и отрицательное по качеству связки. Его структура: «Некоторые S не есть Р». Например, «Некоторые студенты не являются филателистами» или «Некоторые филателисты не являются студентами».

S-студенты; Р–филателисты

S–филателисты; Р–студенты

Комплексный анализ простого категорического суждения

Анализ объема понятий - терминов суждения связан в дальнейшем с выяснением их распределенности. Распределенным термин считается тогда, когда он взят в полном объеме. Если термин взят в части объема, он считается нераспределенным. Исследование распределенности терминов суждения - это не формальная логическая операция, а подтверждение правильной связи данных субъекта и предиката в суждении, т.е. ее соответствия объективному отношению самих предметов.

Правила распределенности терминов: В общеутвердительных суждениях субъект распределен, а предикат нераспределен. Распределенными оба термина будут в случае их равнозначности. В общеотрицательных суждениях оба термина всегда распределены, они полностью исключают друг друга, являются несовместимыми понятиями.

В частноутвердительных суждениях оба термина не распределены, если они выражаются перекрещивающимися понятиями. Если предикат подчинен субъекту, тогда предикат будет распределен. В частноотрицательных суждениях субъект нераспределен, а предикат всегда распределен. Таким образом, субъект распределен в общих суждениях и не распределен в частных суждениях; предикат распределен в отрицательных суждениях и нераспределен в утвердительных суждениях. Исключение составляют общеутвердительные и частноутвердительные суждения, у которых предикат распределен.

Комплексный анализ предполагает, что: определена его логическая структура (форма); показано на кругах Эйлера соотношение терминов (объемов субъекта и предиката) в составе суждения; указана распределенность терминов в составе суждения, на основании чего оно отнесено к одному из четырех видов объединенной классификации.

Виды суждений, не рассматриваемых в классической логике

Т.о., раскрыв сущность, содержание и специфику суждений можно прийти к выводу о том, что мысли человека всегда формируются в суждениях, которые могут быть либо истинными, либо ложными. Суждение дает уже готовую мысль, фиксирует ее, но не развивает. Для развития мысли, получения нового знания о мире, требуется более сложная форма мышления; она называется умозаключением.

Спасибо за внимание…