Презентация "Логика" (7 класс) по обществознанию – проект, доклад
Презентацию на тему "Логика" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Обществознание. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
Логика
Используемые источники:. Уневерсальные тесты профессора Айзенка. –СПб.: « Стелла» 2009. 2.Волина В.В. Учимся играя. – М.: Новая школа, 1994. 3.Максимова ...Логика – наука о формах и способах мышления
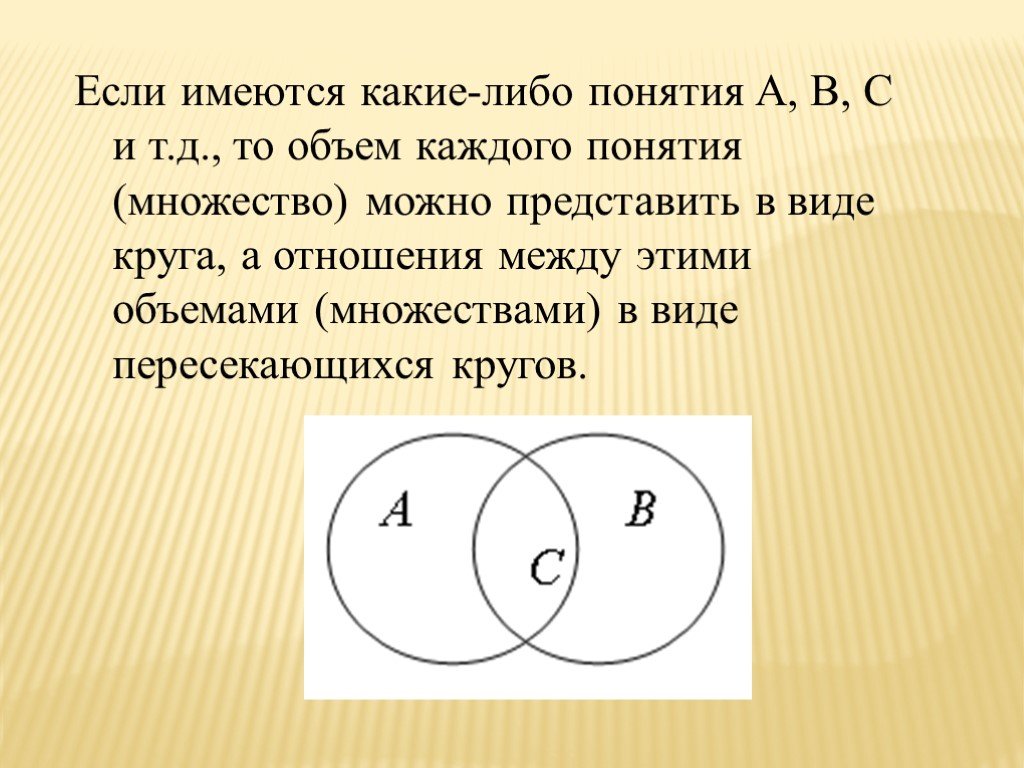
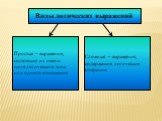
Понятие –это форма мышления, фиксирующая основные, существенные признаки объекта. Содержание Объем. Высказывание -. это форма мышления, в которой ...Логика
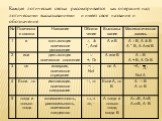
Найди недостающую фигуру и объясни свой выбор. Нажми на звонок под выбранной тобой фигурой. . . . . . . . . . Используемые источники:. Уневерсальные ...Введение в обществознание
Ожидаемые учебные результаты:. Человечки-подсказки. Человечек-вопрос Человечек-галочка Человечек-спортсмен Человечек-Архимед Человечек-память. «У ...Введение в предмет обществознание
Цель урока. Создать условия для определения значимости изучения предмета обществознание, через формирование суждений о возможности применения знаний ...Наука и образование
Что такое наука? наука Система знаний. Функции современной науки.эпоха функции. Этика науки.
система этических норм. Образование.
переустройство ...
Наука и образование
План урока. 1. Наука в современном обществе 2. Этика науки 3. Потребности современного образования. 1. Наука в современном обществе. Наука – творческая ...Наука и образование в 1-й половине XIX века
Общеобразовательные учреждения. Приходские школы Уездные училища Гимназии. Предметы: 1) география; 2) Закон Божий; 3) математика; 4) арифметика; 5)история; ...Наука и образование
24.12.2017. Антоненкова Анжелика Викторовна МОУ Будинская ООШ. 1. Академия наук. 2. М.В. Ломоносов. 3. Естественные науки. 4. Гуманитарные науки. ...Наука и образование
Как защититься от несправедливости: (памятка). 1.Знай, право должно защищать любого человека, помогать ему в трудных ситуациях; 2. Нужно позаботиться ...Задачи профильного обучения по курсу обществознание
1.В семейно-бытовой сфере. Вести себя сообразно нравственным и правовым нормам, активно участвовать в делах семьи и решении ее проблем. 2.В сфере ...Поведение и поступок обществознание
ПОВЕДЕНИЕ. Поведением в психологии называют любые внешние проявления активности. Активность человека имеет внешнюю и внутреннюю стороны. Внешнюю же, ...Что такое общество
Общество. Жители какой-нибудь страны, которых связывают друг с другом их настоящее, их история, их культура. Все люди, живущие на Земле. Так можно ...Социология как наука
Объект и предмет социологии. Специфика предмета социологии. Место социологии в системе научного знания. Структура социологии. Функции социологии. ...Человек и общество
1.Природное и общественное в человеке. (Человек как результат биологической и социокультурной эволюции.) 2. Мировоззрение, его виды и формы 3. Виды ...Российское образование (по результатам международного исследования pisa-2012)
Programme for International Student Assessment. Основная цель: оценка способности 15-летних учащихся использовать приобретенные в школе знания и опыт ...Современное общество
Цели и задачи урока. На занятии мы будем объяснять понятия «мировое сообщество», «научно-техническая революция», «мегаполис», «социальное неравенство», ...Право на образование
План урока. Личностная и социальная значимость образования. Содержание права на образование. Тенденции развития образования в современном мире. Структура ...Природа и общество
Примитивные формы объединения. Развитие человека. Изменения в жизни человека. Человек --> труд (речь, мышление, обычаи, традиции) --> группы людей--> ...Гражданское общество и правовое государство
Домашнее задание. §6 читать; Ответь на вопросы и задания после §6; Решить проблему, выполнить практикум; Новые слова выучить; Рабочая тетрадь, задания ...Конспекты
Логика в современном мире
Бзыкова Белла Тамбиева. учитель истории и обществознанияМОУ СОШ с. .Хумалаг. . . «Логика в современном мире». Программа курса. ...Логика
Областная специализированная школа-интернат № 4 для одаренных детей «Болашак». Конспект урока обществознания на тему. «Логика». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 октября 2018
Категория:Обществознание
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию