Слайд 1Средние величины и показатели вариации
Слайд 2Понятие средней величины
Средняя величина
Обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в условиях конкретного время и места
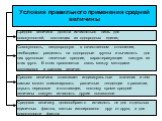
Слайд 3Условия правильного применения средней величины
Средняя величина должна исчисляться лишь для совокупностей, состоящих из однородных единиц
Совокупность, неоднородную в качественном отношении, необходимо разделять на однородные группы и вычислять для них групповые типичные средние, характеризующие каждую из этих групп. В этом проявляется связь между методами группировок и средних величин
Средняя величина сглаживает индивидуальные значения и тем самым может элиминировать различные тенденции в развитии, скрыть передовое и отстающее, поэтому кроме средней величины следует исчислять другие показатели
Среднюю величину целесообразно исчислять не для отдельных единичных фактов, взятых изолированно друг от друга, а для совокупности фактов
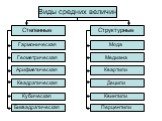
Слайд 4Виды средних величин
Степенные Структурные Гармоническая Геометрическая Арифметическая Квадратическая Кубическая Биквадратическая Мода Медиана Квартили Децили Квинтили Перцентили
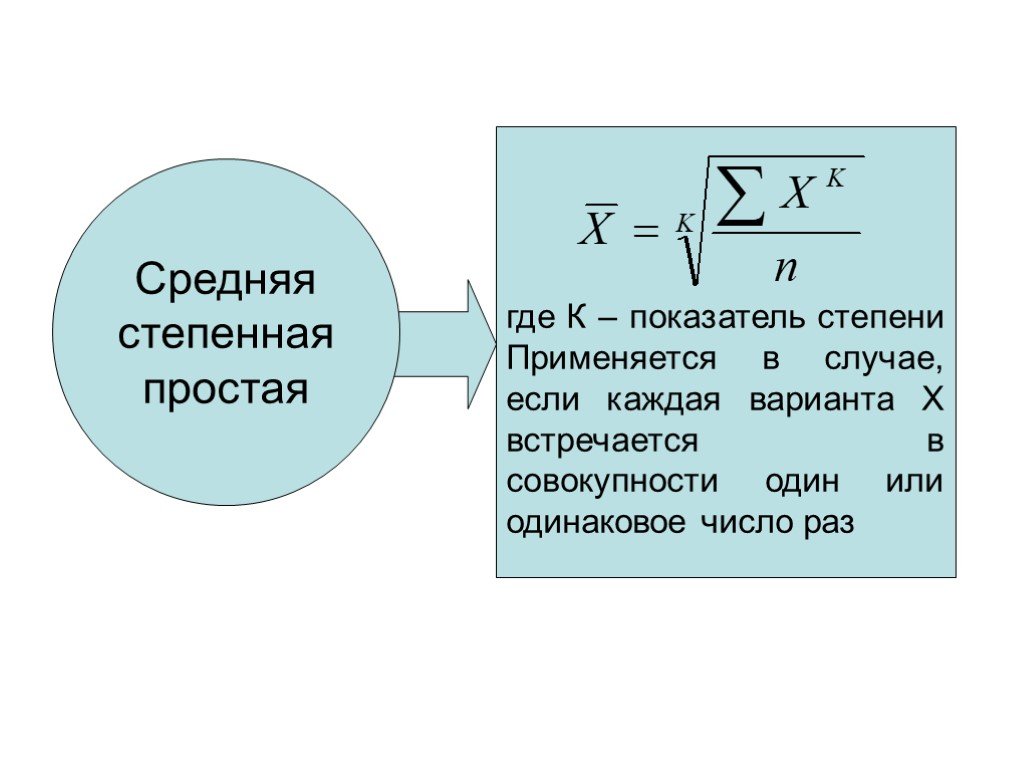
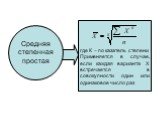
Слайд 6Средняя степенная простая
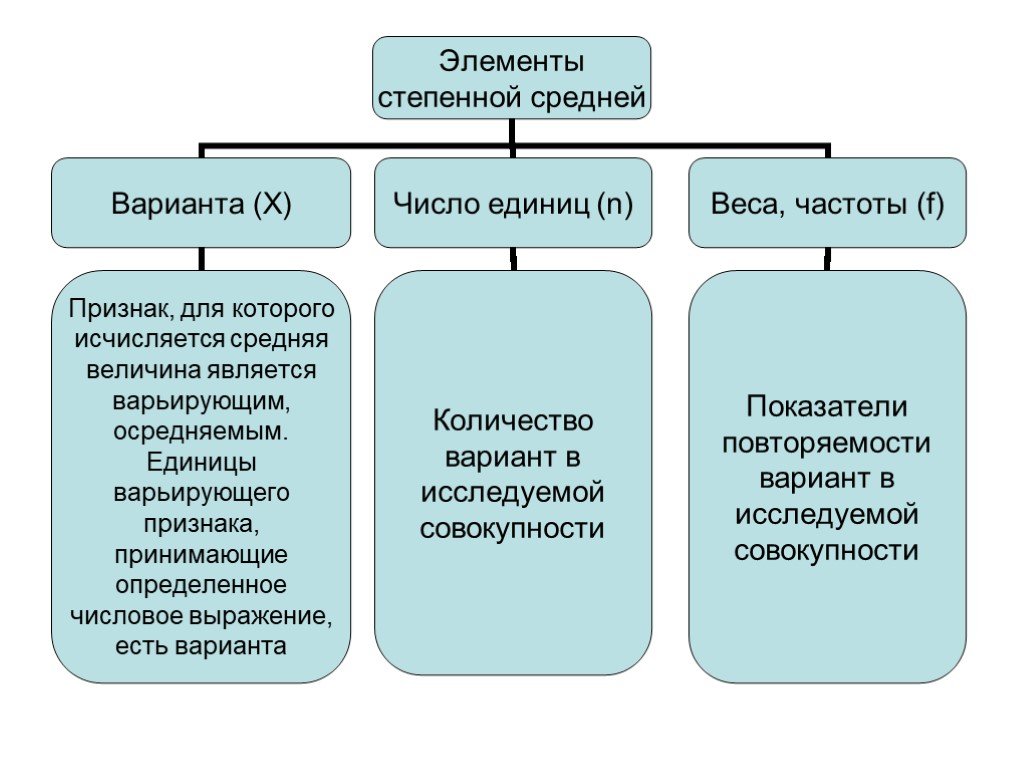
где К – показатель степени Применяется в случае, если каждая варианта Х встречается в совокупности один или одинаковое число раз
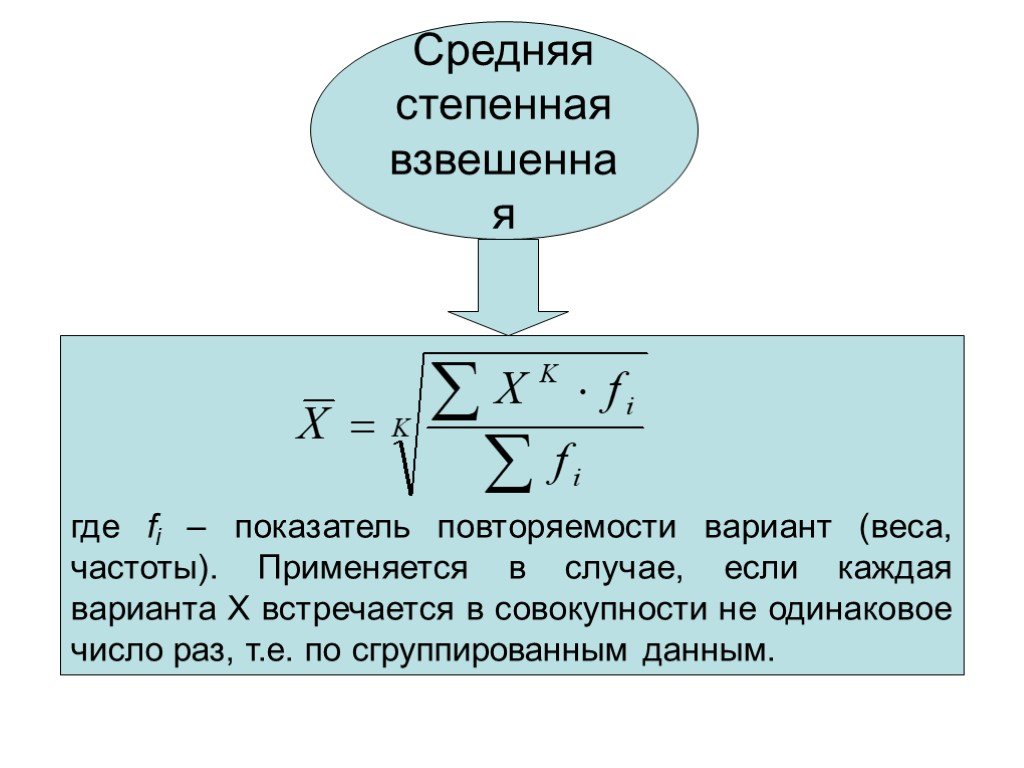
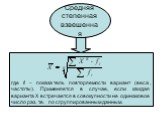
Слайд 7Средняя степенная взвешенная
где fi – показатель повторяемости вариант (веса, частоты). Применяется в случае, если каждая варианта Х встречается в совокупности не одинаковое число раз, т.е. по сгруппированным данным.
Слайд 8К=-1; или где ω=xi*fi Средняя гармоническая применяется в случае, если известны варьирующие обратные значения признака.
Средняя гармоническая
Слайд 9К=0; или Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения
Средняя геометрическая
Слайд 10К=1; или Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака отдельных ее единиц.
Средняя арифметическая
Слайд 11К=2; или
Средняя квадратическая
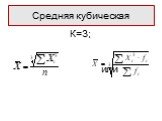
Слайд 12К=3; или
Средняя кубическая
Слайд 13К=4; или
Средняя биквадратическая
Слайд 14Для одной и той же совокупности существуют строго определенные соотношения между разными видами средних. Эти соотношения называют правилом мажорантности средних.
Правило мажорантности средних
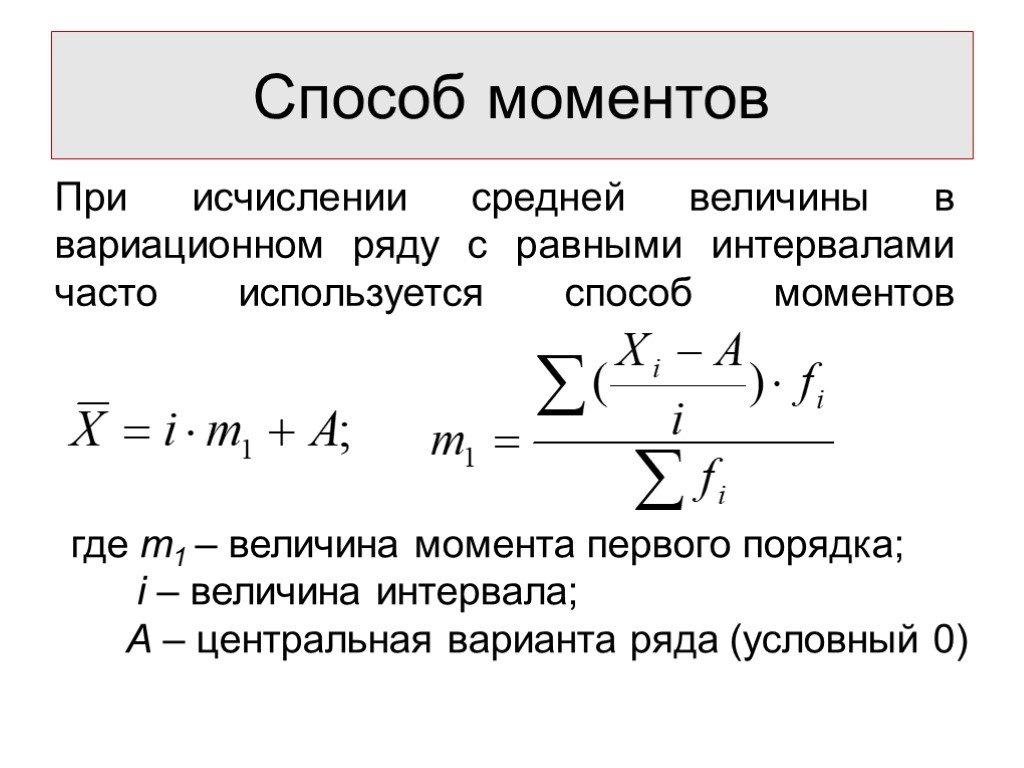
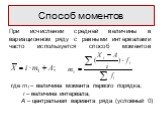
Слайд 15При исчислении средней величины в вариационном ряду с равными интервалами часто используется способ моментов
Способ моментов
где m1 – величина момента первого порядка; i – величина интервала; А – центральная варианта ряда (условный 0)
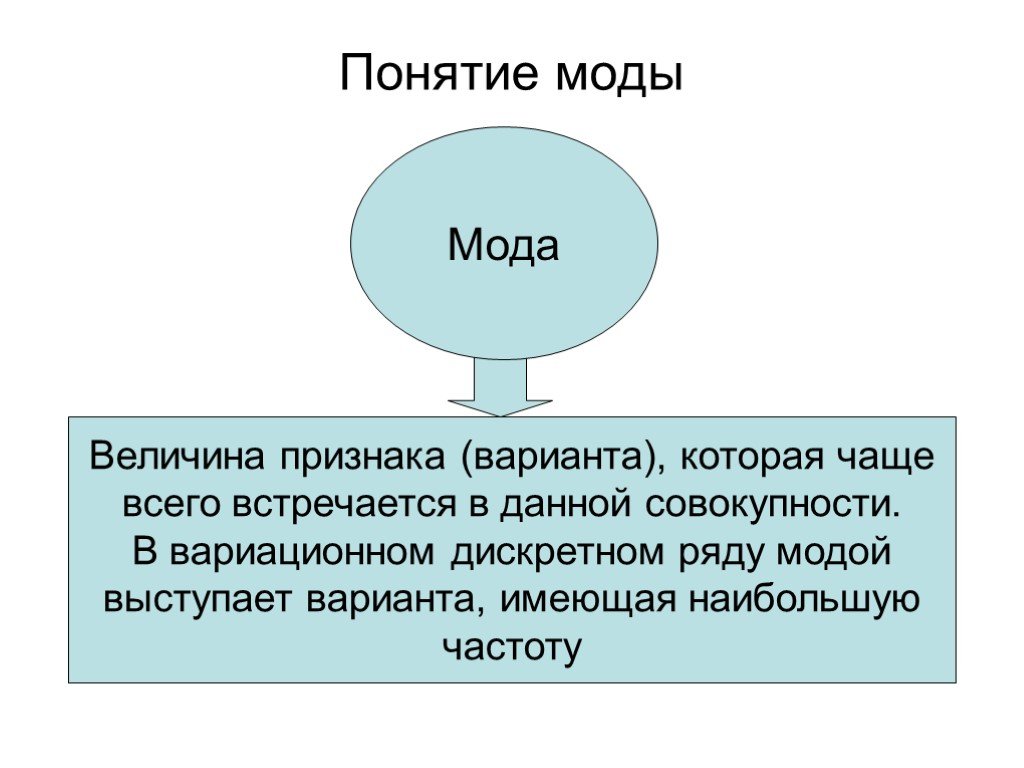
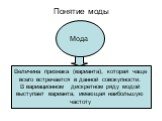
Слайд 16Понятие моды
Величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном дискретном ряду модой выступает варианта, имеющая наибольшую частоту
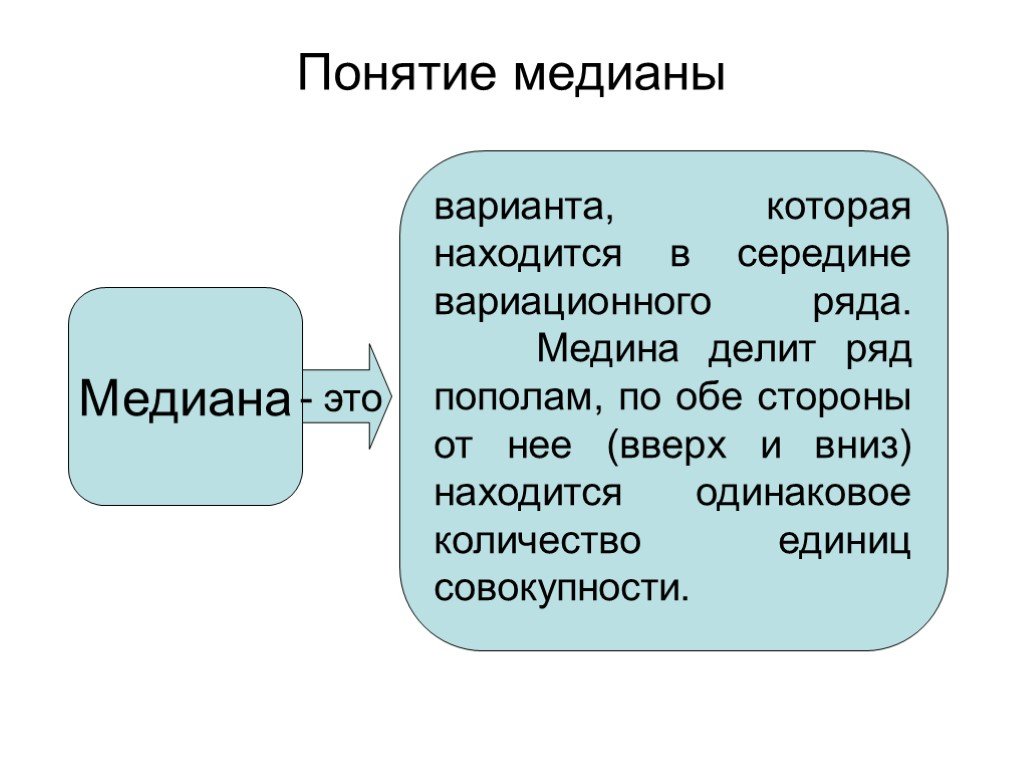
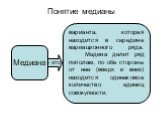
Слайд 17Понятие медианы
варианта, которая находится в середине вариационного ряда. Медина делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.
- это
Слайд 18В интервальных рядах с равными интервалами мода вычисляется по формуле где X0 – минимальная граница модального интервала; i – величина модального интервала; fm – частота модального интервала; fm-1 – частота интервала, предшествующего модальному; fm+1 – частота интервала, следующего за модальным; Модальный интервал в интервальном ряду определяется по наибольшей частоте.
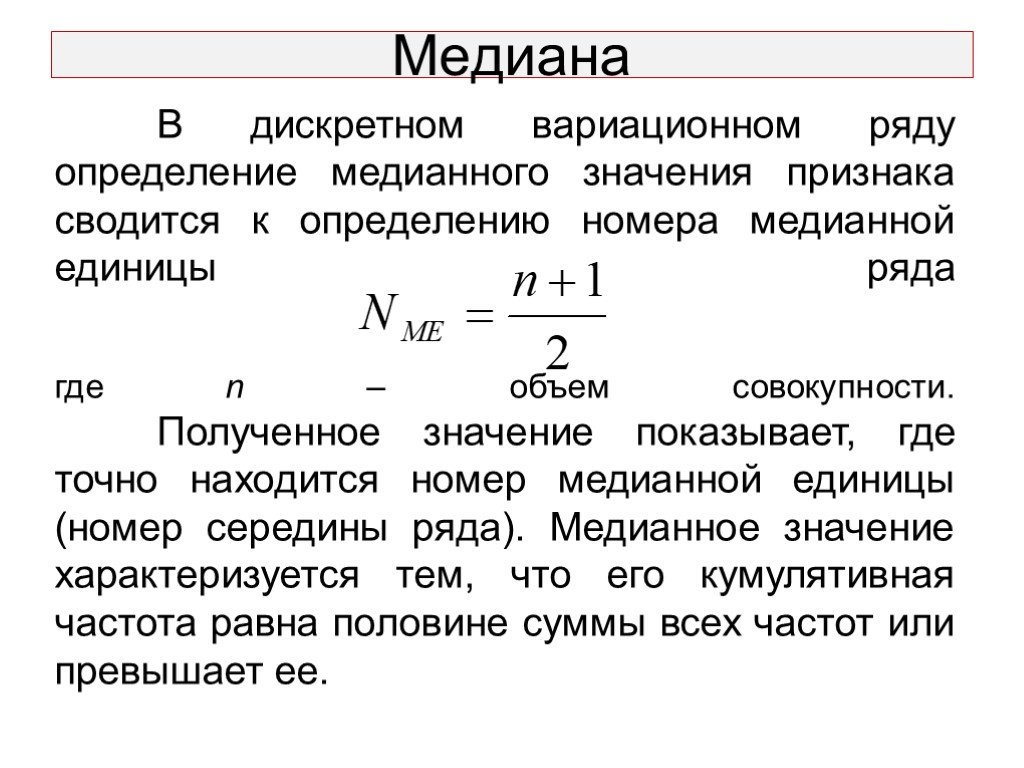
Слайд 19В дискретном вариационном ряду определение медианного значения признака сводится к определению номера медианной единицы ряда где n – объем совокупности. Полученное значение показывает, где точно находится номер медианной единицы (номер середины ряда). Медианное значение характеризуется тем, что его кумулятивная частота равна половине суммы всех частот или превышает ее.
Слайд 20В интервальных рядах с равными интервалами медиана исчисляется по формуле где X0 – начальное значение медианного интервала; i – величина медианного интервала; Σf – сумма частот ряда; Sm-1 – сумма накопленных частот в интервалах, предшествующего медианному; fm – частота медианного интервала. Для определения медианного интервала необходимо рассчитать сумму накопленных частот. Медианный интервал характерен тем, что его кумулятивная частота равна полусумме всех частот ряда или превышает ее.
Слайд 21Значения признака, делящее ранжированную совокупность на четыре равные части. Различают нижний квартиль (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и верхний квартиль (Q3), отсекающий ¼ часть с наибольшими значениями признака. Средний квартиль (Q2) совпадает с медианой (Me). Для расчета квартилей по интервальному вариационному ряду используют формулы
Слайд 22; где XQ1 (XQ3) – нижняя граница интервала, содержащего нижний (верхний) квартиль; i – величина интервала; SQ1-1 (SQ3-1) – накопленная частота интервала, предшествующего интервалу, содержащий нижний (верхний) квартиль ; fQ1(fQ3) – частота интервала, содержащего нижний (верхний) квартиль.
Слайд 23Варианты, делящие ранжированный ряд на 10 равных частей; они вычисляются по той же схеме, что и квартили:
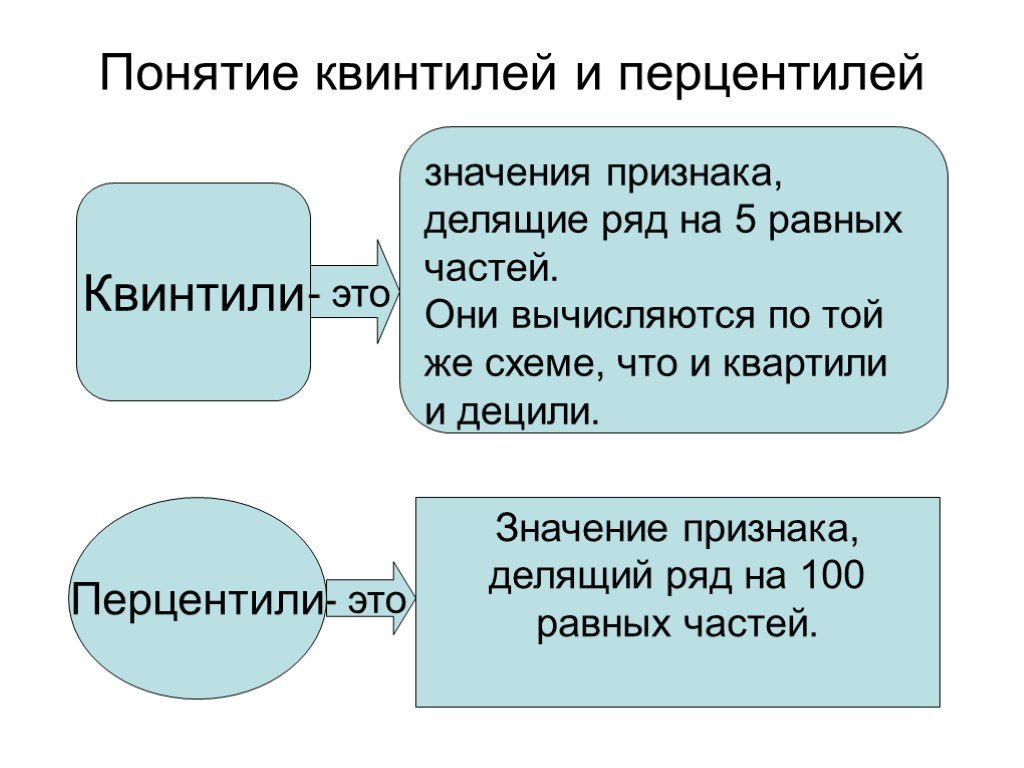
Слайд 24Понятие квинтилей и перцентилей
значения признака, делящие ряд на 5 равных частей. Они вычисляются по той же схеме, что и квартили и децили.
Значение признака, делящий ряд на 100 равных частей.
Слайд 25Понятие вариации Вариация
колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.
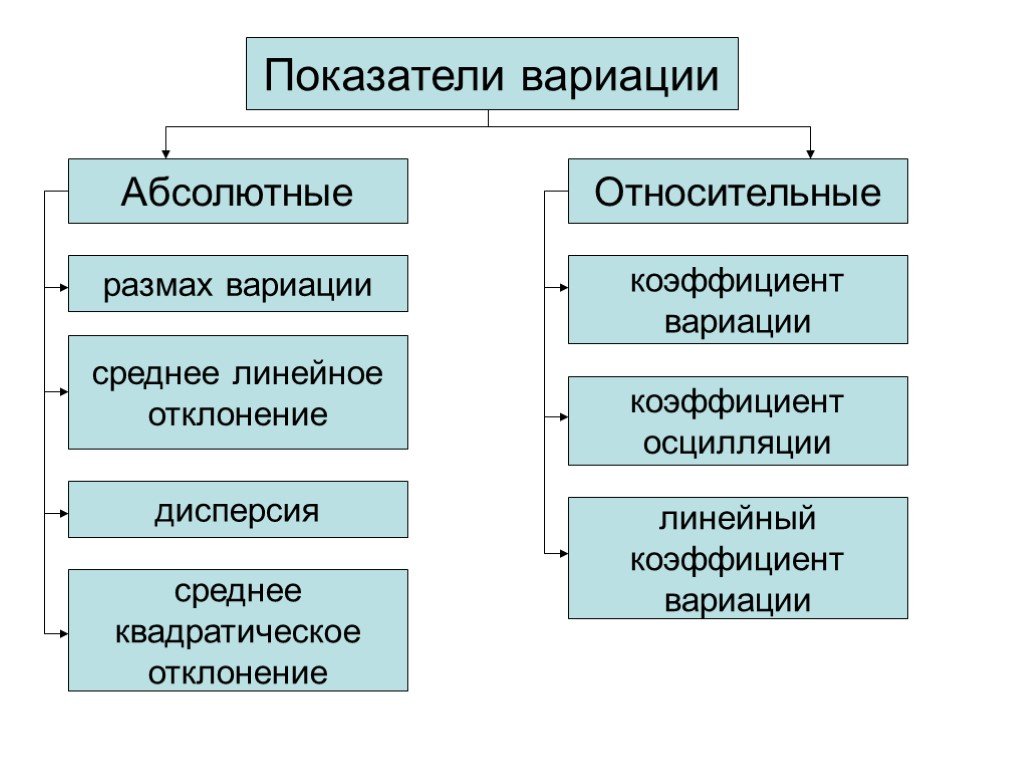
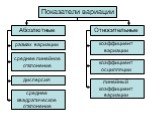
Слайд 26Показатели вариации
Абсолютные Относительные размах вариации
среднее линейное отклонение
дисперсия
среднее квадратическое отклонение
коэффициент вариации
коэффициент осцилляции
линейный коэффициент вариации
Слайд 27Размах вариации
Характеристика границ вариации изучаемого признака. Определяется по формуле R= Xmax –Xmin , где Xmax- максимальное значение варьирующего признака; Xmin- минимальное значение варьирующего признака. Показывает, сколь велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака, основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду.
Слайд 28Дисперсия
Средний квадрат отклонений индивидуальных значений признака от их средних величин. Вычисляется по следующим формулам: 1-й способ: или где Xi – индивидуальное значение варьирующего признака (варианты); - среднее значение варьирующего признака; n – количество разновидностей вариант; fi - показатель повторяемости вариант (частоты, веса).
Слайд 29где – средняя из квадратов индивидуальных значений; – квадрат средней величины признака.
2-ой способ определения дисперсии
Слайд 303-й способ определения дисперсии - метод моментов
где m1 – величина момента первого порядка; i – величина интервала в интервальном ряду; m2 – величина момента второго порядка:
Слайд 31Обобщающая характеристика размеров вариации признака в совокупности определяется по формуле
Среднее квадратическое отклонение
Показывает, на какую величину в среднем значение признака отличается от стандартного значения, и выражается в тех же единицах, что и признак.
Слайд 32Среднее линейное отклонение
Показывает на какую величину отклоняется признак в изучаемой совокупности от средней величины признака: Показатель рассчитывается по модулю.
Слайд 33Коэффициент вариации
Характеристика меры вариации значений признака вокруг средней величины: Чем этот показатель меньше, тем однороднее совокупность, а средняя величина признака типична для данной совокупности. Чем коэффициент вариации больше, тем неоднороднее совокупность.
Слайд 34Линейный коэффициент вариации и коэффициент осцилляции
Линейный коэффициент вариации: Коэффициент осцилляции:
Слайд 35Математические свойства дисперсии
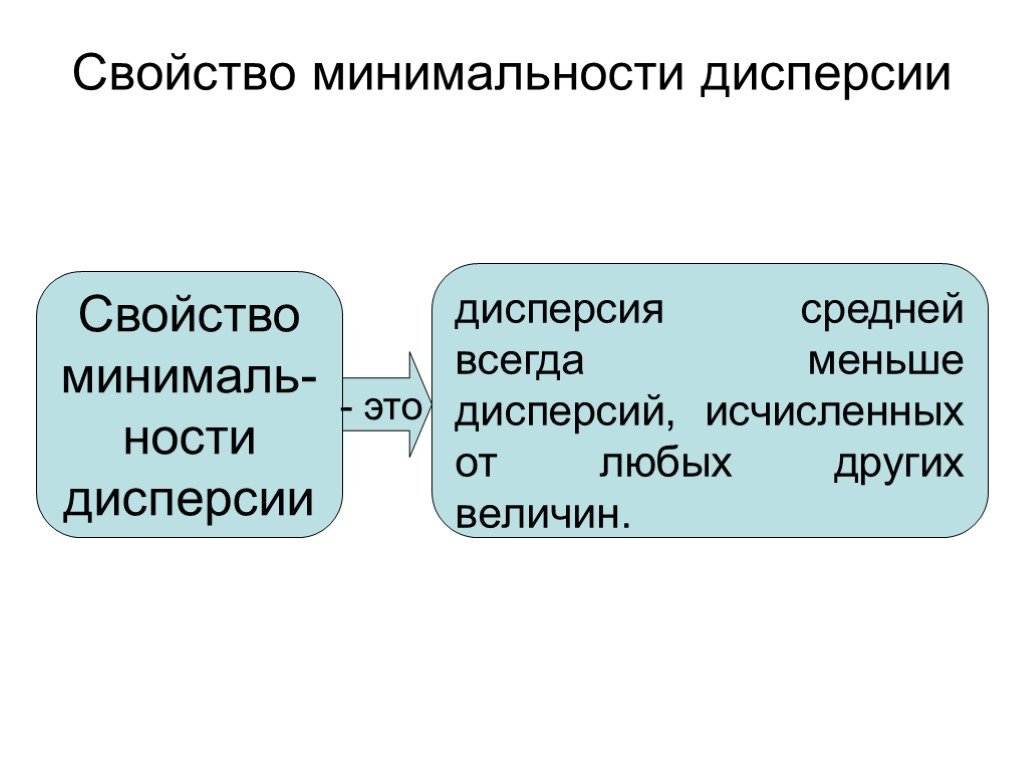
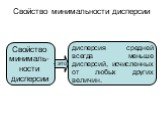
Слайд 36Свойство минимальности дисперсии
Свойство минималь-ности дисперсии
дисперсия средней всегда меньше дисперсий, исчисленных от любых других величин.
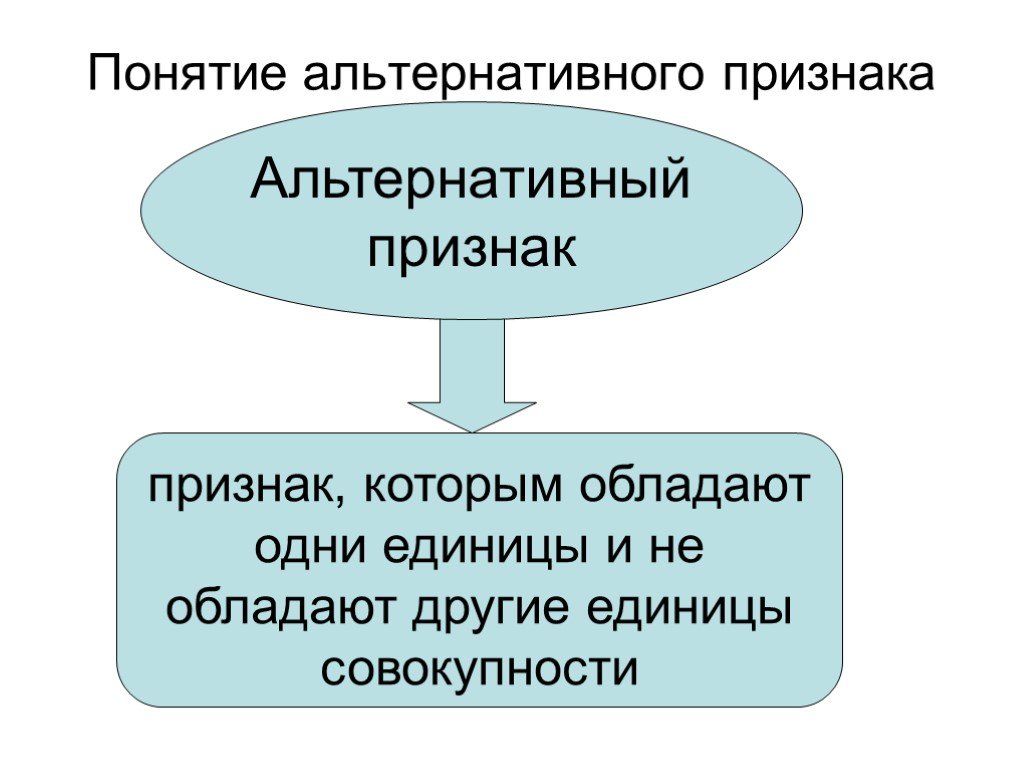
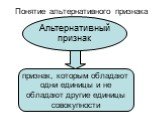
Слайд 37Понятие альтернативного признака
признак, которым обладают одни единицы и не обладают другие единицы совокупности
Альтернативный признак
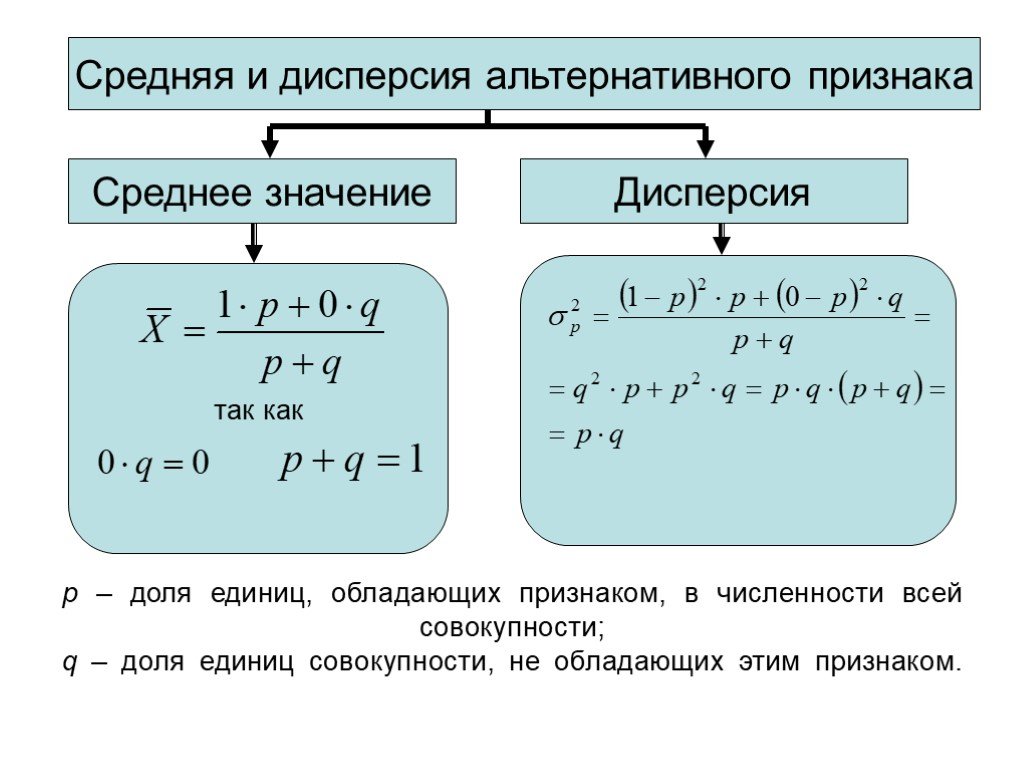
Слайд 38так как
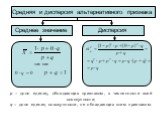
Средняя и дисперсия альтернативного признака
Среднее значение
p – доля единиц, обладающих признаком, в численности всей совокупности; q – доля единиц совокупности, не обладающих этим признаком.
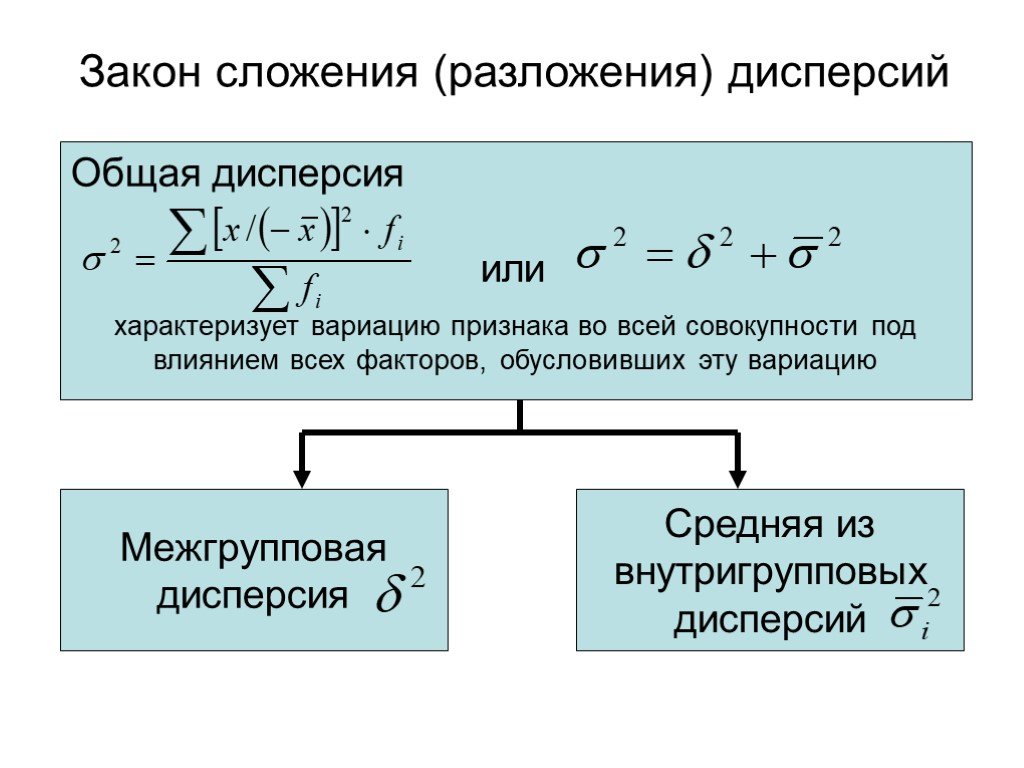
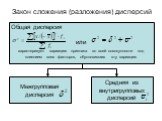
Слайд 39Общая дисперсия или характеризует вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию
Межгрупповая дисперсия
Средняя из внутригрупповых дисперсий
Закон сложения (разложения) дисперсий
Слайд 40Характеризует вариацию изучаемого признака под влиянием признака-фактора, положенного в основание группировки:
где - общая средняя; - средняя i - группы; fi – частота i - ой группы.
Слайд 41Отражает случайную вариацию, обусловленную неучтенными факторами и не зависящую от признака-фактора, положенного в снование группировки
где - внутригрупповая дисперсия i – ой группы
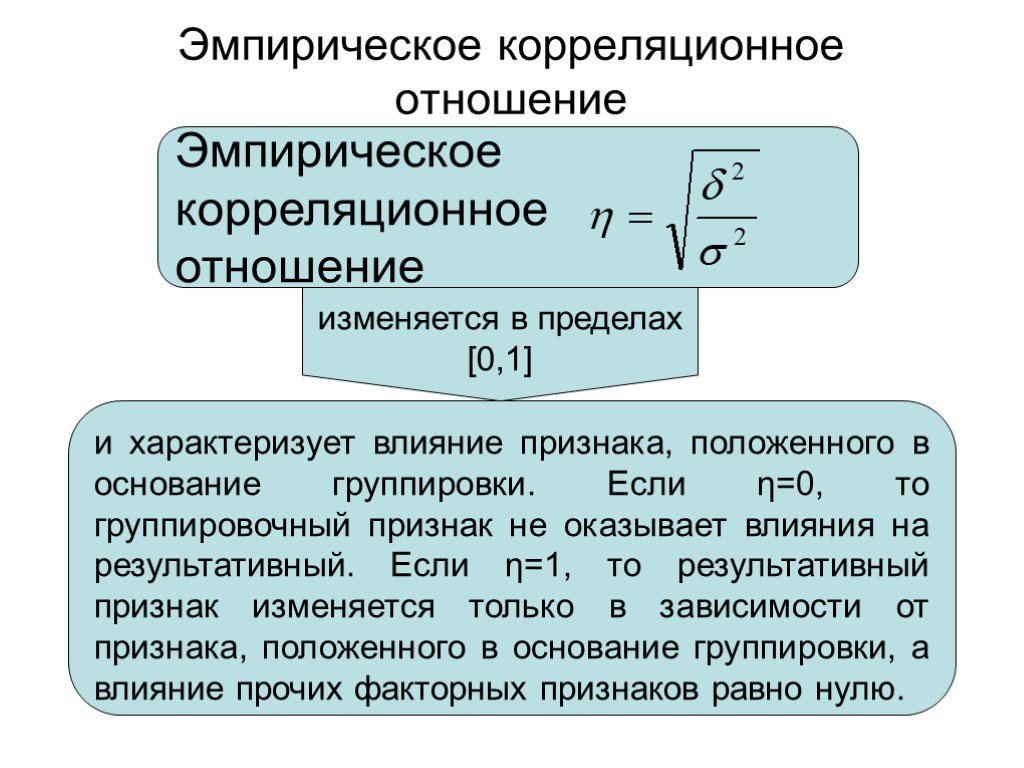
Слайд 42Эмпирическое корреляционное отношение
и характеризует влияние признака, положенного в основание группировки. Если η=0, то группировочный признак не оказывает влияния на результативный. Если η=1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.
изменяется в пределах [0,1]
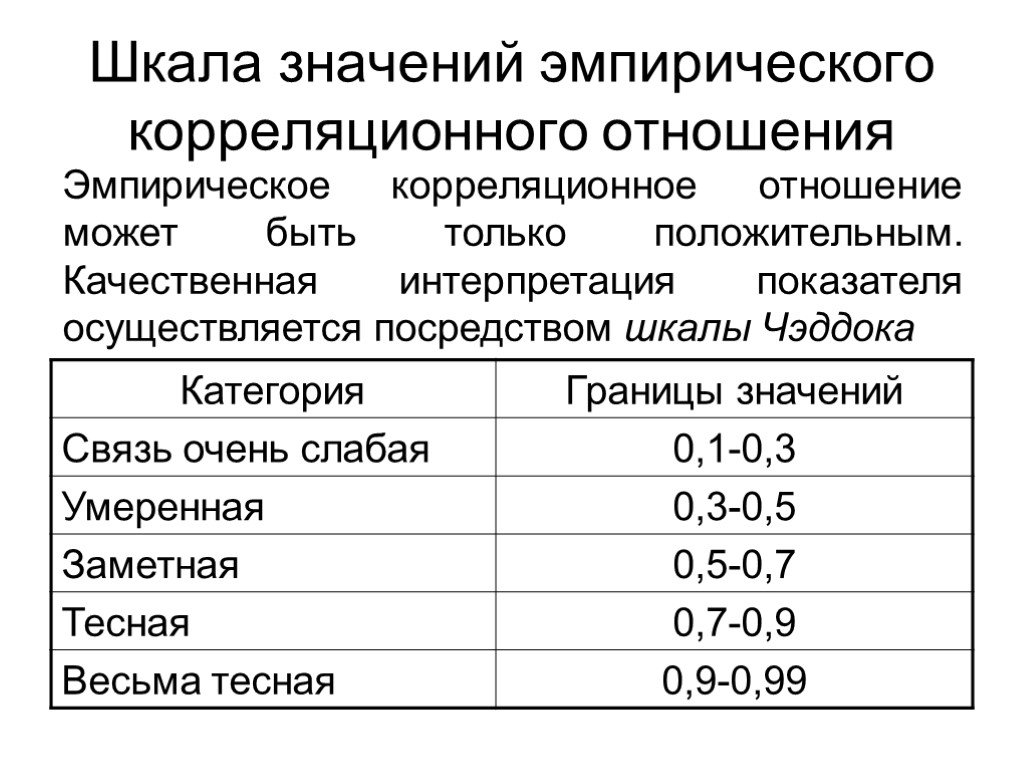
Слайд 43Шкала значений эмпирического корреляционного отношения
Эмпирическое корреляционное отношение может быть только положительным. Качественная интерпретация показателя осуществляется посредством шкалы Чэддока
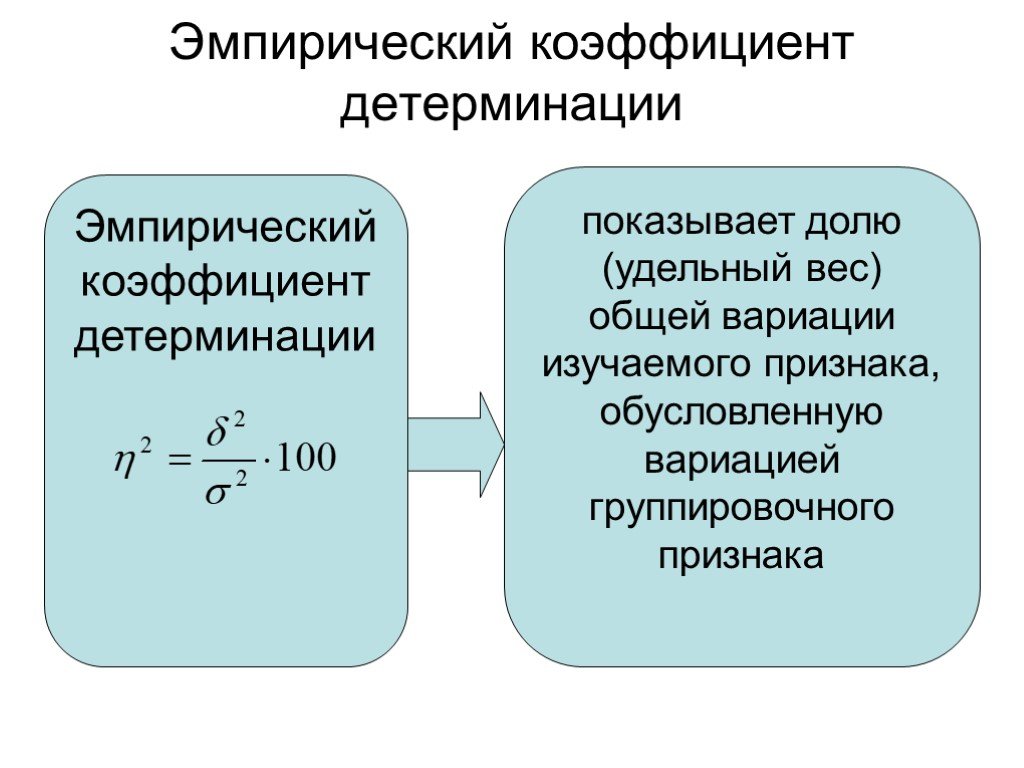
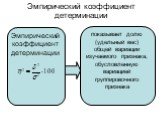
Слайд 44Эмпирический коэффициент детерминации
показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного признака