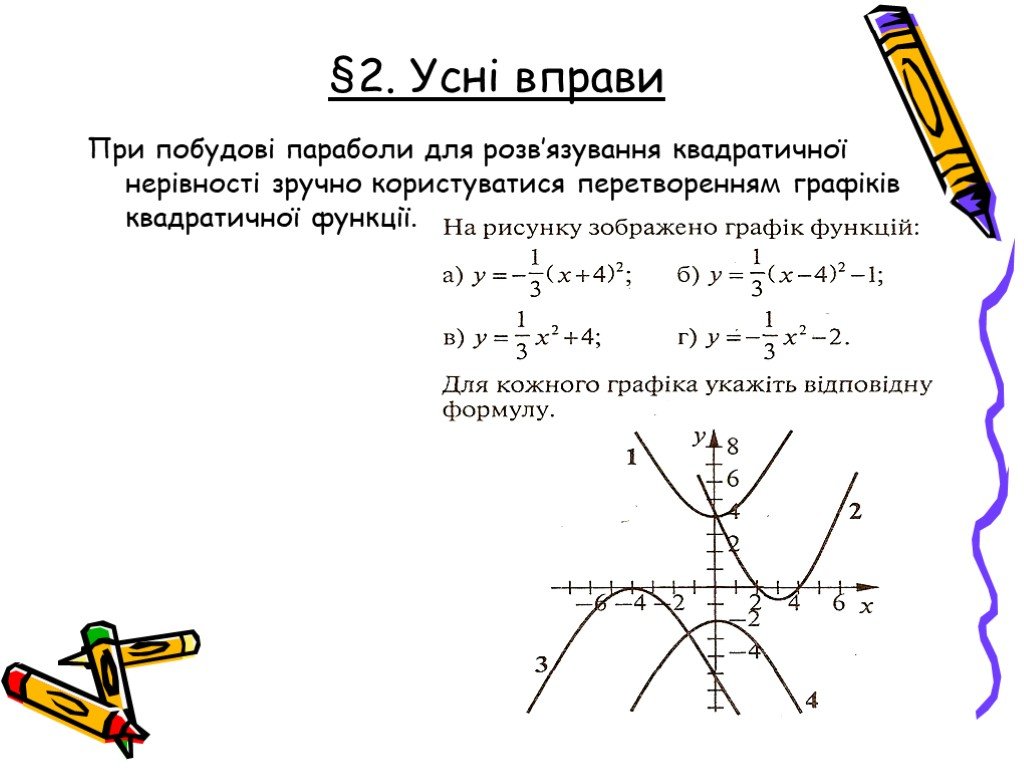
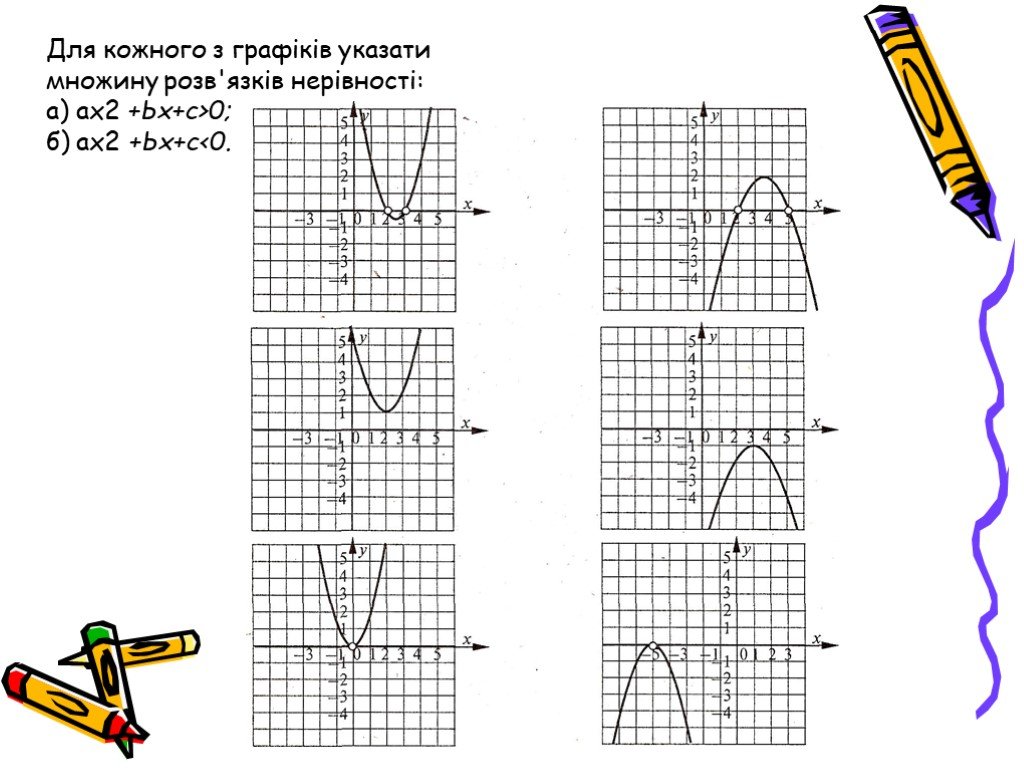
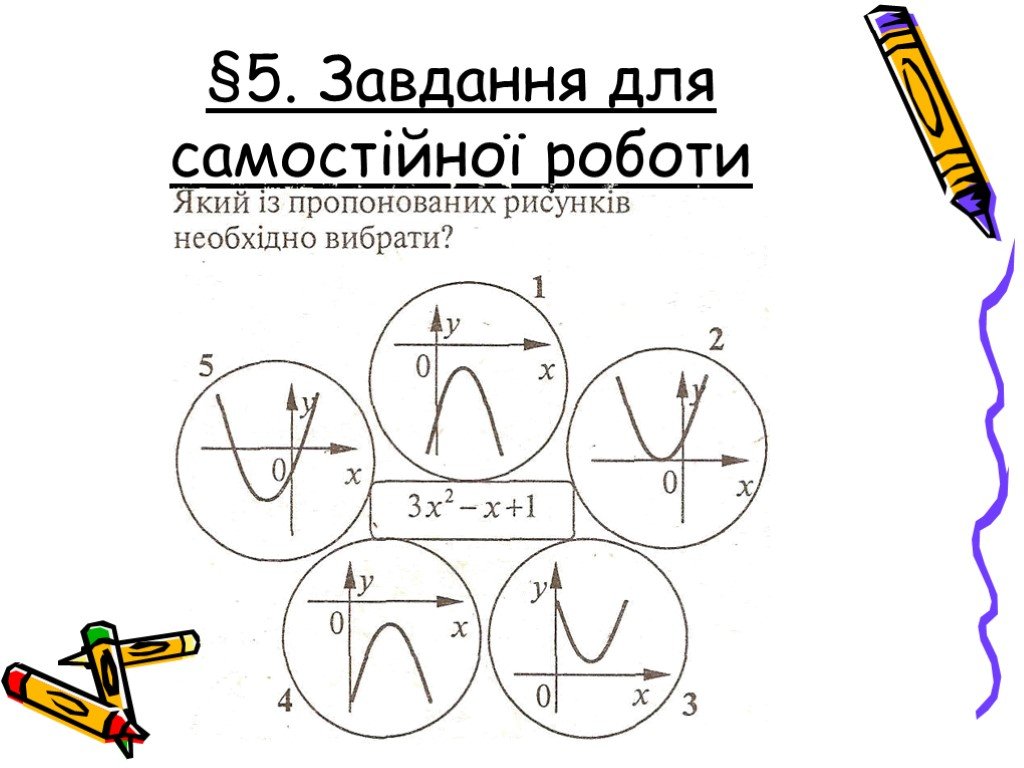
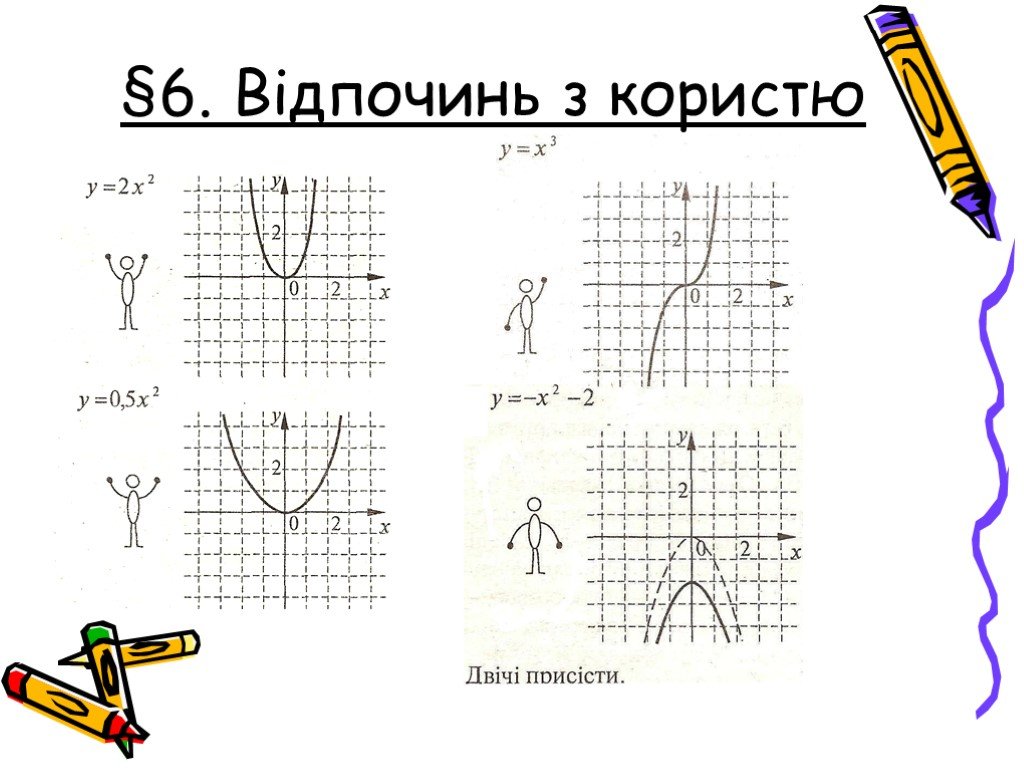
Презентация "Квадратичні нерівності" по математике – проект, доклад
Презентацию на тему "Квадратичні нерівності" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Занимательная математика
РАЗМИНКА Миша тратит на дорогу в школу 5 минут. Сколько минут он потратит на эту дорогу вдвоём с мамой? Какие сто букв могут остановить движение транспорта? ...Занимательная математика
Подводная арифметика. Детёныш голубого кита выпивает за день 600 л молока. Сколько молока выпьет такой малыш за месяц (30 дней)? Ответ: 18 000 л. ...Занимательная математика
Интеллектуальная игра. Играем. Во сколько раз должны некие объекты превосходить остальные, чтобы по праву называться гигантскими? В миллиард раз (гига). ...Занимательная математика
Проблема проекта:. многим ученикам не интересно заниматься математикой. Они считают её сухой и незанимательной наукой, поэтому у них плохие отметки ...Конкурс "Ох, уж эта математика"
Зал красочно оформлен: на стенах математические газеты. Рисунки, кроссворды, высказывания ученых. Их портреты. В жюри трое родителей. Ведущая Счетный ...математика прекрасная наука
let's see what they say about mathematics its great fans and creators. Again and again repeat the saying of Pythagoras: There is no doubt that the ...береза глазами математика
Цель. Целью данного исследования является выявление в повседневной жизни различных законов, которым нас обучают еще в школе. И как же все можно связать ...Занимательная математика для детей (устный счёт + учимся писать цифры)
По дороге мальчик и девочка шли, Оба по два рубля нашли. За ними ещё трое идут. Сколько они денег найдут? Повезло опять Егорке, У реки сидит не зря. ...«Устный счёт» математика
1- 0,4 3 +2,4 3,2 – 2 3,2- 0,2 12,3 + 3,4 2,04 + 3,6 12 – 1,5 6,2- 2,6 ( 12,4 + 3,67)- 2,67 ( 45,06 + 23,5) – 40 ,06. 0,6 5,4 1,2 3 15,7 5,64 10,5 ...Арифметические действия над числами или зачем туристу математика?
27 сентября – день туриста. 34 х 2 = 90 : 30 = 9 + 45 = 11 х 3 = 80 – 19 = 55 : 5 = И У Р Т С 68 3 54 33 61 11. Что лежит в рюкзаке туриста? спички ...«Углы» математика
Цель урока:. познакомить учащихся с геометрической фигурой углом, с видами углов (прямой, тупой, острый), сформировать представления о существенных ...«Своя игра» математика
Математическая игра-викторина «Своя игра». Конец игры Литература. Задачи – шутки 50. Вопрос: Один господин написал о себе: «Пальцев у меня двадцать ...«Своя игра» математика
Условия игры:. Участники сами выбирают темы и вопросы. Вопрос выбирает правильно ответившая команда. 210 – 250 баллов – отметка «5». 110 -200 баллов ...Занимательная математика
Профессор ложится спать в 8 часов вечера и заводит будильник на 9 часов утра. Сколько часов будет спать профессор? Профессор. Рядом с берегом со спущенной ...Веселая математика
1. Разминка «Веселый урок». 2. Конкурс художников. Нарисуйте фигуры, не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии. 3. ...Занимательная математика в младших классах
Круглый, румяный. В печке печён, На окошке стужён. Кто я? Колобок. Проверка 5, 8, 4, 6, 7, 0, 1, 2 Молодцы! Задача. Семь снегирей на ветке сидели. ...Веселая математика
СОДЕРЖАНИЕ Загадки Задачи Ребусы 1 3 4 5 6 7 8 9 10 11 13 14 15. Шёл Кондрат в Ленинград, а навстречу ему пять ребят. Сколько ребят шли в Ленинград? ...Зачем нужна математика
Не хочу я математику учить. Складывать умею, умножать, делить. Сдачу в магазине сосчитаю, Хватит знаний этих, точно знаю. Мне задачи больше не нужны. ...Весёлая математика
Можете ли вы представить сухую, строгую математику занимательной и увлекательной? С трудом? При создании проекта мы поставили перед собой 3 цели: ...Космос и математика
. Открытие космической эры. Открытие космической эры и начало освоения космического пространства - самое выдающееся достижение человечества XX в. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 июня 2019
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию