Презентация "Отображение" по математике – проект, доклад

Движения.

Движением в геометрии называют отображение, сохраняющее расстояния.

Отображения.

Отображением множества M в множество N называется соответствие каждому элементу из M единственного элемента из N. Слово «отображение» означает соответствие точкам точек.

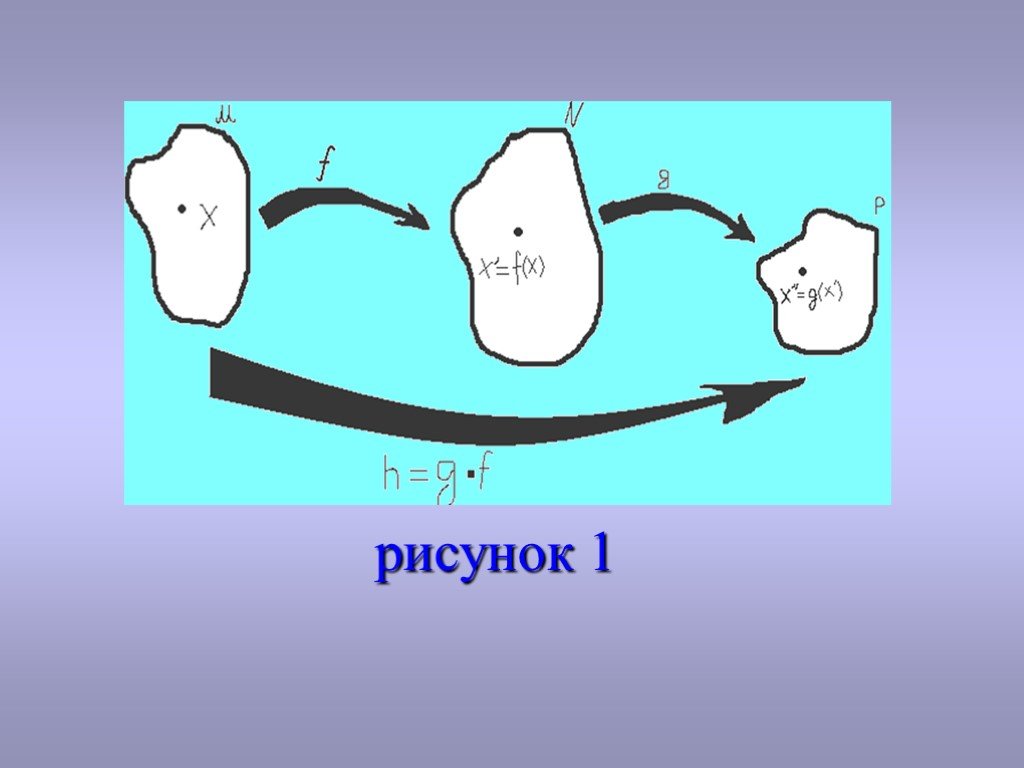
Пусть заданы два отображения: отображение f множества M в множество N и отображение g множества N в множество P. Если при отображении f точка X€M перешла в точку X,=f (X)€N, а затем X, при отображении g перешла в точку X,,€P, то тем самым в результате X перешла в X,,(рис. 1). Это записывается так: X,,=g*f (X). В результате получается некоторое отображение h множества M в множество P. Поскольку при отображении h образом каждой точки X является точка X,,=g*f (X), то пишут, что h=g*f. Отображение h называется композицией отображения f с последующим отображением g. Композицией называется и операция последовательного отображения и результирующее отображение.

рисунок 1

Определение движения.

Замечание: Когда с реальным телом совершают сначала одно, а затем другое движение, то понимают так, что второе движение происходит с тем же телом. В геометрии же это не так!

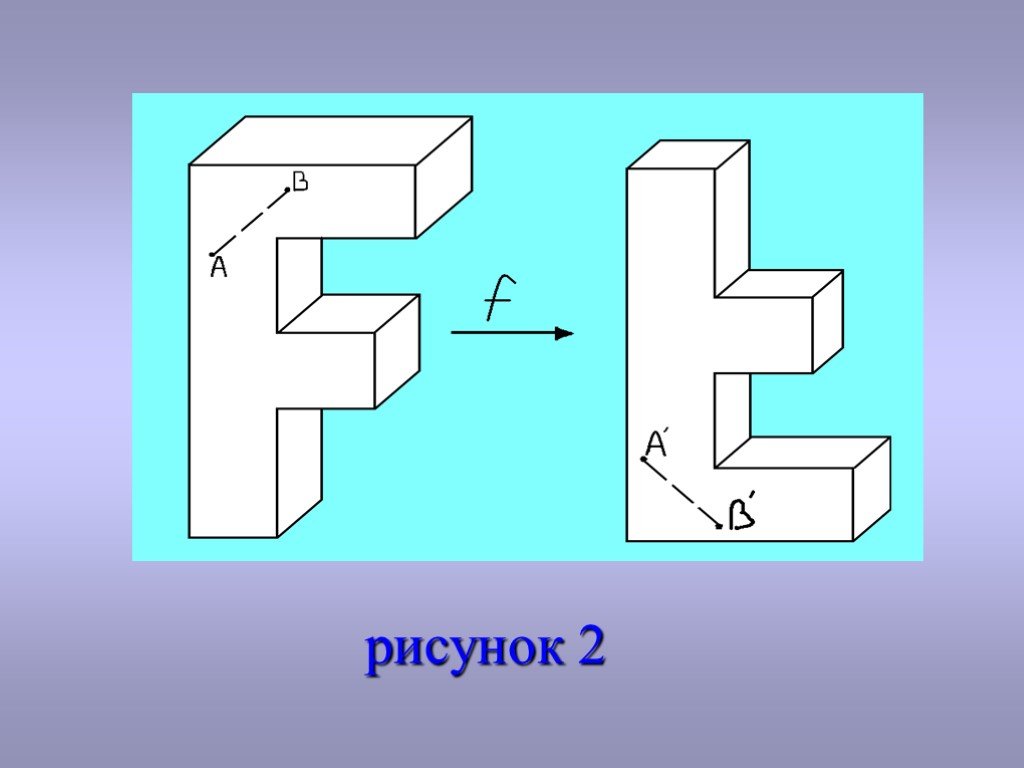
Определение: Движением фигуры называется такое ее отображение, при котором каждым двум ее точкам A,, и B, ,что |A,B,|=|AB|.(рис. 2) Фигура F, называется равной фигуре F, если она может быть получена из F движением. Это и выражено в словах:«фигура F, получается из F движением». Из определений соответствующих понятий непосредственно вытекает: движение взаимно однозначны; движение обратимо и отображение, обратное для движения, является движением; композиция движений движение.

рисунок 2

Общие свойства движений.

С в о й с т в о 1: (сохранение прямолинейности).При движении три точки, лежащие на прямой, переходят в три точки, лежащие на прямой, причем точка, лежащая между двумя другими, переходит в точку, лежащую между образами двух других точек.

Д о к а з а т е л ь с т в о: Из планиметрии известно, что три точки A, B, C лежат на прямой тогда и только тогда, когда одна из них, например точка B, лежит между двумя другими – точками A и C, т. е. когда выполняется равенство |AB|+|BC|=|AC|. (1) При движении расстояния сохраняются, а значит, соответствующее равенство выполняется и для точек A ,, B,, C,: |A,B,|+|B,C,|=|A,C,|. (2) Таким образом, точки A’, B’, C’ лежат на одной прямой и именно точка B’ лежит между A’ и C’. /ч.т.д.

С в о й с т в о 2: Образом отрезка при движении является отрезок.

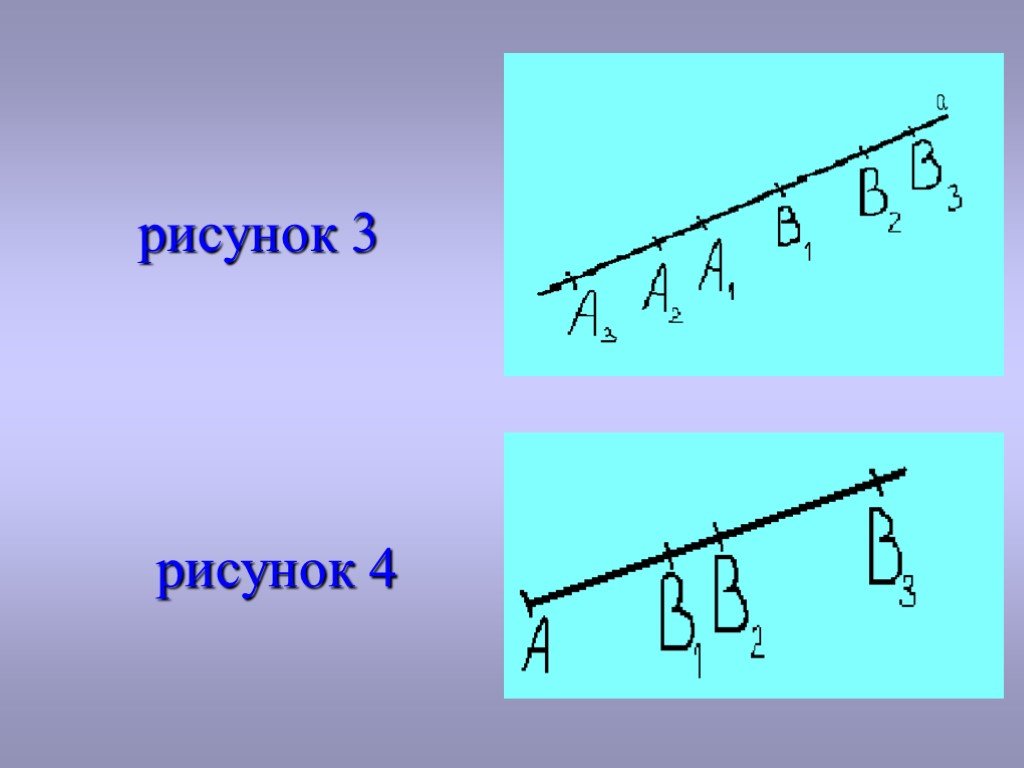
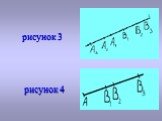
Д о к а з а т е л ь с т в о: Пусть при движении отрезка AB его концы отобразились – A на A’ и B на B’. Любая точка X отрезка AB отобразилась в какую-то точку X’ отрезка A’B’(по свойству 1).При этом образом отрезка AB будет именно весь отрезок A’B’, а не какая-то его часть. В самом деле, любая точка Y’ отрезка A’B’ является образом некоторой точки Y отрезка AB, именно той его точки Y, которая удалена от точки A на расстоянии |A’Y’|. /ч.т.д. С в о й с т в о 3: Образом прямой при движении является прямой, а образом луча – луч. Д о к а з а т е л ь с т в о: Прямая может быть представлена как объединение неограниченно расширяющихся в обе стороны отрезков. A1B1 c A2B2 c A3B3 c ...(рис. 3). Поэтому из свойства 2 следует, что при движении прямая отображается на прямую. Аналогично доказательство верно и для луча (рис. 4)

рисунок 4 рисунок 3

С в о й с т в о 4: При движении образом треугольника является равный ему треугольник, образом плоскости – плоскость, причем параллельные плоскости отображаются на параллельные плоскости, образом полуплоскости – полуплоскость.

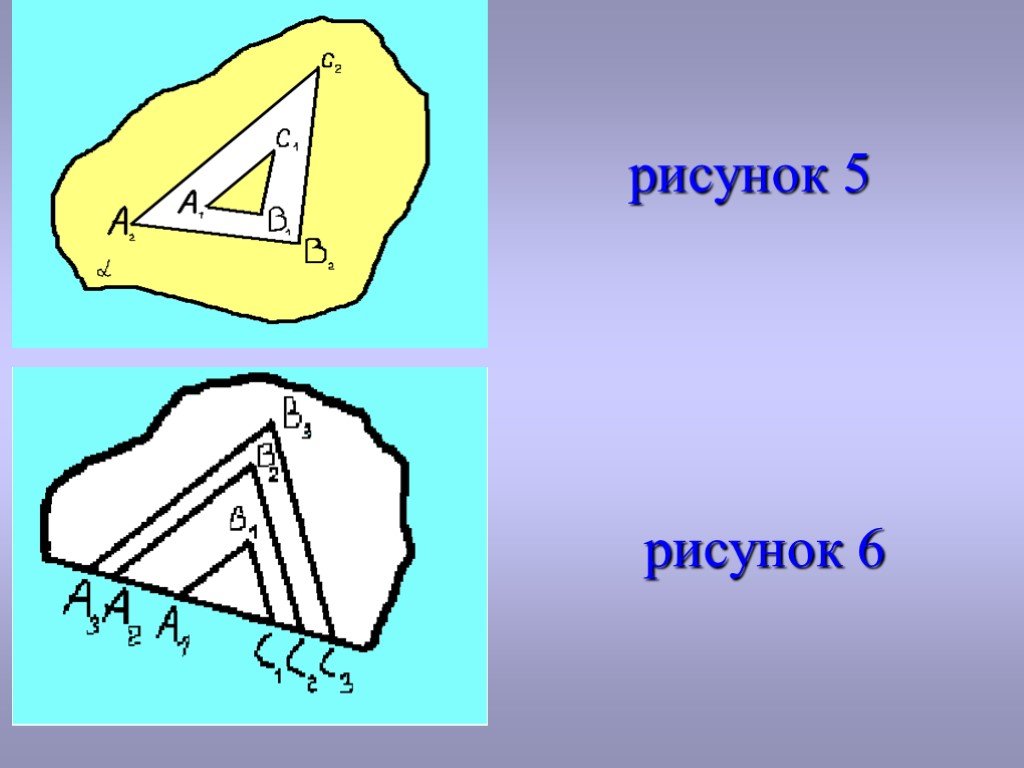
Д о к а з а т е л ь с т в о: Треугольник ABC представляет собой объединение отрезков AX с концами X на отрезке BC. При движении отрезки, и поэтому треугольник отображается на треугольник. Длины сторон сохраняются по определению движения, а углы (точнее, величины углов) сохраняются, так как они выражаются через длины сторон (по теореме косинусов). Плоскость можно представить как объединение неограниченно расширяющихся треугольников (рис. 5). Поэтому при движении плоскость отображается на плоскость (а не на какую-либо ее часть). Полуплоскость можно представить как объединение неограниченно расширяющихся треугольников, у которых одна сторона лежит на прямой (рис. 6). Поэтому полуплоскость отобразится на полуплоскость. Поскольку движение сохраняет расстояния, то расстояние между фигурами при движениях не изменяются. Отсюда следует, в частности, что при движении параллельные плоскости переходят в параллельные./ч.т.д.

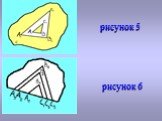
рисунок 5 рисунок 6

С в о й с т в о 5: При движении образом тетраэдра является тетраэдр, образом пространства – все пространство, образом полупространства – полупространство.

Д о к а з а т е л ь с т в о: Тетраэдр PABCD представляет собой объединение отрезков PX с концами X в треугольнике ABC. При движении отрезки отображаются на отрезки, и поэтому тетраэдр отображается на тетраэдр. Пространство можно представить как объединение неограниченно расширяющихся тетраэдров, поэтому при движении пространство отображается на пространство. Полупространство можно представить как объединение неограниченно расширяющихся тетраэдров, у которых основания лежат в граничной плоскости полупространства. Поэтому при движении образом полупространства будет полупространство./ч.т.д.

С в о й с т в о 6: При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины. Аналогичное верно и для двугранных углов.

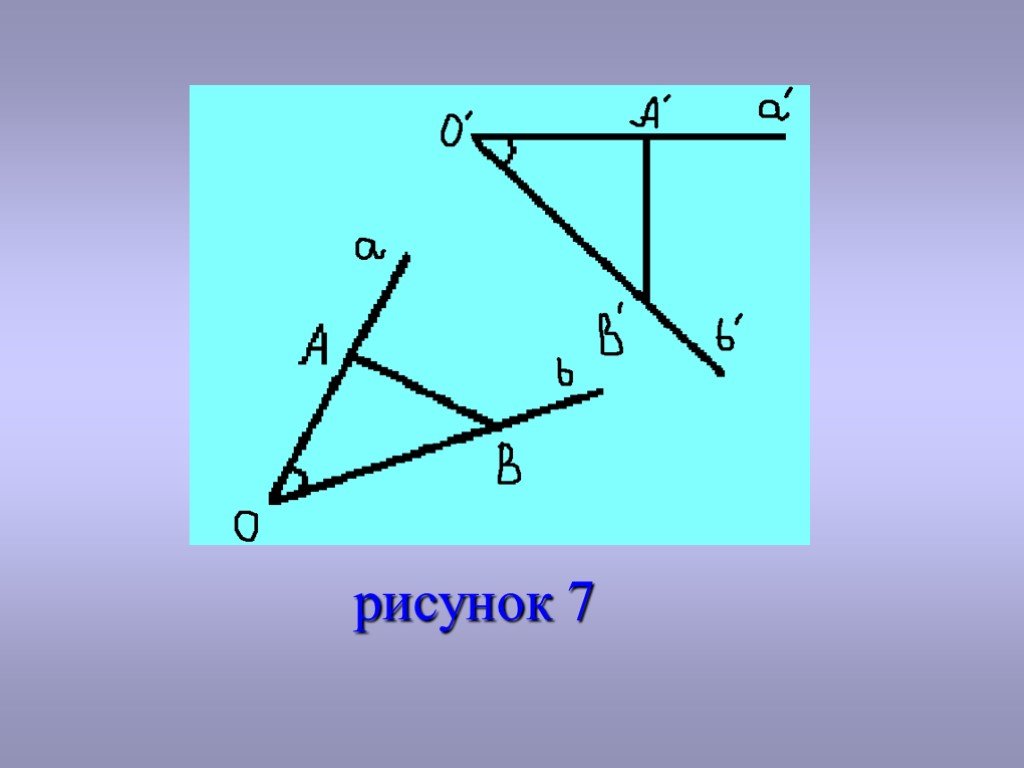
Д о к а з а т е л ь с т в о: При движении полуплоскость отображается на полуплоскость отображается на полуплоскость. Так как выпуклый угол есть пересечение двух полуплоскостей, а невыпуклый угол и двугранный угол есть объединение полуплоскостей, то при движении выпуклый угол переходит в выпуклый угол, а невыпуклый угол и двугранный угол соответственно в невыпуклый и двугранный угол. Пусть лучи a и b, исходящие из точки O, отобразились на лучи a’ и b‘, исходящие из точки O’. Возьмем треугольник AOB с вершинами A € a и B € b (рис. 7).Он отобразится на равный треугольник O’A’ B’ с вершинами A’ € a’, B’ € b’, и, значит, углы между лучами равны. Поэтому при движении величины углов сохраняются. Следовательно, сохраняется перпендикулярность прямых и, значит, перпендикулярность прямой и плоскости. Поэтому, вспоминая определения величины двугранного угла и угла между прямой и плоскостью, получим, что величины этих углов сохраняются./ч.т.д.

рисунок 7

Параллельный перенос.

О п р е д е л е н и е: Параллельным переносом, или, короче, переносом фигуры, называется такое ее отображение, при котором все ее точки смещаются в одном и том же направлении на равные расстояния (рис. 8), т.е. при переносе каждым двум точкам X и Y фигуры сопоставляются такие точки X ’ и Y ’, что XX ’=YY ’ (3)

рисунок 8

Параллельный перенос сохраняет расстояния и направления, т.е. любым двум точкам X и Y соответствуют такие точки X’ и Y ’, что X ’Y ’=XY (4)

1.Параллельный перенос есть движение, сохраняющее направления. 2.Движение сохраняющее направления, есть параллельный перенос. Из этих двух взаимно обратных утверждении непосредственно вытекает, что композиция параллельных переносов есть параллельный перенос. Параллельный перенос фигуры задается указанием одной пары соответствующих точек: если указано, в какую точку переходит данная точка A, то известно, куда переходит любая точка X фигуры; она переходит в такую точку X’ , что XX’=AA’ (5) Можно сказать: перенос задается вектором AA’ , и векторное равенство (5) означает, что все точки смещаются на один и тот же вектор. Следовательно, всякий перенос задается некоторым вектором a, т.е. XX ’=a для всех точек X. Параллельный перенос любой фигуры можно распространить на все пространство, стоит лишь сместить все его точки на тот же вектор, на который смещаются точки фигуры.

Центральная симметрия.

О п р е д е л е н и е: Точки A и A’ называются симметричными относительно точки O, если она делит отрезок AA’ пополам (рис. 9). Точка O считается симметричной сама себе ( относительно O).

рисунок 9

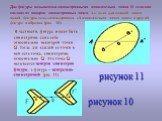
Две фигуры называются симметричными относительно точки o, если они состоят из попарно симметричных точек, т.е. если для каждой точки одной фигуры есть симметричная ей относительно точки точка в другой фигуре и обратно (рис. 10).

В частности, фигура может быть симметрична сама себе относительно некоторой точки O. Тогда для каждой ее точки в ней есть точка, симметрична относительно O. Эта точка O называется центром симметрии фигуры, а фигура – центрально-симметричной (рис. 11).

рисунок 10 рисунок 11

О п р е д е л е н и е: центральной симметрией фигуры с центром O называется такое отображение этой фигуры, которое сопоставляет каждой ее точке точку, симметрично относительно O.

Отношение между симметричными точками взаимное: если A’ симметрична A, то A симметрична A’ относительно того же центра. Поэтому отображение, обратное центральной симметрии всего пространства, есть она же сама. Из определения симметричных друг другу фигур следует, что центральная симметрия с центром в точке O отображает фигуру на симметричную ей относительно точке O. В частности, то, что фигура имеет центр симметрии O, означает, что центральная симметрия с центром O отображает ее на себя.

Основное свойство центральной симметрии содержится в следующей теореме:

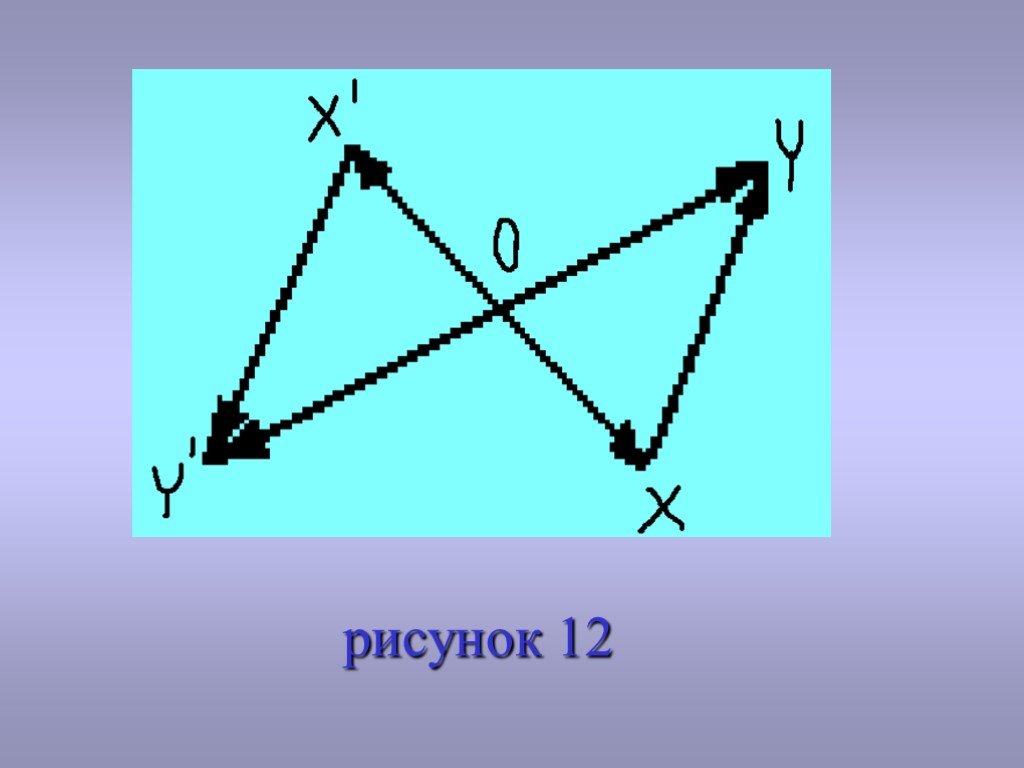
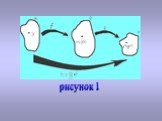
Т е о р е м а: Центральная симметрия сохраняет расстояние, а направления изменяет на противоположные. Иначе говоря, любым двум точкам X и Y фигуры F соответствуют такие точки X ’ и Y ’, что X ’ Y ’= -XY (6). Д о к а з а т е л ь с т в о: Пусть при центральной симметрии с центром в точке точки и отобразились на и . Тогда, как ясно из определения центральной симметрии(рис. 12), OX ’= -OX, OY ’= -OY (7). Вместе с тем XY=OY – OX, X ’Y ’=OY ’- OX’. Поэтому из (7) имеем: X ’Y ’= -OY+OX= -XY. /ч.т.д.

рисунок 12

Теорема: Движение, изменяющее направления на противоположные, есть центральная симметрия.

Центральная симметрия фигуры задается указанием одной пары соответствующих точек: если точка A отображается на A’, то центр симметрии – это середина отрезка AA’. Центральная симметрия любой фигуры естественно распространяется на все пространство: каждой точке сопоставляется симметричная ей относительно того же центра.

Зеркальная симметрия.

О п р е д е л е н и е: Точки A и A’ называются симметричными относительно плоскости a, если отрезок AA’ перпендикулярен этой плоскости и делится ею пополам. Любая точка плоскости a считается симметричной самой себе относительно этой плоскости (рис. 13). Две фигуры F и F ’ называются симметричными относительно данной плоскости, если они состоят из точек, попарно этой плоскости, т.е. если для каждой точки одной фигуры есть симметричная ей точка в другой фигуре. Фигура симметрична относительно данной плоскости и что эта плоскость является ее плоскостью симметрии (рис. 14).

О п р е д е л е н и е: Отображение фигуры, при котором каждой ее точке соответствует точка, симметричная ей относительно данной плоскости, называется отражением фигуры в этой плоскости (или симметрией относительно этой плоскости)

Если A’ симметрична A относительно плоскости a, то A симметрична A’ относительно той же плоскости a. Поэтому отображение, обратное отображению в плоскости всего пространства, есть оно само. Ясно, что при отображении фигура отображается на симметричную ей фигуру относительно этой плоскости. Теорема: Отображение в плоскости сохраняет расстояния и, стало быть, является движением. При отражении в плоскости все точки ее неподвижны, т.е. отображаются сами на себя. Теорема: Движение, при котором все точки некоторой плоскости неподвижны, является отображением в этой плоскости или тождественным отображением. Д о к а з а т е л ь с т в о: Пусть при движении все точки плоскости a, неподвижны. Тогда из сохранения углов и расстояний следует, что , прямые, перпендикулярные a, отображаются на себя. При этом либо точки отображаются в a, либо все точки неподвижны. / ч.т.д. Отражение в плоскости задается указанием одной пары соответствующих точек, на лежащих в плоскости симметрии.