Презентация "СТАРИННЫЕ ЗАДАЧИ НА ДРОБИ" по математике – проект, доклад

СТАРИННЫЕ ЗАДАЧИ НА ДРОБИ

Открытый урок учителя математики 1 категории Черновой Галины Петровны

Цель урока: решение задач, взятых разных источников.

Задачи : Проверить устный счет на работе с обыкновенными дробями; Решить несколько задач вместе с разбором на доске; Провести самостоятельную работу на решение задач.

Устный счет

Задачи на смекалку

Старинная задача. Работали два крестьянина в поле и решили пообедать. У первого было два хлеба, а у второго- один В это время подошёл к ним третий и попросил поделиться. Ему дали один хлеб и каждый съел по хлебу. За свою долю крестьянин дал им 6 рублей и, поблагодарив, ушёл. Как поделить оставшимся эти деньги?

Построить ломаную из четырёх звеньев, проходящую через все девять точек.

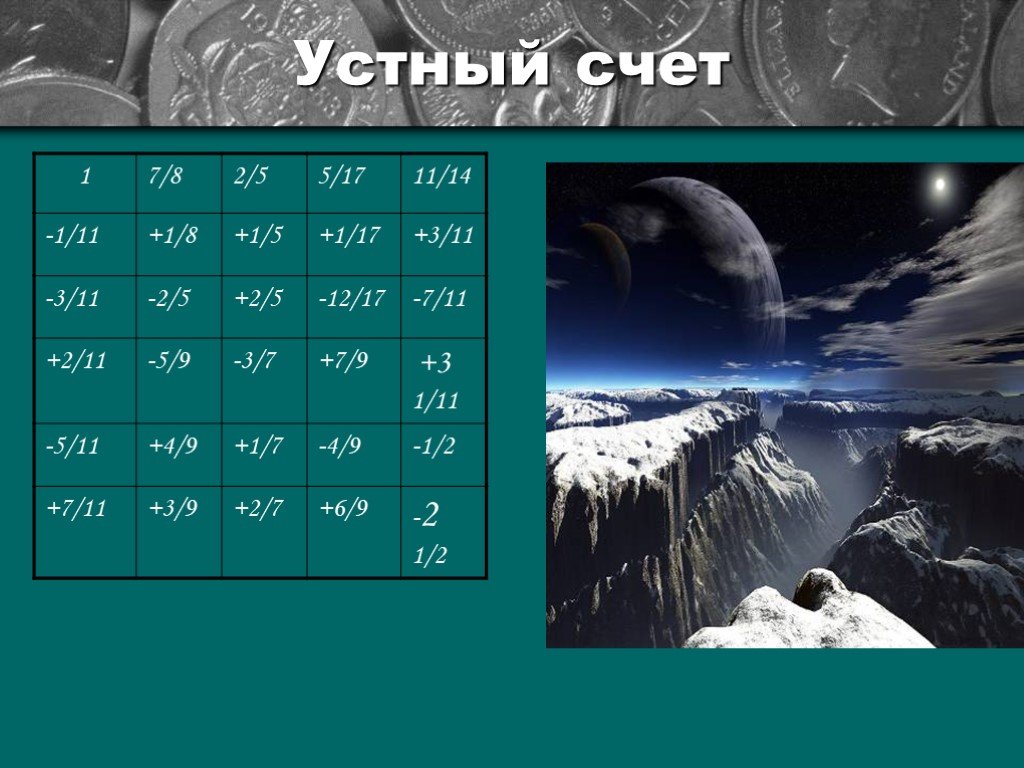
Математический тренажёр

Старинные задачи

В древних рукописях и старинных учебниках арифметики разных стран встречаются много интересных задач на дроби. Решение каждой из таких задач требует немалой смекалки, сообразительности и умения рассуждать. Рассмотрим несколько таких задач.

задачи

Путник, догнав другого, спросил его: «Далеко ли до деревни, которая впереди?» Другой путник ответил: « Расстояние от деревни, из которой ты идёшь, равно трети всего расстояния меду деревнями. А если пройдёшь ещё две версты, будешь ровно посередине между деревнями. Сколько вёрст осталось идти первому путнику?

Четыре плотника хотят построить дом. 1 плотник может построить дом за год, второй- за 2 года, третий- за три года, четвёртый- за 4 года. За сколько лет они построят дом при совместной работе? «Арифметика», Магницский, 1703

2 версты, которые нужно пройти до середины, составляют 1/6 всего расстояния до деревни. 2*6=12( вёрст) всё расстояние 12*1/3=4( версты) прошёл путник 12-4=8 (вёрст) осталось Ответ: 8 вёрст.

Число 12 –делители 1, 2, 3, 4. 1) 12:1=12( домов) 1 плотник за 12 лет 2) 12:2=6( дом) 2 плотник за 12 лет 3) 12:3=4( дом) 3 плотник за 12 лет 4) 12:4=3( дом) 4 плотник за 12 лет 5) 12+6+4+3=25( домов) вместе за 12 лет 6) 12:25= 12/25( года) 1 дом вместе. Ответ: примерно 6 месяцев.

Из папируса Ахмеса (Египет, ок. 2000 лет до н.э.).

Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты из своего многочисленного стада? Пастух отвечает: - Я привожу две трети от трети скота. Сочти, сколько быков в стаде?

Решение: 70 быков составляют 2/3 от1/3 1) 2/3*1/3=2/9 составляют 70 быков. 2) 70 : 2/9= 315(быков) составляют стадо. Ответ: 315 быков

Китай, II век н.э.

Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моя до южного моря летит 9 дней. Теперь утка и гусь вылетают одновременно. Через сколько дней они встретятся?

Решение: утка 7 дн. 9раз 63 дня гусь 9 дн. 7раз 63 дня 1)7+9=16 раз 2) 63:16= 3 15/16 ( дней) 1) 1:7=1/7пути утка 1 д. 2) 1:9=1/9пути гусь 1 д. 3) 1/7+1/9=16/63 вместе 4) 1:16/63=3 15/16 дней Ответ: через 3 15/16 дней.

Из книги «Косс» Адама Ризе (XVI в.)

Трое выиграли некоторую сумму денег. На дою первого пришлось ¼ этой суммы, на долю второго -1/7, а долю третьего – 17 флоринов. Как велик весь выигрыш?

Решение: примем выигрыш за 1. 1) ¼+1/7=11/28(ч.) выиграли двое 2)1-11/28=17/28(ч.) выиграл третий 3)17/28=11/28 17 флористов есть 11/28 4)17:17*28=28(флор.) Ответ: 28 флоринов весь выигрыш.

В знаменитой книге «1001 ночь» мудрец задаёт юной деве следующую задачу:

Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся. Так же она поступила и с третьим стражником, а когда она поделилась яблоками с четвёртым стражником, у неё осталось 10 яблок. Сколько яблок она собрала в саду?

Решение: I способ: 1) 1-1/2=1/2(ч) осталась 2) 1/2-1/4=1/4(ч) осталась 3) 1/4-1/8=1/8(ч) осталась 4) 1/8-1/16=1/16(ч) осталась 1/16 составляет 10 яблок 5) 10*16=160(яблок) IIспособ: 1)2*2*2*2=16(раз) 2)10*16=160(яблок) III способ: 1) 10*2=20(яблок) 2) 20*2=40(яблок) 3) 40*2=80(яблок) 4) 80*2=160(яблок) Ответ: 160 яблок.

Брахмагупта, Индия, около 600 г.

Слон, слониха и слонёнок пришли напиться к озеру, чтобы напиться воды. Слон может выпить озеро за 3ч, слониха - за 5ч, а слонёнок - за 6ч. За сколько времени они все вместе выпьют озеро?

Решение: Слон - 1 озеро 3ч 10 озёр 30ч Слониха- 1 озеро 5ч 6 озёр 30 ч. Слонёнок- 1 озеро 6ч 5 озёр 30 ч. НОК(3,5,6)=30 1)10+6+5=21(озеро) выпьют слон, слониха и слонёнок за 30часов, 2)30:21=1 3/7(ч) они вместе выпьют озеро. Ответ:1 3/7 часа.

Из «Арифметики» Магницкого (Россия, XVIII в.)

Решение: Лошадь- 1 воз 1 месяц 6 возов- 6месяцев Коза- 1 воз 2 месяца 3 воза- 6 месяцев Овца- 1 воз 3 месяца 4 воза- 6 месяцев НОК(1,2,3)=6 1)6+3+4=11(возов) лошадь, коза и овца за 6 мес. 2)6:11=6/11(месяца) они съедят 1 воз. Ответ: 6/11 месяца.

Лошадь съедает воз сено за месяц, коза- за два месяца, овца- за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Из Акмимского папируса (VI в.)

Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял 1/17. Оставил же в сокровищнице 192. Мы хотим узнать, сколько было в сокровищнице первоначально?

Решение: 1)1-1/13=12/13(ч) сокровищ осталось 2)12/13-1/17=191/221(ч) сокровищ осталось 191/221 составляет 191 3)191:191*221=221 Ответ: 221 было первоначально.

Домашнее задание

Древняя Греция, Герон Александрийский, I в. до н.э. Бассейн может заполняться через четыре фонтана. Если открыть только первый фонтан, бассейн наполнится за день, только второй- за два дня, только третий- за три дня, только четвёртый- за четыре дня. За какое время наполнится бассейн, если открыть все четыре фонтана?

Итог урока

Задачи, разобранные и решенные на этом уроке, были взяты из древних рукописях и старинных учебниках, некоторые из них можно было решить традиционными способами, но мы рассматривали и другие красивые способы решения, предложенные древними учеными и математиками. При решении задач важно уметь логически рассуждать, знать, как правильно работать с обыкновенными дробями, ведь они встречаются в предложенных задачах. Для тех, кто увлекается математикой, этот урок обязательно понравится.