Презентация "Логика" (9 класс) по информатике – проект, доклад
Презентацию на тему "Логика" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Логика и русский язык
Проверка домашнего задания. Работа за компьютером. Программа «Страна фантазия». Угадай словечко. В группе слов найди лишнее слово и вычеркни его. ...Логика и математика
Разминка. Знают дети всего мира: Робот – умная машина. Может он решать задачи, Может он стихи писать. Может робот печь печенье, Может он варить варенье, ...Примеры заданий по теме "Логика"
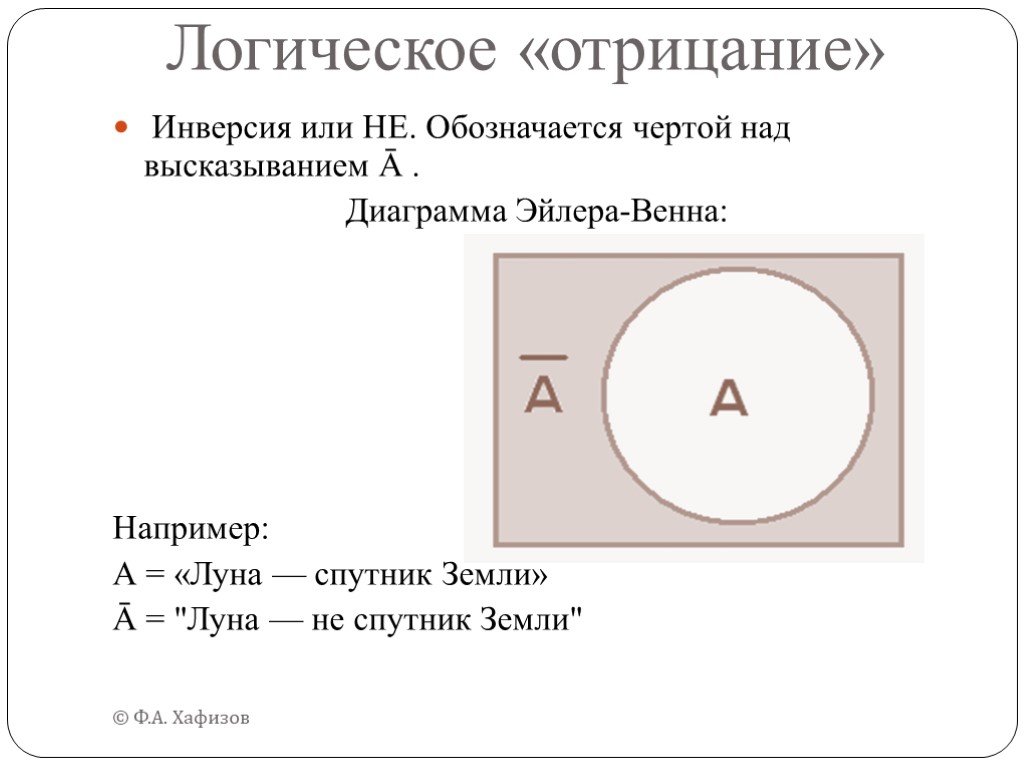
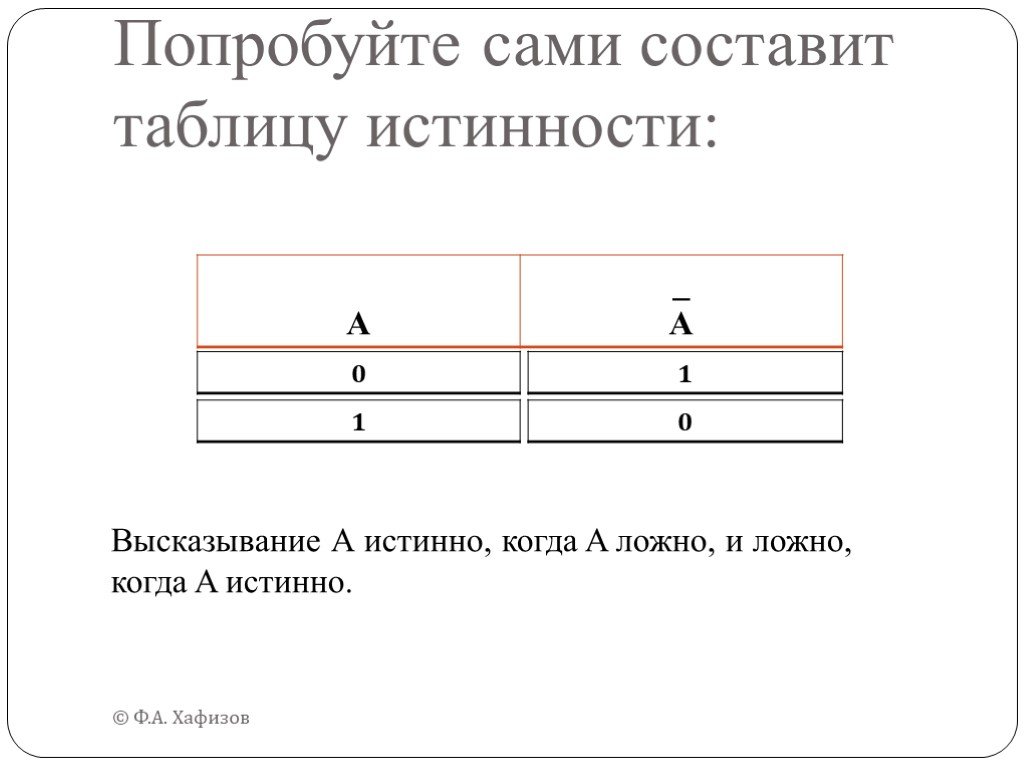
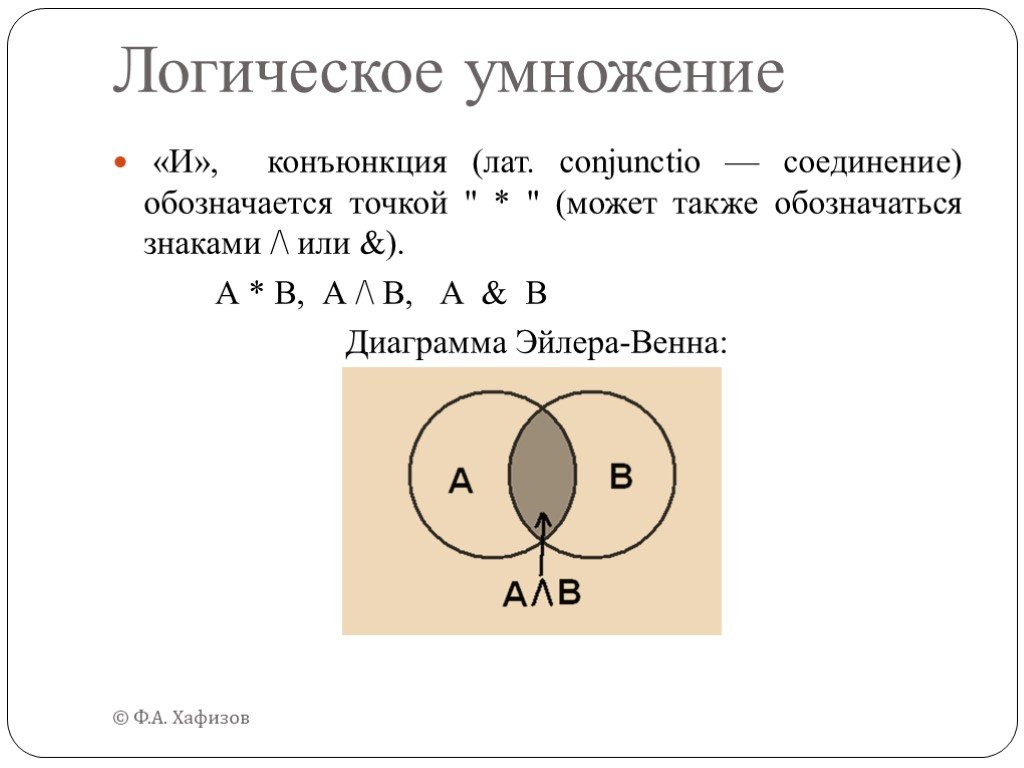
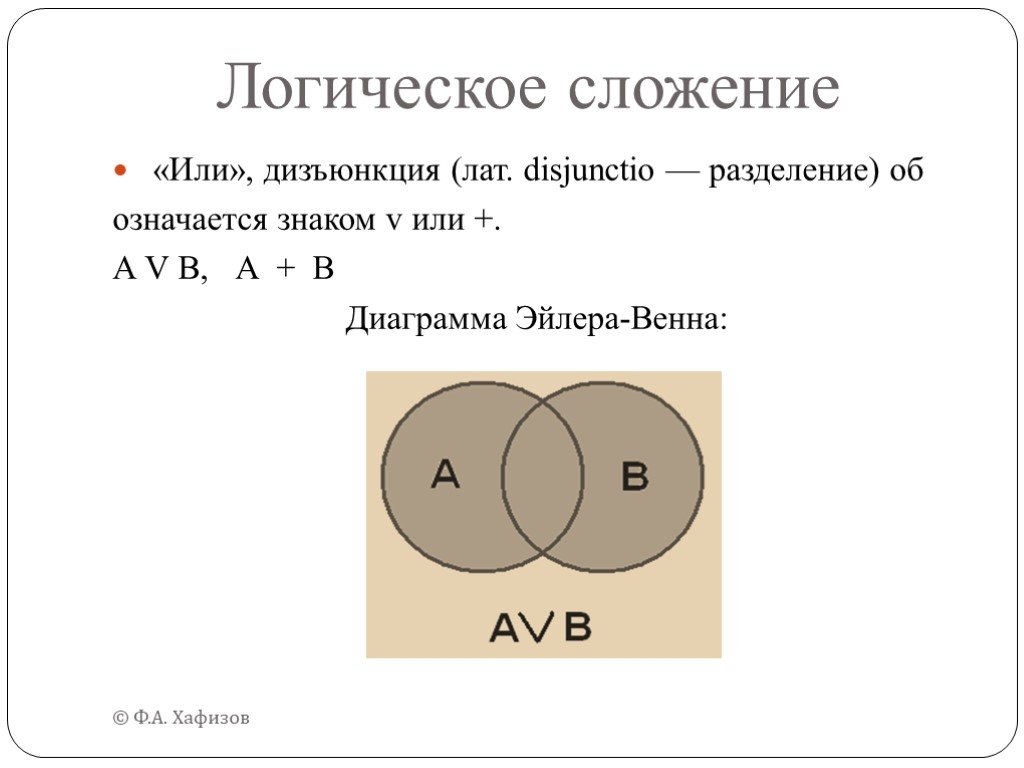
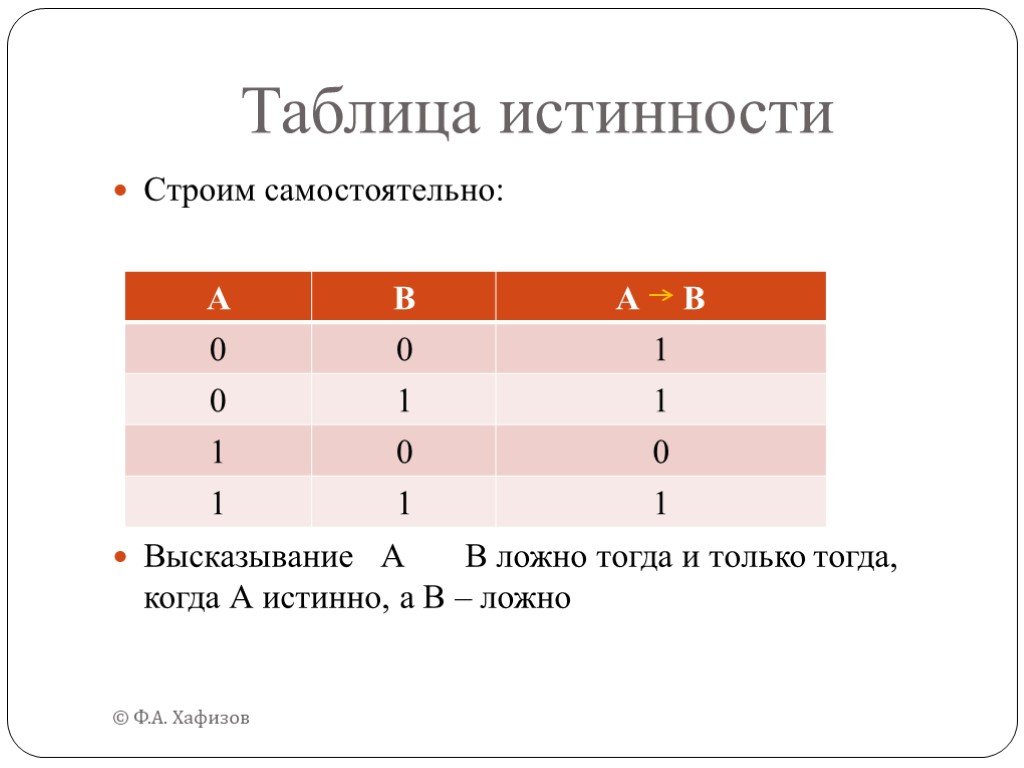
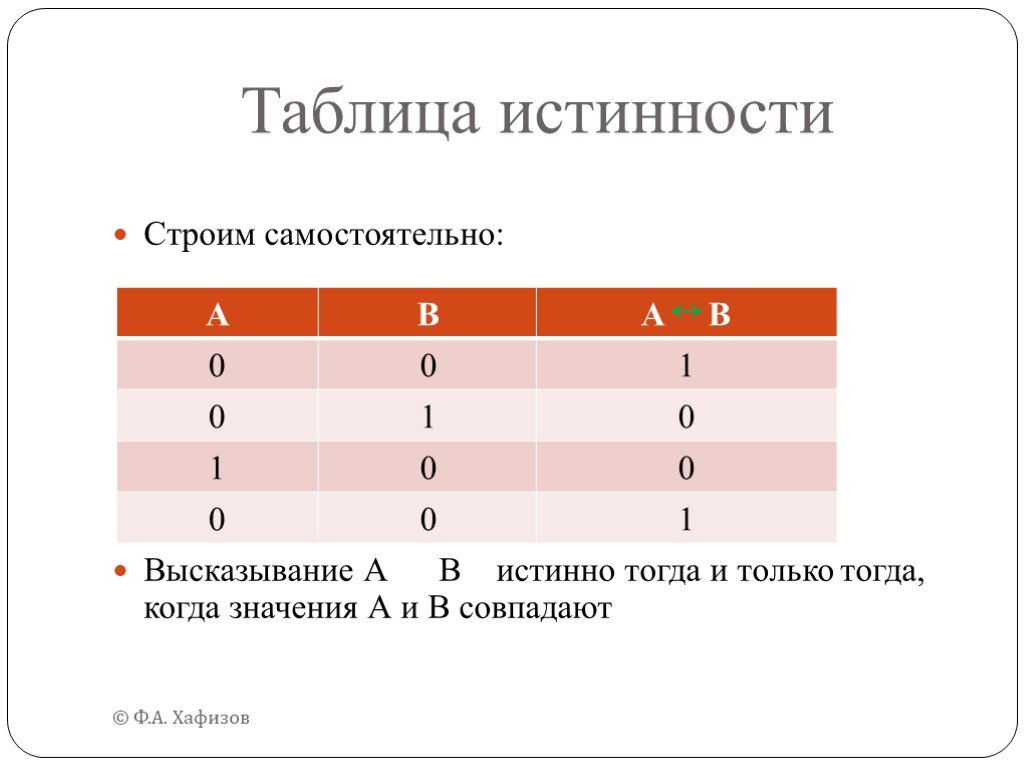
Дан фрагмент таблицы истинности функции F (см. таблицу 1). Какое из перечисленных выражений соответствует F А→¬Aν¬B 3. ¬A→B 2. AνB 4. ¬AΛ¬B. Решение: ...Логика и логические операции
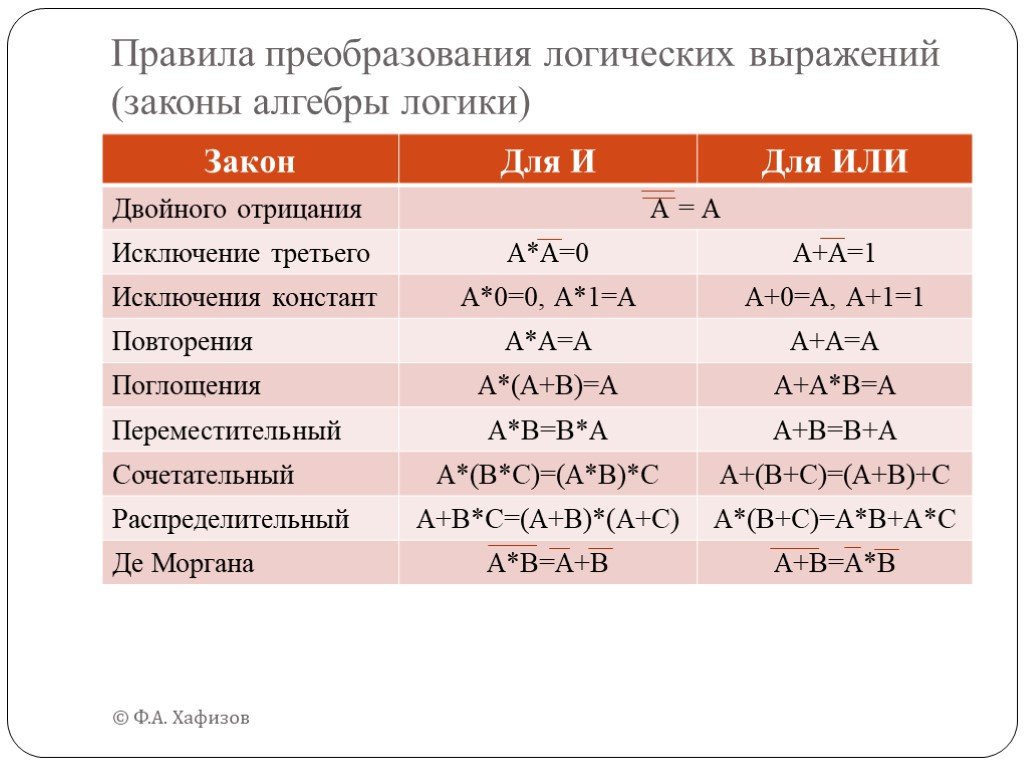
История логики. Логика – наука о формах правильного мышления (рассуждения). Термин происходит от греческого слова «логос», что значит рассуждение. ...Логика и алгоритмы
Кодификатор элементов содержания и требований к уровню подготовки выпускников ОУ для ЕГЭ 2010 года. Спецификации КИМ ЕГЭ 2010 года. Обобщенный план ...Логика высказываний. Алгоритм построения
Таблицы истинности. Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое ...Тест Алгоритмизация и программирование
В этой презентации приводятся тренировочные задания из нескольких источников: открытого сегмента федерального банка тестовых заданий, демонстрационных ...Социальная информатика
Социальная информатика - это наука, изучающая комплекс проблем, связанных с прохождением информационных процессов в социуме. Один из основоположников ...Социальная информатика
Социальная информатика - это про что? Обратимся к предметной области Информатикa. Социальная информатика. Информационные ресурсы как фактор социально-экономического ...Параллельное программирование WinAPI и OpenMP 7
Литература. 1. И. Одинцов Профессиональное программирование. Системный подход. – «БХВ-Петербург» - 2004. – 610 с. 2. Джин Бэкон, Тим Харрис Операционные ...Прикладная информатика
Профессиональный стандарт. Исследователь в сфере ИТ - Computer and Information Scientist, Research Программист - Computer Programmer Системный архитектор ...Что такое программирование
Назначение программирования- разработка программ управления компьютером с целью решения различных информационных задач. Специалисты, профессионально ...Алгоритмизация и программирование в Pascal
Вводная часть. Процесс решения задачи на ПК – это совместная деятельность человека и машины. Его условно можно разделить на несколько этапов. Человеку ...Нелинейное программирование
Отличия от ЗЛП: 1. ОДЗ не обязательно выпуклая. 2. Экстремум не обязан находится на границе ОДЗ. - задача классической оптимизации. Пример:. . Метод ...Объектно-ориентированное программирование
Содержание:. Графы: определения и примеры Ориентированные графы Путь в орграфе Матрица смежности Иерархический список Алгоритм Дейкстры Программа ...Введение в объектно-ориентированное программирование
X, Y – координаты центра круга;. Draw R – радиус круга; Color – цвет круга. 1 способ. Draw1: R=10; x=5; y=10; color=3; Draw2: R=45; x=15; y=3; color=2;. ...Введение в параллельное программирование
Содержание лекции. Формальный подход к определению параллельной программы Меры качества параллельных программ Предел ускорения вычислений при распараллеливании ...Бизнес информатика
Бизнес-информатика — междисциплинарное направление практической и теоретической деятельности, исследований и обучения, затрагивающее вопросы бизнес-управления, ...Аспектно-ориентированное программирование
Сквозная функциональность. Ведение журналов Авторизация. Модуль оформления заказов. Модуль принятия товаров. Проблемы сквозной функциональности. Запутанность ...Алгоритмы и программирование
АЛГОРИТМ Линейный Циклический С ветвлением С процедурой. Программа – запись алгоритма на языке программирования для компьютера. Алфавит языка. Алфавит ...Конспекты
Логика
. Автор разработки: Матюнькина Светлана Васильевна. . Место работы: МБ ОУ Арзинская СОШ, Починковского района, Нижегородской области. . Должность ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 ноября 2018
Категория:Информатика
Классы:
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию