Презентация "Метод группового учёта аргументов" по информатике – проект, доклад
Презентацию на тему "Метод группового учёта аргументов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Математическое моделирование. Численные методы и использование ЭВМ в решении прикладных задач
Процесс мат. моделирования. Систематизация. Реальная ситуация. Сбор данных. Постановка задачи. Физическая модель. Декомпозиция. Математическая модель. ...Метод потенциальных функций
Метод потенциальных функций связан со следующей процедурой. В процессе обучения с каждой точкой пространства изображений, соответствующей единичному ...Программное обеспечение учёта рабочего времени универсального
Назначение. Сбор и обработка информации об ОШС организации и событий прихода/ухода сотрудников; Учёт рабочего времени сотрудников; Анализ рабочего ...Метод остаточных векторов в MSC
Раздел 11. Метод остаточных векторов. ИДЕЯ МОДАЛЬНОГО ПОДХОДА..……………………………..……… 11 - 3 СПОСОБЫ КОМПЕНСАЦИИ ОТСУТСТВИЯ МОД………………….... 11 - 5 ОСТАТОЧНЫЙ ...Метод координат, как форма представления информации
Выполните задание:. На координатной плоскости отметьте и пронумеруйте точки, координаты которых приведены дальше. Соедините точки в заданной последовательности. ...Метод координат
Прямоугольная декартовая система координат. по имени французского математика Рене Декарта. Любая информация , в том числе и графическая, может быть ...Метод координат
О 1 Y X. Рене Декарт (1596 – 1650). . . . 5 10. 1(4, 1), 2(4, 2), 3(1, 2), 4(4, 5), 5(2, 5), 6(4, 7), 7(3, 7), 8(5, 9), 9(7, 7), 10(6, 7), 11(8, ...Метод базовых алгоритмов
За результатами виконання тесту з математики учнями 4-х класів загальноосвітніх навчальних закладів України, на початковому рівні засвоїли програмовий ...Информационное моделирование как метод познания
Цель: Сформировать понятие моделирования как метода познания; рассмотреть различные классификации моделей; сформировать понятие «информационная модель». ...Простейшие методы шифрования текста
Общество, в котором живёт человек, на протяжении своего развития имеет дело с информацией. Она накапливается, перерабатывается, хранится, передаётся. ...Статистические методы обработки информации
Статистика - отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) ...Бездеформационные методы колебаний в MSC
Раздел 5. Бездеформационные моды колебаний. БЕЗДЕФОРМАЦИОННЫЕ МОДЫ И ВЕКТОРЫ. АСПЕКТЫ ТЕОРИИ……………… 5 - 3 ВЫЧИСЛЕНИЕ БЕЗДЕФОРМАЦИОННЫХ МОД.………………………………………. ...Базовые топологии и методы доступа к ЛВС
Физическая передающая среда. Витая пара. неэкранированная витая пара. Максимальное расстояние, на котором могут быть расположены компьютеры, соединенные ...Инженерно-технические методы и средства защиты информации
Это физические объекты, механические, электрические и электронные устройства, элементы конструкций зданий, средства пожаротушения и др. обеспечивают: ...Методика изучения темы "Алгоритмизация и программирование"
Основные понятия, которые с которыми учащиеся знакомятся в курсе изучаемого раздела это - алгоритм, исполнитель алгоритма, система команд исполнителя, ...Вирусы шифровальщики и методы борьбы с вирусами
Оглавление:. 1. Вирусы Шифровальщики - Чем они опасны и с чем их едят 2. Способы борьбы с вирусами 3. мы надёжно защищены от вирусов ? Вирусы Шифровальщики. ...Объектная модель Microsoft Office. Основные объекты и их свойства и методы
Содержание:. СОСТАВ И НАЗНАЧЕНИЕ MICROSOFT OFFICE ТЕКСТОВЫЙ РЕДАКТОР WORD EXCEL POWERPOINT ACCESS Outlook Express Publisher InfoPath. СОСТАВ И НАЗНАЧЕНИЕ ...Алгоритмы и методы поиска событий в видео потоке
Цели доклада. Рассмотреть основные имеющиеся алгоритмы поиска событий Указать на их недостатки Указать направление поиска решения некоторых проблем ...Объекты и их свойства информатика
Объект - ЯБЛОКО красное круглое вкусное висит съедается продается зеленое кислое. о нем рассказывают. Объект - КНИГА листать читать. закрывать закладывать. ...Объектно-ориентированное программирование
основано на принципах логического вывода из базы знаний – фактов и правил. Логическое программирование. основано на принципе последовательной детализации ...Конспекты
Способы кодирования информации. Метод координат
Открытый урок в 5 классе. «Способы кодирования информации. Метод координат». Цель урока:. показать детям многообразие кодов в окружающем мире;. ...Формы представления информации. Метод координат
Муниципальное общеобразовательное учреждение. «Пятницкая средняя общеобразовательная школа». Волоконовского района Белгородской области. ...Метод координат
Урок по информатике в 5 классе. по теме: «Метод координат». Автор- Хужаева Зульфия Растямовна, учитель информатики МБОУ «Яксатовская СОШ» Приволжского ...Метод координат
Технологическая карта урока. Предмет___. _______ИнформатикаКласс_____________5. Автор УМК_______Босова Л. Л.Тема урока________ «Метод ...Метод координат
. Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №4. г. о. Стрежевой. Тема урока:. . «. Метод ...Метод координат
Тема урока «Метод координат». 5 класс. Цель:. Обучающая:. Закрепить знания обучающихся по теме «Метод координат». . Закрепить основные ...Метод координат
Технологическая карта урока. Босова. Информатика . 5 класс. ФГОС. Урок 9. Метод координат. Цели урока:. . . -систематизировать и обобщить сведения, ...Метод координат
Муниципальное бюджетное общеобразовательная учреждение. «Манжерокская средняя общеобразовательная школа». Урок информатики ...Кодирование информации. Формы представления информации. Метод координат
Муниципальное общеобразовательное учреждение. «Северная средняя общеобразовательная школа № 2. Белгородского района Белгородской области». ...Кодирование информации. Метод координат
5 класс Урок № 9. . Тема урока:. . «Кодирование информации. Метод координат». Цели урока. :. . Углубить представление учащихся о формах ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 марта 2019
Категория:Информатика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию







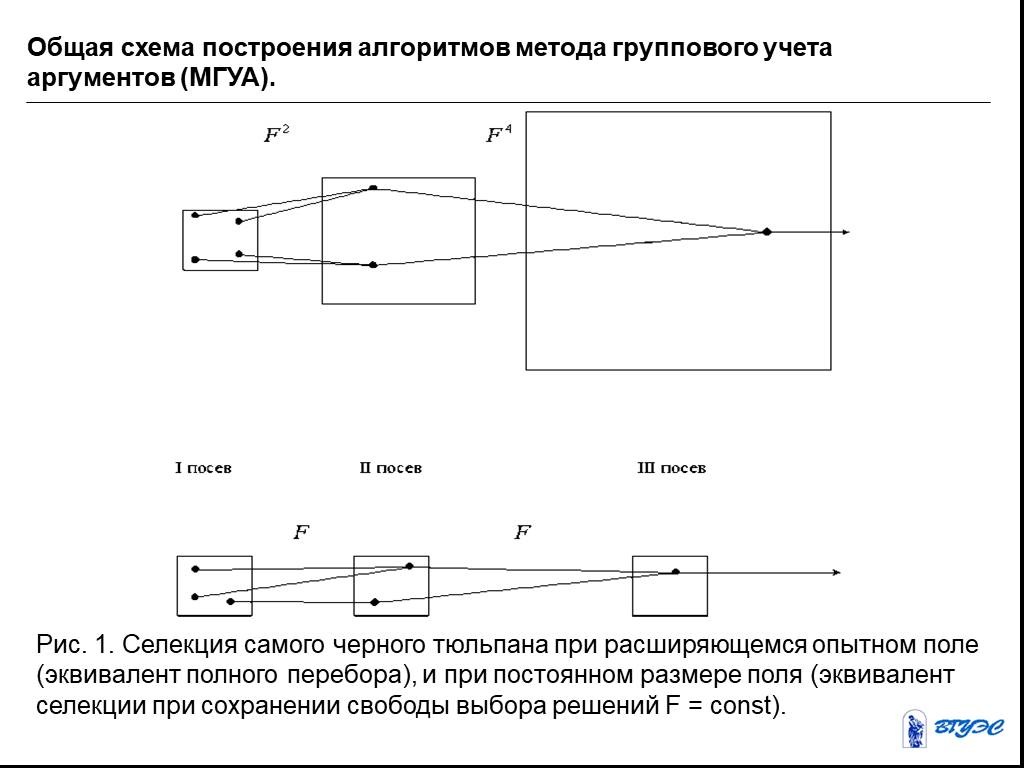












![Алгоритмы МГУА воспроизводят схему массовой селекции [Васильев В. И., Коноваленко В. В., Горелов Ю. И. Имитационное управление неопределенными объектами. // К.: “Наукова думка”, 1989—216с. ], показанной на Рис. 1. В них есть генераторы усложняющихся из ряда в ряд комбинаций и пороговые самоотборы лу Алгоритмы МГУА воспроизводят схему массовой селекции [Васильев В. И., Коноваленко В. В., Горелов Ю. И. Имитационное управление неопределенными объектами. // К.: “Наукова думка”, 1989—216с. ], показанной на Рис. 1. В них есть генераторы усложняющихся из ряда в ряд комбинаций и пороговые самоотборы лу](https://prezentacii.org/upload/cloud/19/03/132951/images/thumbs/screen8.jpg)



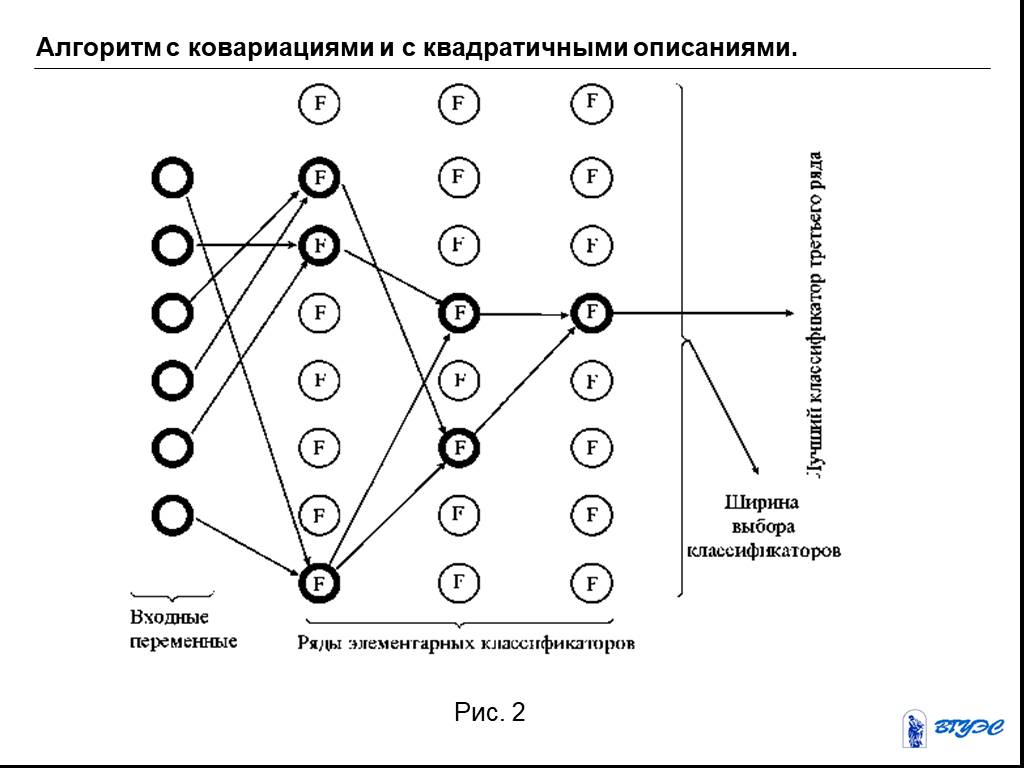
![В этом алгоритме [ Васильев В. И., Коноваленко В. В., Горелов Ю. И. Имитационное управление неопределенными объектами. // К.: “Наукова думка”, 1989—216с. , Половинкин А. И. Основы инженерного творчества. // М.: "Машиностроение", 1988—368с ] используются частные описания, представленные в с В этом алгоритме [ Васильев В. И., Коноваленко В. В., Горелов Ю. И. Имитационное управление неопределенными объектами. // К.: “Наукова думка”, 1989—216с. , Половинкин А. И. Основы инженерного творчества. // М.: "Машиностроение", 1988—368с ] используются частные описания, представленные в с](https://prezentacii.org/upload/cloud/19/03/132951/images/thumbs/screen12.jpg)































