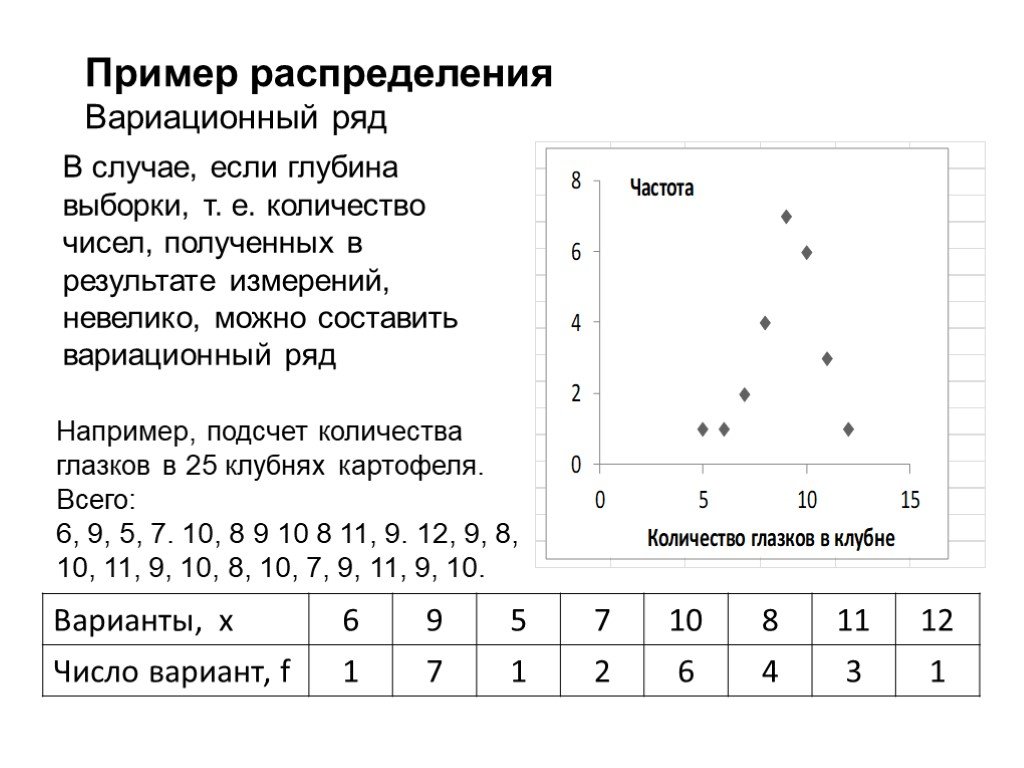
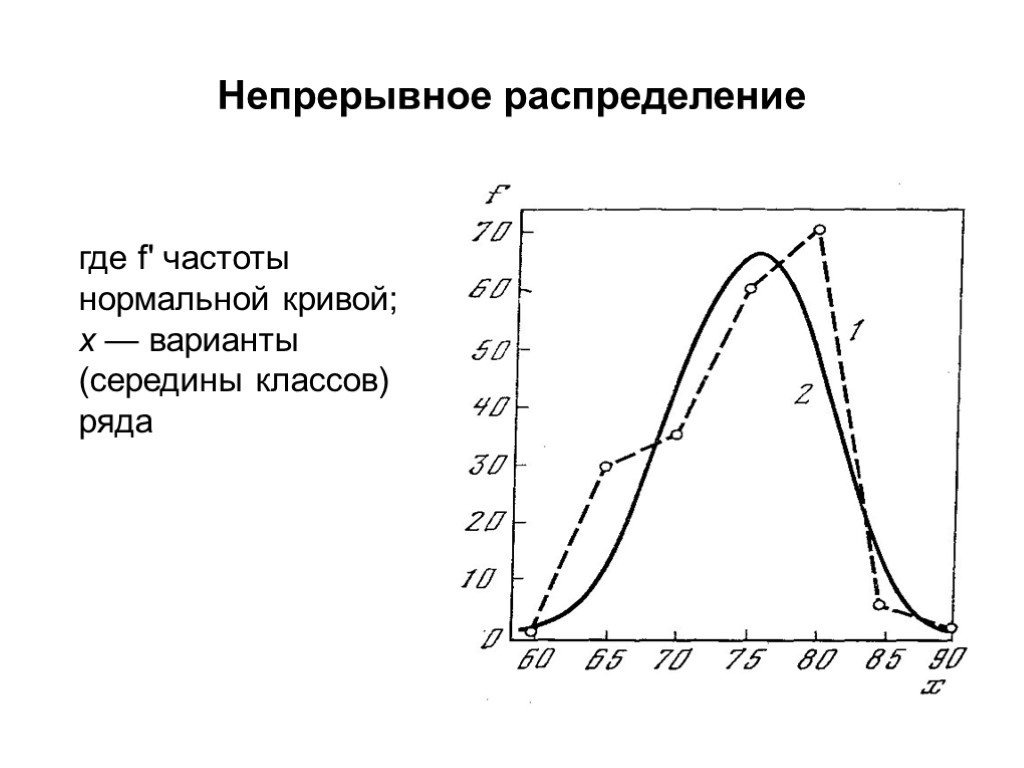
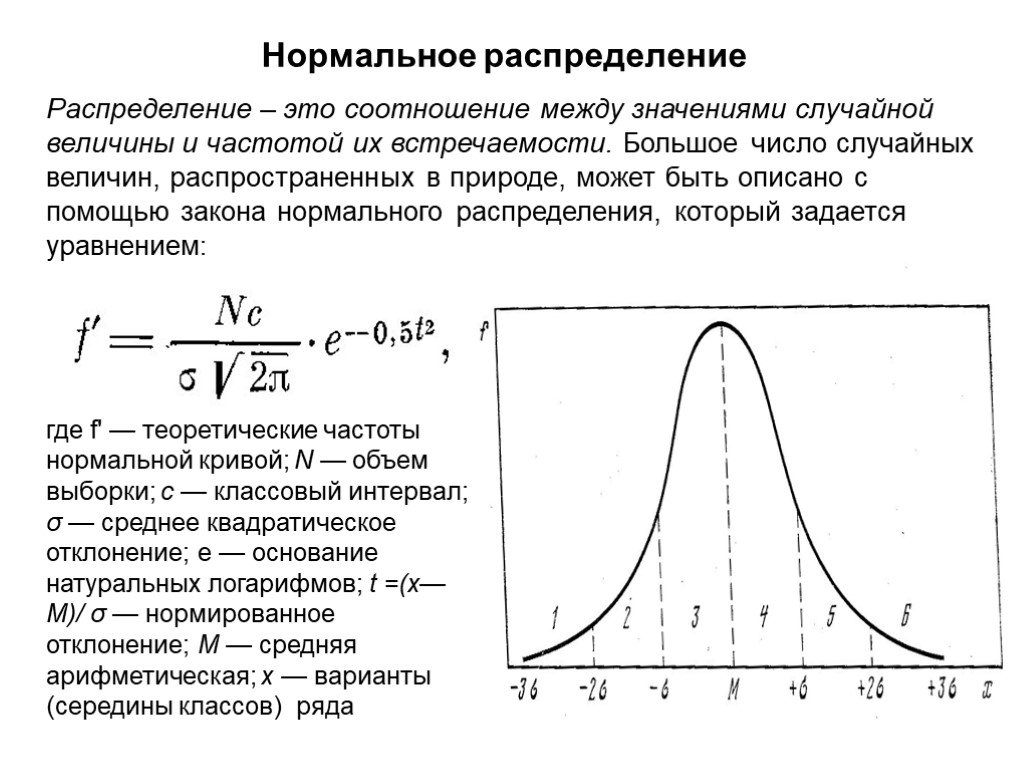
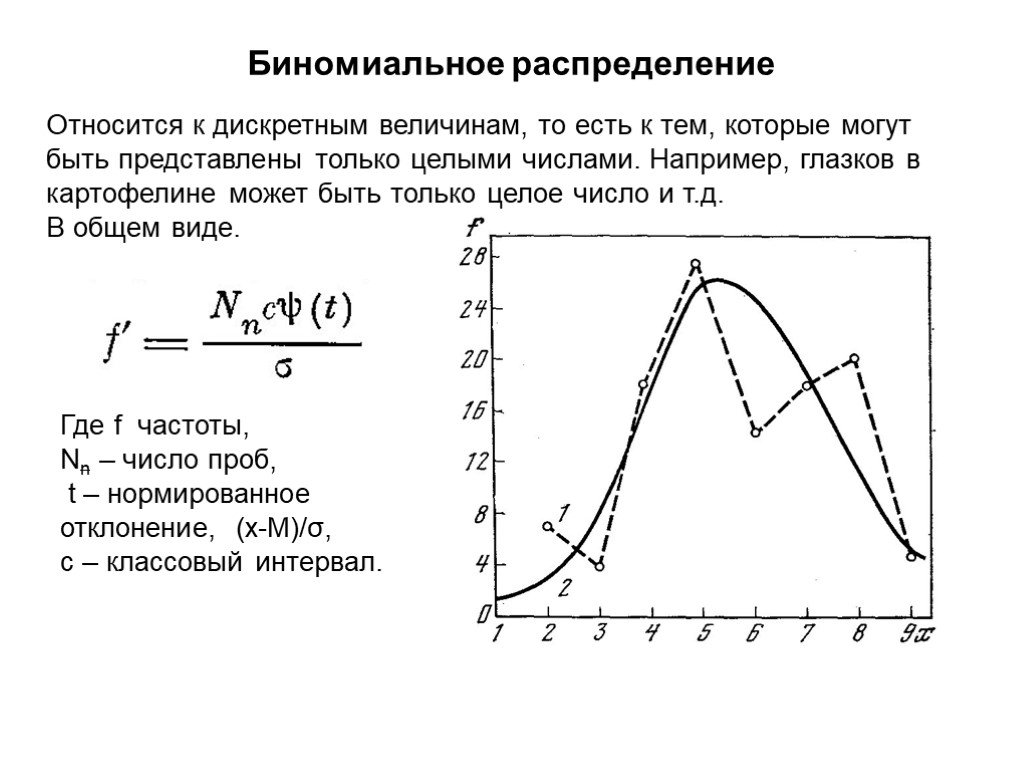
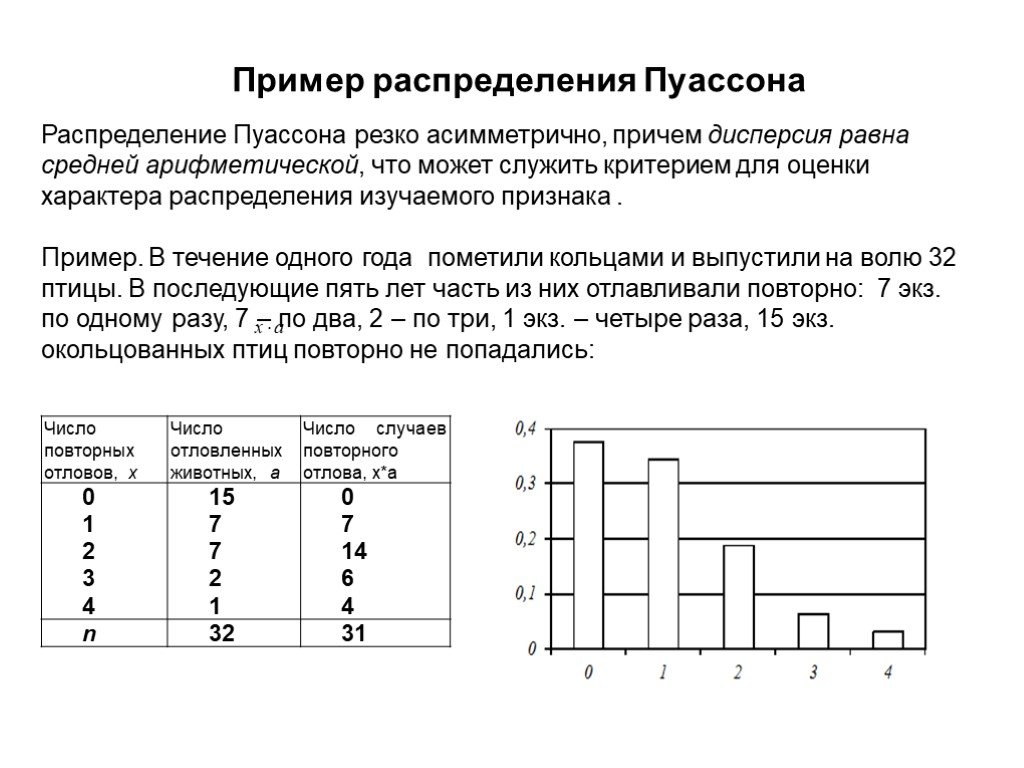
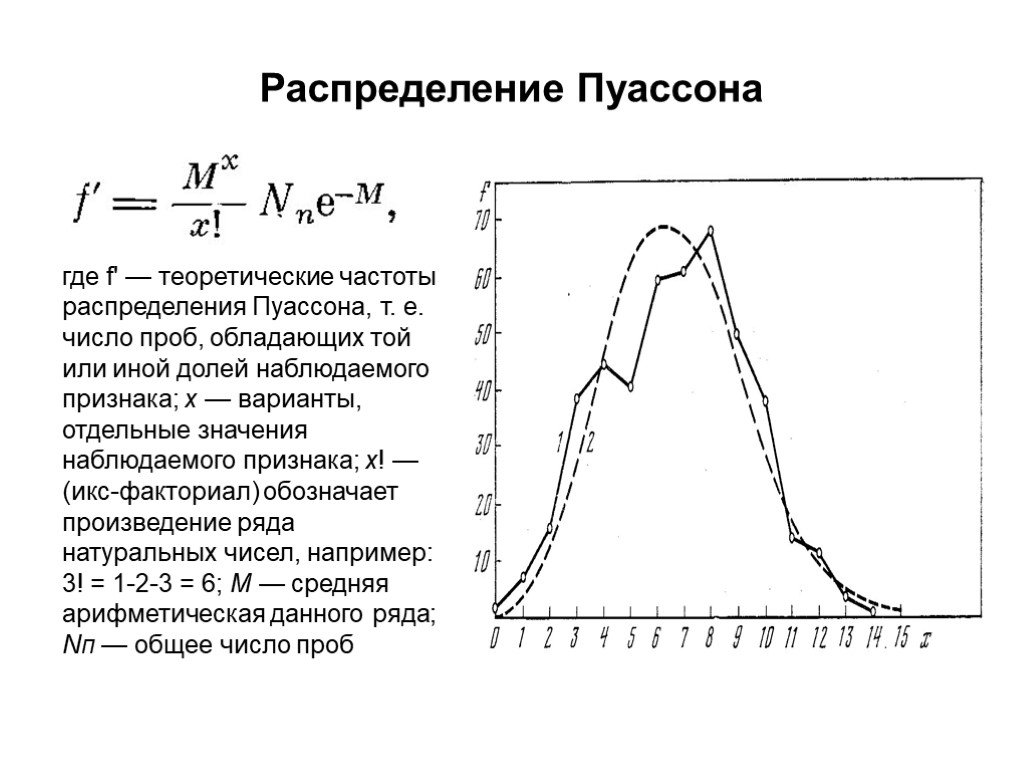
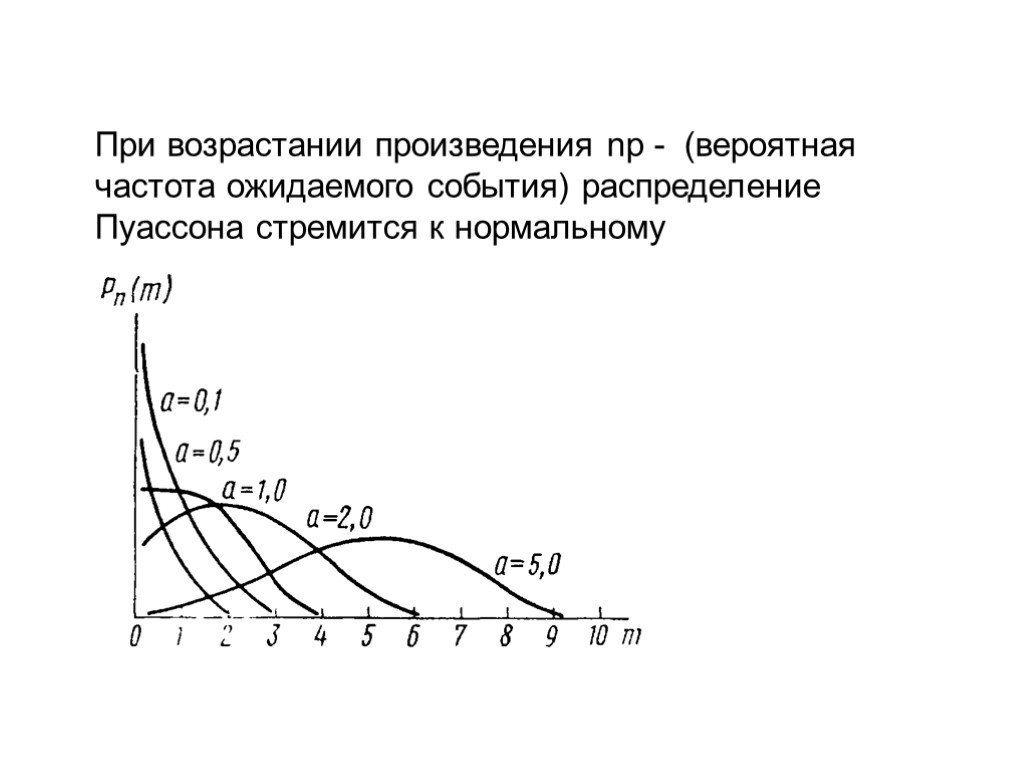
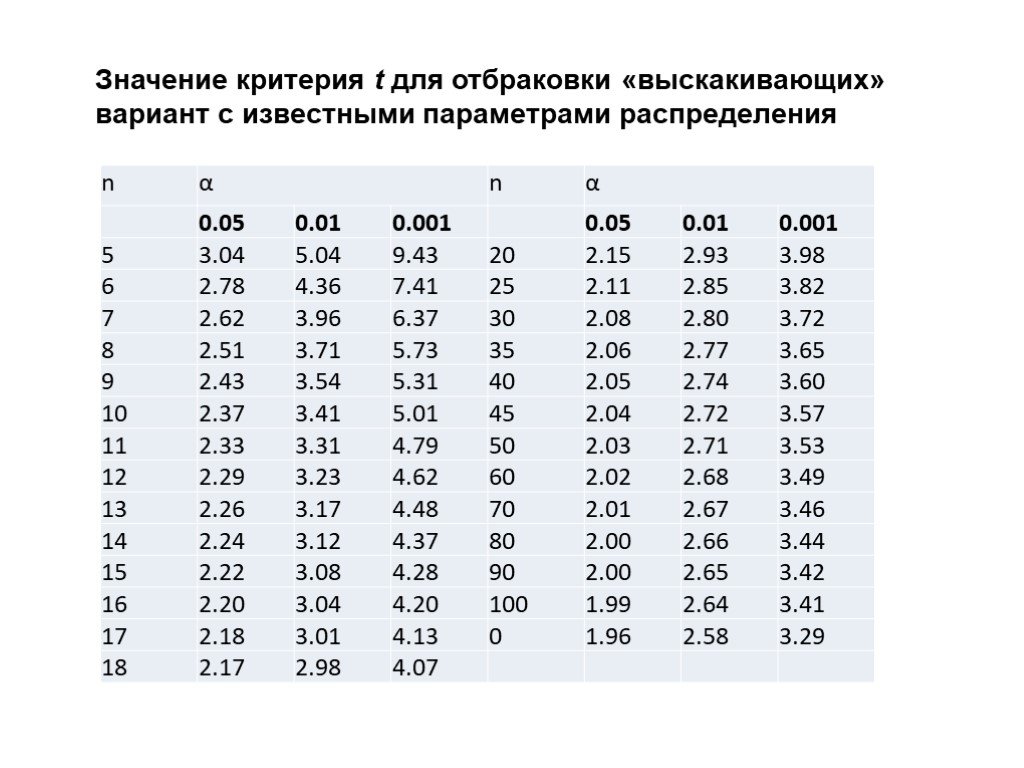
Презентация "Первичный анализ и обработка данных" по информатике – проект, доклад
Презентацию на тему "Первичный анализ и обработка данных" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 35 слайд(ов).
Слайды презентации
Список похожих презентаций
Обработка данных физического эксперимента
Введение. В настоящее время обязанности по обработке и хранению информации, не являются прерогативой исключительно научных сотрудников, так как возможности ...Обработка информации в системе управления базами данных
База данных. База данных- это совокупность взаимосвязанных и организованных определенным образом данных,отражающих состояние объектов и отношений ...Многомерный анализ данных на основе Oracle Essbase
Oracle OLAP Oracle Data Mining Oracle Partitioning Oracle Warehouse Builder. ХРАНИЛИЩА И ВИТРИНЫ ДАННЫХ. ИНСТРУМЕНТЫ БИЗНЕС-АНАЛИЗА и ОТЧЁТНОСТИ. ...Обработка данных средствами электронных таблиц Microsoft Excel
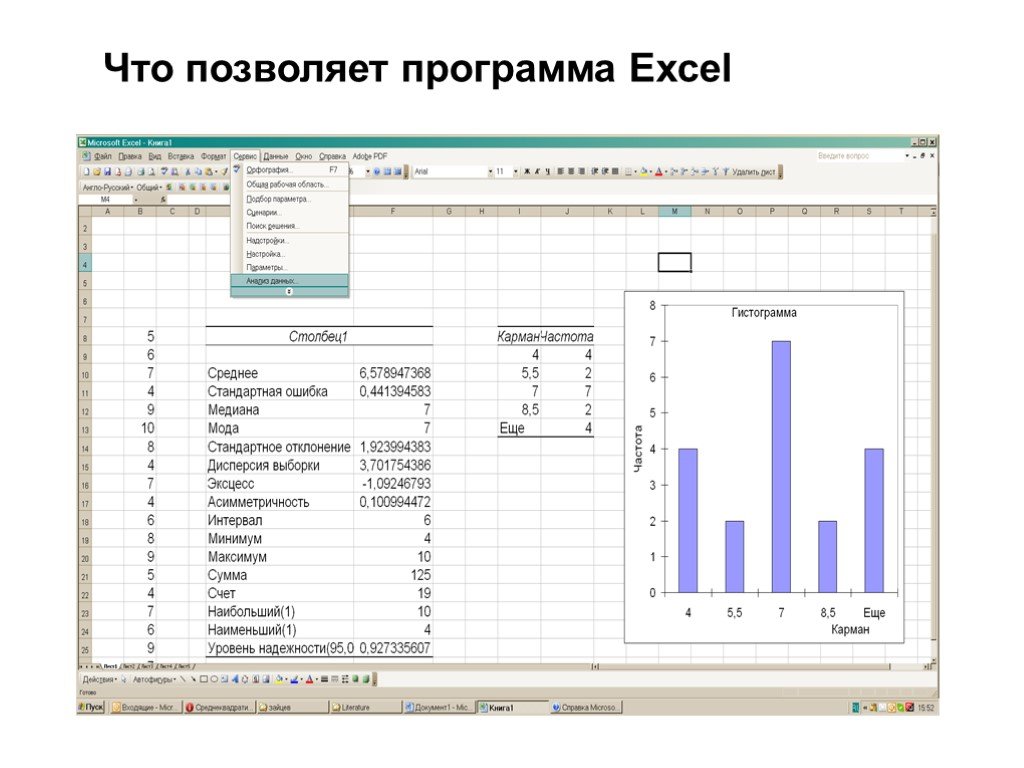
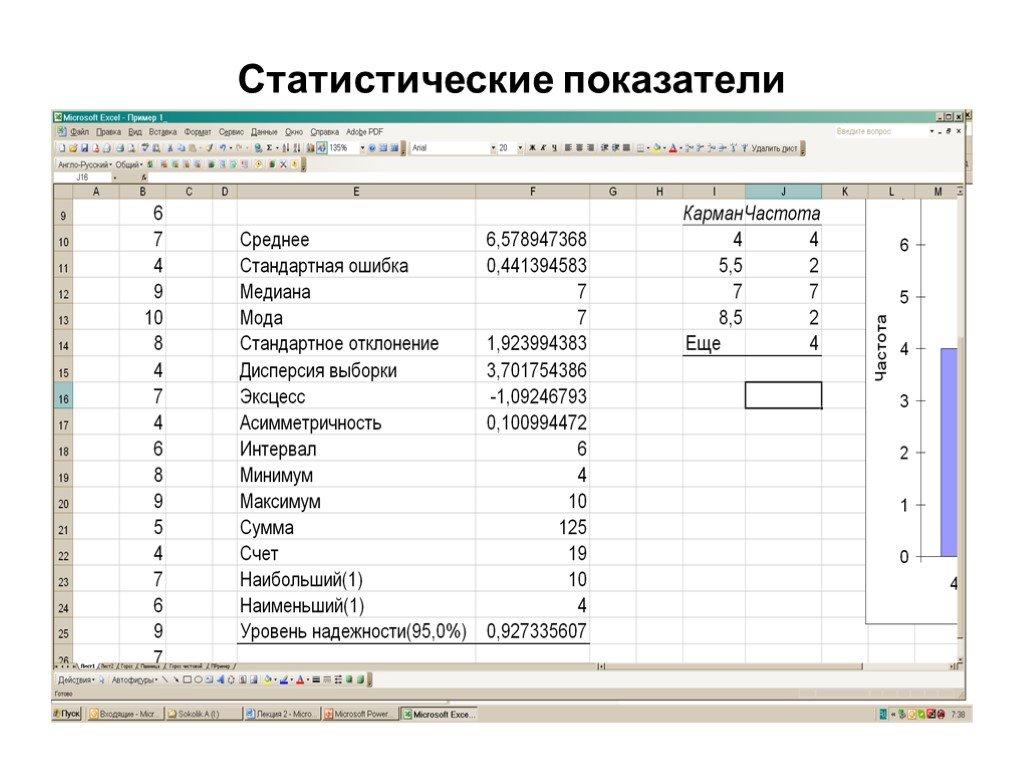
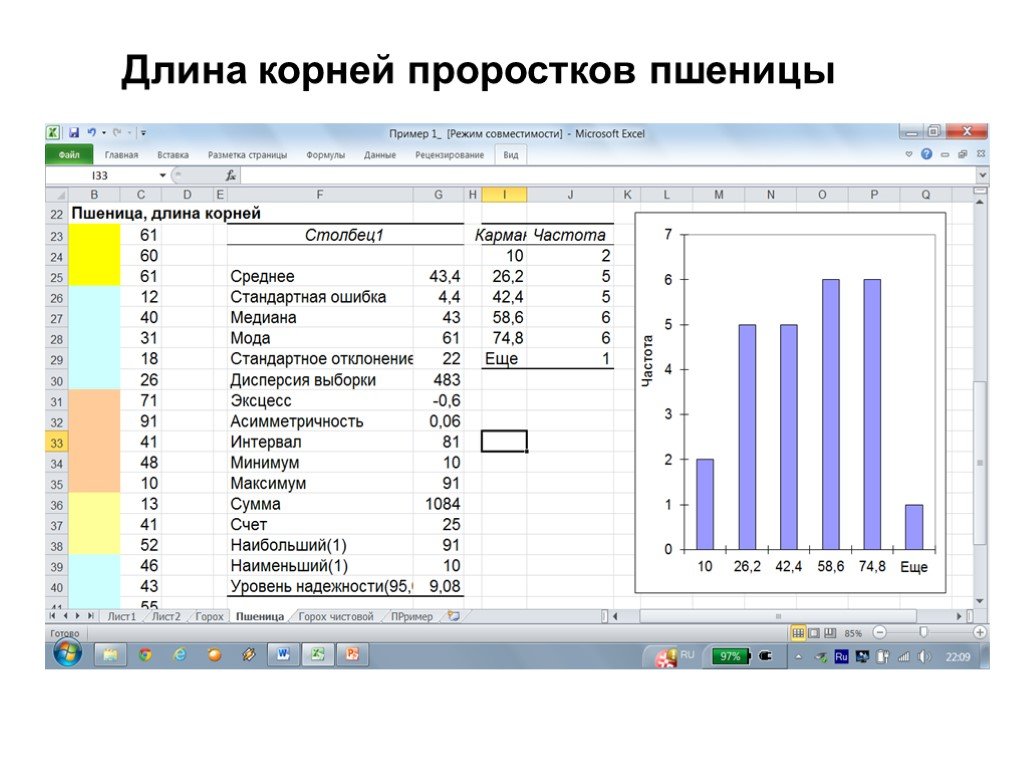
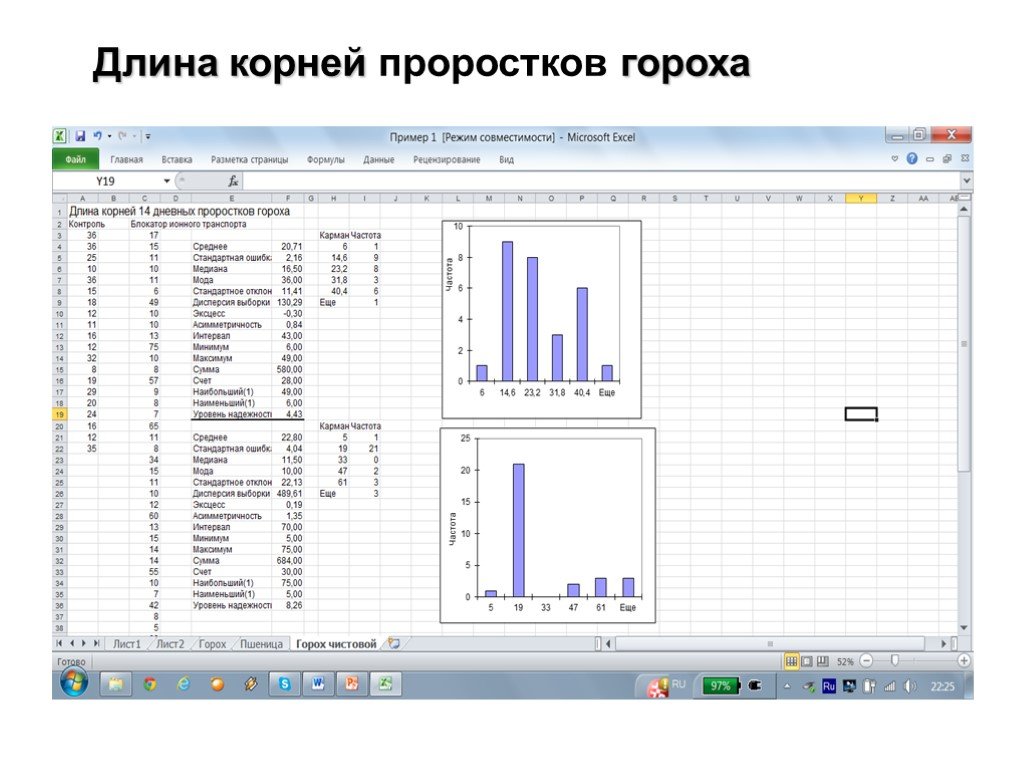
Структура интерфейса табличного процессора. Microsoft Excel – это программа управления электронными таблицами, которая используется для вычислений, ...Статистическая обработка данных в матрицах
«Скажи мне, и я забуду. Покажи мне, и я запомню. Дай действовать самому, и я пойму» Народная мудрость. Предлагаю вам ответить на следующие вопросы. ...Компьютер и обработка данных
Сегодня на уроке! Тест по теме «Передача данных» Пятиминутка «В мире новостей!» Новая тема! Физкультминутка! Закрепление изученного материала! Тест ...Программная обработка данных на компьютере
Числовая, текстовая, графическая и звуковая информация может обрабатываться компьютером, если она представлена в двоичной знаковой системе. Для обработки ...Программная обработка данных на компьютере
Программная обработка данных на компьютере. Данные – это информация (числовая, текстовая, графическая, звуковая), которая обрабатывается компьютером ...Программная обработка данных на компьютере
Основной функцией компьютера является обработка информации. 50-60-е годы – вычисление 70-е годы – работа с текстом 80-е годы – работа с графической ...Программная обработка данных на компьютере
1) Назовите типы информации. М А. 2) В виде чего информация представлена в компьютере? Двоичный код – последовательность из 8 электрических импульсов ...Графическая обработка данных в табличном процессоре MS EXCEL
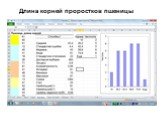
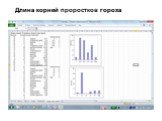
Графическое представление данных. Замечательным свойством электронных таблиц является возможность графического представления числовой информации, ...Инструментарий сбора, обработки и анализа данных для управления качеством образования на региональном и муниципальном уровнях
Функции усовершенствованной БД. сбор первичных статистических данных автоматизированный расчет индикаторов по региону в целом автоматизированный расчет ...Обработка массива данных
1. Укажите правильное расширение файлов, написанных в пакете “Excel” *.doc *.xls *.exe. 2. Какой формат числа используется для ввода даты Общий Время ...Основная микросхема компьютера, выполняющая обработку данных
Устройство для считывания информации с листа бумаги в компьютер. Устройство для ввода звуковой информации. Устройство для обмена информацией с другими ...Элементы теории проектирования баз данных и информационных систем
Цель: Содержание:. Рассмотреть современный подходы к моделированию предметных областей и построению БД: системный подход; концептуальное моделирование; ...Физическая защита данных на дисках
Организация надежной и эффективной системы архивации данных является одной из важнейших задач по обеспечению сохранности информации. Хранение архивной ...Сортировка и поиcк данных в электронных таблицах Excel
Цели урока:. Классифицировать основные способы работы с электронными таблицами. Рассмотреть некоторые дополнительные возможности табличного процессора ...Создание запроса на выборку в базе данных для настольных истем
В СУБД Access 2007 применяются различные типы запросов: на выборку, на обновление, на добавление, на удаление, перекрестный query, выполнение вычислений, ...Система управления базами данных
Ключевые слова. СУБД таблица форма запрос условие выбора отчёт. Что такое СУБД. Система управления базами данных (СУБД) - программное обеспечение ...Работа с базой данных MS Access
Цели урока: Образовательные: экспериментальным путем с использованием ПК работать в среде MS Access. научиться применять полученные теоретические ...Конспекты
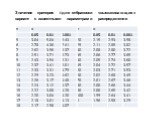
Сбор и обработка статистических данных
Урок по информатике для 11 класса (профильный уровень). Тема урока. Сбор и обработка статистических данных. Цели урока:. научиться обрабатывать ...Обработка числовой информации, средства визуализации данных
Автор Рыбакова Н.А. СОШ №44 г.Севастополь. Учитель информатики. . Открытый урок по информатике. Графические возможности Excel. . Построение ...Сбор и анализ статистических данных
Урок для 8 класса по теме. . «Сбор и анализ статистических данных». Бурякова Вера Николаевна, учитель математики ГБОУ ООШ с. Малое Ибряйкино ...База данных
Никулина Татьяна Михайловна. ГБОУ СПО «Осинский профессионально-педагогический колледж»,. преподаватель методики математики и информатики. Конспект ...Формирование сложных запросов к готовой базе данных
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №3 г.Козьмодемьянска». Конспект урока по информатике ...Архивация данных
Тема урока: Архивация данных. Цель урока:. . Сформировать понятие «архивации данных». . Ознакомить с принципами архивации. . Познакомить ...Сортировка и поиск данных в электронных таблицах
МОУ «Бендерская средняя общеобразовательная школа №13». Открытый урок. . по информатике и ИКТ. . в 9 Б классе. . по теме:. ...Табличные базы данных
Табличные базы данных. . . Тема:. Табличные базы данных. Цель урока: . формирование представления у учащихся о табличном моделировании баз ...Ввод и редактирование данных в ЭТ Excel
Муниципальное бюджетное учреждение средняя общеобразовательная школа №2. Конспект урока. По теме: «Ввод и редактирование данных в ЭТ Excel. ...Создание структуры базы данных и заполнение её данными
Муниципальное бюджетное общеобразовательное учреждение. Гимназия №19 им Поповичевой Н.З., г. Липецка. Конспект учебного занятия в 11 классах ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 января 2019
Категория:Информатика
Содержит:35 слайд(ов)
Поделись с друзьями:
Скачать презентацию